| |
Toán 10 Bài 2: Hệ bất phương trình bậc nhất hai ẩn Giải SGK Toán 10 trang 29 - Tập 1 sách Cánh diều
Bài trước
Toán 10 Cánh diều trang 29 tập 1 giúp các em học sinh có thêm nhiều gợi ý tham khảo để giải các câu hỏi Hoạt động và 4 bài tập trong SGK bài Hệ bất phương trình bậc nhất hai ẩn chính xác nhất.
Giải Toán 10 Cánh diều trang 29 tập 1 hướng dẫn giải bài tập trong sách giáo khoa rất chi tiết. Hy vọng rằng tài liệu sẽ giúp các em học sinh lớp 10 học tốt môn Toán 10. Đồng thời các thầy cô giáo, bậc phụ huynh có thể sử dụng tài liệu để hướng dẫn các em khi tự học ở nhà được thuận tiện hơn. Vậy sau đây là trọn bộ tài liệu Toán 10 trang 29 Cánh diều mời các bạn cùng theo dõi.
Toán 10 Bài 2: Hệ bất phương trình bậc nhất hai ẩn
Phần Hoạt động
Hoạt động 1 trang 25 Toán 10 tập 1
Cho hệ phương trình sau:
![]() \(\left\{ \begin{gathered}
x - y < 3\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right) \hfill \\
x + 2y > - 2\,\,\,\,\,\,\left( 2 \right) \hfill \\
\end{gathered} \right.\)
\(\left\{ \begin{gathered}
x - y < 3\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right) \hfill \\
x + 2y > - 2\,\,\,\,\,\,\left( 2 \right) \hfill \\
\end{gathered} \right.\)
a) Mỗi bất phương trình (1) và (2) có là bất phương trình bậc nhất hai ẩn không?
b) Chỉ ra một nghiệm chung của hai bất phương trình (1) và (2) trong hệ trên.
Gợi ý đáp án
a) Bất phương trình (1) và bất phương trình (2) có là bất phương trình bậc nhất hai ẩn.
b) Thay ![]() \(x = 1\) và
\(x = 1\) và ![]() \(y = 1\) vào hai bất phương trình của hệ, ta có:
\(y = 1\) vào hai bất phương trình của hệ, ta có:
+ ![]() \(1 - 1 < 3\) là mệnh đề đúng.
\(1 - 1 < 3\) là mệnh đề đúng.
+ ![]() \(1 + 2.1 > - 2\) là mệnh đề đúng.
\(1 + 2.1 > - 2\) là mệnh đề đúng.
Vậy (1; 1) là nghiệm chung của bất phương trình (1) và bất phương trình (2) nên (1; 1) là nghiệm của hệ bất phương trình.
Hoạt động 2 trang 26 Toán 10 tập 1
Cho hệ bất phương trình sau:
 \(\left\{ \begin{gathered} x - 2y \geqslant - 2 \hfill \\
7x - 4y \leqslant 16 \hfill \\
2x + y \geqslant - 4 \hfill \\
\end{gathered} \right.\)
\(\left\{ \begin{gathered} x - 2y \geqslant - 2 \hfill \\
7x - 4y \leqslant 16 \hfill \\
2x + y \geqslant - 4 \hfill \\
\end{gathered} \right.\)
a) Trong cùng mặt phẳng tọa độ Oxy, biểu diễn miền nghiệm của mỗi bất phương trình trong hệ bất phương trình bằng cách gạch bỏ phần không thuộc miền nghiệm của nó.
b) Tìm miền nghiệm của hệ bất phương trình đã cho.
Gợi ý đáp án
a) ![]() \(x - 2y \geqslant - 2\)
\(x - 2y \geqslant - 2\)
+ Vẽ đường thẳng ![]() \({d_1}:x - 2y = - 2 \Leftrightarrow y = \frac{1}{2}x + 1\)
\({d_1}:x - 2y = - 2 \Leftrightarrow y = \frac{1}{2}x + 1\)
+ Lấy điểm ![]() \(O\left( {0;0} \right)\). Ta có:
\(O\left( {0;0} \right)\). Ta có: ![]() \(0 - 2.0 = 0 \geqslant - 2\).
\(0 - 2.0 = 0 \geqslant - 2\).
+ Vậy miền nghiệm của bất phương trình ![]() \(x - 2y \geqslant - 2\) là nửa mặt phẳng không bị gạch, chứa điểm
\(x - 2y \geqslant - 2\) là nửa mặt phẳng không bị gạch, chứa điểm ![]() \(O\left( {0;0} \right)\) không kể đường thẳng
\(O\left( {0;0} \right)\) không kể đường thẳng ![]() \(y = \frac{1}{2}x + 1\).
\(y = \frac{1}{2}x + 1\).
![]() \(7x - 4y \leqslant 16\)
\(7x - 4y \leqslant 16\)
+ Vẽ đường thẳng ![]() \({d_2}:7x - 4y = 16 \Leftrightarrow y = \frac{7}{4}x - 4\)
\({d_2}:7x - 4y = 16 \Leftrightarrow y = \frac{7}{4}x - 4\)
+ Lấy điểm ![]() \(O\left( {0;0} \right)\). Ta có:
\(O\left( {0;0} \right)\). Ta có: ![]() \(7.0 - 4.0 = 0 \leqslant 16\).
\(7.0 - 4.0 = 0 \leqslant 16\).
+ Vậy miền nghiệm của bất phương trình ![]() \(7x - 4y \leqslant 16\) là nửa mặt phẳng không bị gạch, chứa điểm
\(7x - 4y \leqslant 16\) là nửa mặt phẳng không bị gạch, chứa điểm ![]() \(O\left( {0;0} \right)\), kể cả đường thẳng
\(O\left( {0;0} \right)\), kể cả đường thẳng ![]() \(y = \frac{7}{4}x - 4\).
\(y = \frac{7}{4}x - 4\).
![]() \(2x + y \geqslant - 4\)
\(2x + y \geqslant - 4\)
+ Vẽ đường thẳng ![]() \({d_3}:2x + y = - 4 \Leftrightarrow y = - 2x - 4\)
\({d_3}:2x + y = - 4 \Leftrightarrow y = - 2x - 4\)
+ Lấy điểm ![]() \(O\left( {0;0} \right)\). Ta có:
\(O\left( {0;0} \right)\). Ta có: ![]() \({d_3}:2x + y = - 4 \Leftrightarrow y = - 2x - 4\).
\({d_3}:2x + y = - 4 \Leftrightarrow y = - 2x - 4\).
+ Vậy miền nghiệm của bất phương trình ![]() \(2x + y \geqslant - 4\) là nửa mặt phẳng không bị gạch, chứa điểm
\(2x + y \geqslant - 4\) là nửa mặt phẳng không bị gạch, chứa điểm ![]() \(O\left( {0;0} \right)\), kể cả đường thẳng
\(O\left( {0;0} \right)\), kể cả đường thẳng ![]() \(y = - 2x - 4\).
\(y = - 2x - 4\).
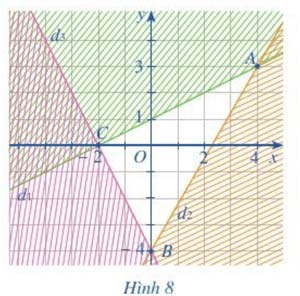
b) Phần không bị gạch (chứa điểm ) là miền nghiệm của hệ bất phương trình đã cho do tọa độ điểm thỏa mãn các bất phương trình trong hệ.
Phần Bài tập
Bài 1 trang 29 Toán 10 Cánh diều
Kiểm tra xem mỗi cặp số (x;y) đã cho có là nghiệm của hệ bất phương trình tương ứng không.
![]() \(a) \left\{ \begin{array}{l}3x + 2y \ge - 6\\x + 4y > 4\end{array} \right. \left( {0;2} \right),\left( {1;0} \right)\)
\(a) \left\{ \begin{array}{l}3x + 2y \ge - 6\\x + 4y > 4\end{array} \right. \left( {0;2} \right),\left( {1;0} \right)\)
![]() \(b) \left\{ \begin{array}{l}4x + y \le - 3\\ - 3x + 5y \ge - 12\end{array} \right. \left( { - 1; - 3} \right),\left( {0; - 3} \right)\)
\(b) \left\{ \begin{array}{l}4x + y \le - 3\\ - 3x + 5y \ge - 12\end{array} \right. \left( { - 1; - 3} \right),\left( {0; - 3} \right)\)
Gợi ý đáp án
a) Thay x = 0,y = 2 vào hệ ![]() \(\left\{ \begin{array}{l}3x + 2y \ge - 6\\x + 4y > 4\end{array} \right.\) ta được:
\(\left\{ \begin{array}{l}3x + 2y \ge - 6\\x + 4y > 4\end{array} \right.\) ta được:
![]() \(\left\{ \begin{array}{l}3.0 + 2.2 \ge - 6\\0 + 4.2 > 4\end{array} \right.\) (Đúng)
\(\left\{ \begin{array}{l}3.0 + 2.2 \ge - 6\\0 + 4.2 > 4\end{array} \right.\) (Đúng)
Thay x = 1,y = 0 vào hệ ![]() \(\left\{ \begin{array}{l}3x + 2y \ge - 6\\x + 4y > 4\end{array} \right.\) ta được:
\(\left\{ \begin{array}{l}3x + 2y \ge - 6\\x + 4y > 4\end{array} \right.\) ta được:
![]() \(\left\{ \begin{array}{l}3.1 + 2.0 \ge - 6\\1 + 4.0 > 4\left( {Sai} \right)\end{array} \right.\)
\(\left\{ \begin{array}{l}3.1 + 2.0 \ge - 6\\1 + 4.0 > 4\left( {Sai} \right)\end{array} \right.\)
Vậy ![]() \(\left( {0;2} \right)\) là nghiệm của hệ còn
\(\left( {0;2} \right)\) là nghiệm của hệ còn ![]() \(\left( {1;0} \right)\) không là nghiệm.
\(\left( {1;0} \right)\) không là nghiệm.
b) Thay x = - 1,y = - 3 vào hệ ![]() \(\left\{ \begin{array}{l}4x + y \le - 3\\ - 3x + 5y \ge - 12\end{array} \right.\) ta được:
\(\left\{ \begin{array}{l}4x + y \le - 3\\ - 3x + 5y \ge - 12\end{array} \right.\) ta được:
 \(\left\{ \begin{array}{l}4.\left( { - 1} \right) + \left( { - 3} \right) \le - 3\\ - 3\left( { - 1} \right) + 5.\left( { - 3} \right) \ge - 12\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 7 \le - 3\\ - 12 \ge - 12\end{array} \right.\) (Đúng)
\(\left\{ \begin{array}{l}4.\left( { - 1} \right) + \left( { - 3} \right) \le - 3\\ - 3\left( { - 1} \right) + 5.\left( { - 3} \right) \ge - 12\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 7 \le - 3\\ - 12 \ge - 12\end{array} \right.\) (Đúng)
Thay x = 0,y = - 3 vào hệ ![]() \(\left\{ \begin{array}{l}4x + y \le - 3\\ - 3x + 5y \ge - 12\end{array} \right.\) ta được:
\(\left\{ \begin{array}{l}4x + y \le - 3\\ - 3x + 5y \ge - 12\end{array} \right.\) ta được:
 \(\left\{ \begin{array}{l}4.0 + \left( { - 3} \right) \le - 3\\ - 3.0 + 5.\left( { - 3} \right) \ge - 12\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 3 \le - 3\\ - 15 \ge - 12\left( {Sai} \right)\end{array} \right.\)
\(\left\{ \begin{array}{l}4.0 + \left( { - 3} \right) \le - 3\\ - 3.0 + 5.\left( { - 3} \right) \ge - 12\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 3 \le - 3\\ - 15 \ge - 12\left( {Sai} \right)\end{array} \right.\)
Vậy ![]() \(\left( { - 1; - 3} \right)\) là nghiệm của hệ còn
\(\left( { - 1; - 3} \right)\) là nghiệm của hệ còn ![]() \(\left( {0; - 3} \right)\) không là nghiệm.
\(\left( {0; - 3} \right)\) không là nghiệm.
Bài 2 trang 29 Toán 10 Cánh diều
Biểu diễn miền nghiệm của hệ bất phương trình:
![]() \(a) \left\{ \begin{array}{l}x + 2y < - 4\\y \ge x + 5\end{array} \right.\)
\(a) \left\{ \begin{array}{l}x + 2y < - 4\\y \ge x + 5\end{array} \right.\)
 \(b) \left\{ \begin{array}{l}4x - 2y > 8\\x \ge 0\\y \le 0\end{array} \right.\)
\(b) \left\{ \begin{array}{l}4x - 2y > 8\\x \ge 0\\y \le 0\end{array} \right.\)
Gợi ý đáp án
a) Vẽ các đường thẳng x + 2y = - 4(nét đứt) và y = x + 5 (nét liền)
Thay tọa độ O vào x + 2y < - 4 ta được: 0 + 2.0 < - 4 (Sai)
=> Gạch đi phần chứa O.
Thay tọa độ O vào ![]() \(y \ge x + 5\) ta được:
\(y \ge x + 5\) ta được: ![]() \(0 \ge 0 + 5\) (Sai)
\(0 \ge 0 + 5\) (Sai)
=> Gạch đi phần chứa O.
Miền nghiệm của hệ:
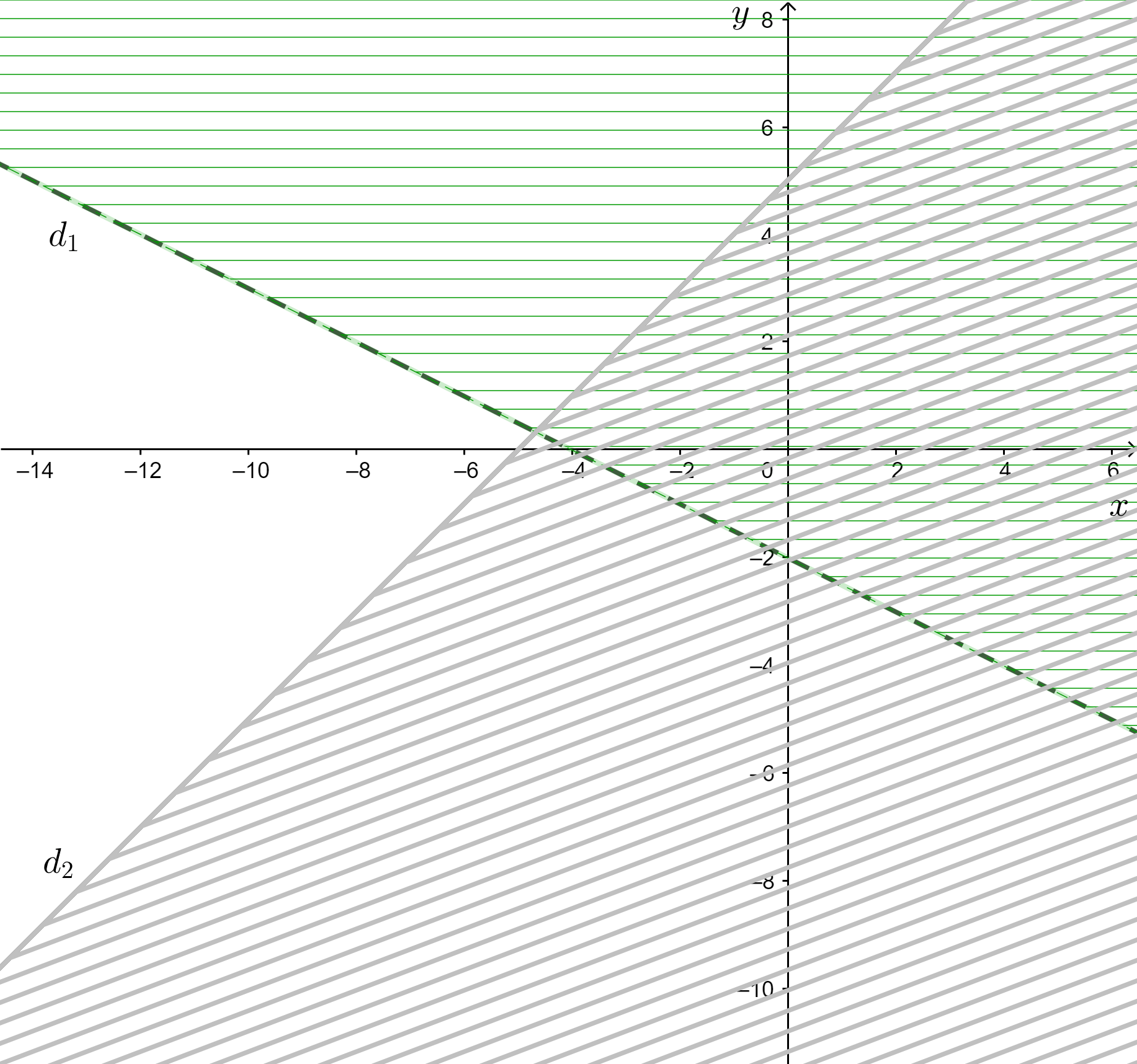
Từ hình vẽ ta thấy hệ vô nghiệm.
b) Vẽ các đường thẳng 4x - 2y = 8 (nét đứt) và hai trục (nét liền)
Thay tọa độ O vào 4x - 2y > 8 ta được: 4.0 - 2.0 > 8 (Sai)
=> Gạch đi phần chứa O.
Với ![]() \(x \ge 0\) thì gạch phần bên trái Oy
\(x \ge 0\) thì gạch phần bên trái Oy
Với ![]() \(y \le 0\) thì gạch bên trên Ox
\(y \le 0\) thì gạch bên trên Ox
Miền nghiệm của hệ:
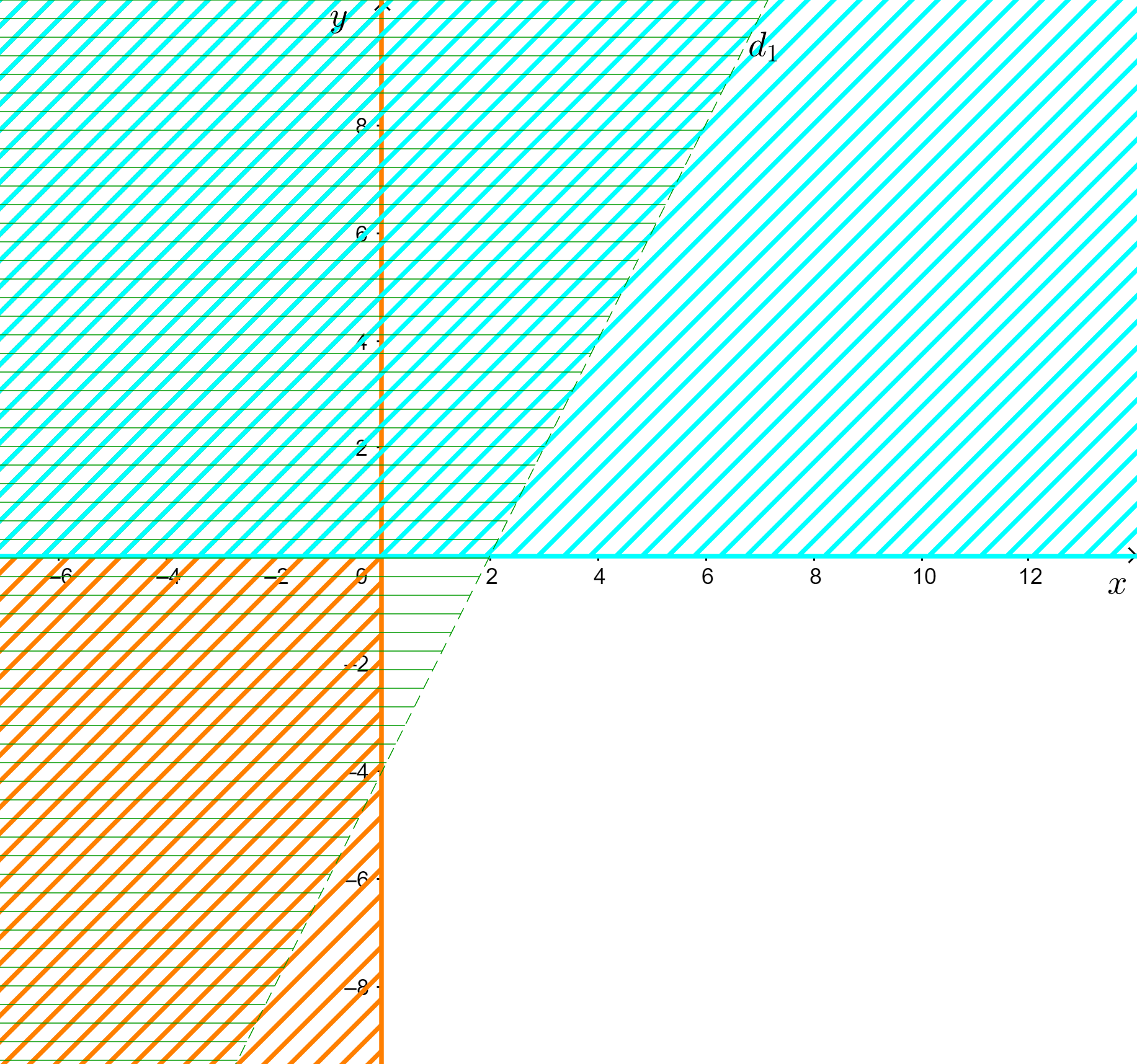
Bài 3 trang 29 Toán 10 Cánh diều
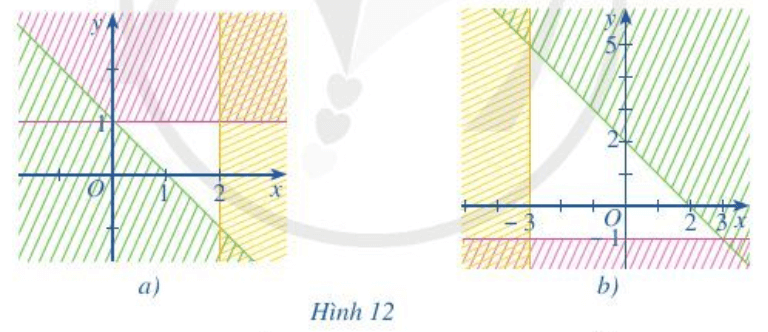
Miền không bị gạch ở mỗi Hình 12a, 12b là miền nghiệm của hệ bất phương trình nào cho ở dưới đây?
 \(\left\{ \begin{array}{l}x + y < 2\\x > - 3\\y \ge - 1\end{array} \right.\) \(\left\{ \begin{array}{l}x + y < 2\\x > - 3\\y \ge - 1\end{array} \right.\) |
 \(b) \left\{ \begin{array}{l}y < x\\x \le 0\\y > - 3\end{array} \right.\) \(b) \left\{ \begin{array}{l}y < x\\x \le 0\\y > - 3\end{array} \right.\) |
 \(c) \left\{ \begin{array}{l}y > - x + 1\\x \le 2\\y < 1\end{array} \right.\) \(c) \left\{ \begin{array}{l}y > - x + 1\\x \le 2\\y < 1\end{array} \right.\) |
Gợi ý đáp án
Hình 12a
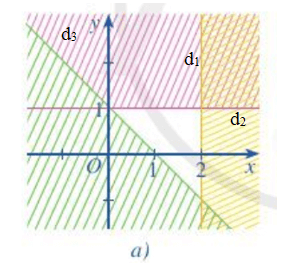
Ta thấy các đường thẳng trên hình là y = 1;x = 2;y = - x + 1
Từ các phương trình trên thì ta chọn luôn là câu c mà không cần xét tiếp.
Hình 12b.
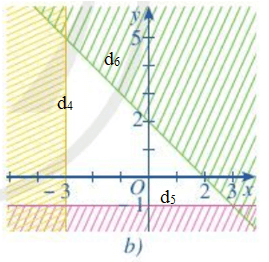
Ta thấy các đường thẳng trên hình là y = - 1;x = - 3;x + y = - 2
Từ các phương trình trên thì ta chọn luôn là câu a mà không cần xét tiếp
Bài 4 trang 29 Toán 10 Cánh diều
Một phân xưởng sản xuất hai kiểu mũ. Thời gian để làm ra một chiếc mũ kiểu thứ nhất nhiều gấp hai lần thời gian làm ra một chiếc mũ kiểu thứ hai. Nếu chỉ sản xuất toàn kiểu mũ thứ hai thì trong 1 giờ phân xưởng làm được 60 chiếc. Phân xưởng làm việc 8 tiếng mỗi ngày và thị trường tiêu thụ tối đa trong một ngày là 200 chiếc mũ kiểu thứ nhất và 240 chiếc mũ kiểu thứ hai. Tiền lãi khi bán một chiếc mũ kiểu thứ nhất là 24 nghìn đồng, một chiếc mũ kiểu thứ hai là 15 nghìn đồng. Tính số lượng mũ kiểu thứ nhất và kiểu thứ hai trong một ngày mà phân xưởng cần sản xuất để tiền lãi thu được là cao nhất.
Gợi ý đáp án
Bước 1: Gọi số lượng mũ kiểu thứ nhất và kiểu thứ hai trong một ngày mà phân xưởng cần sản xuất lần lượt là x và y ![]() \(\left( {x,y \in \mathbb{N}} \right)\). Biểu diễn các đại lượng khác theo x và y.
\(\left( {x,y \in \mathbb{N}} \right)\). Biểu diễn các đại lượng khác theo x và y.
Gọi số lượng mũ kiểu thứ nhất và kiểu thứ hai trong một ngày mà phân xưởng cần sản xuất lần lượt là x và ![]() \(y \left( {x,y \in \mathbb{N}} \right).\)
\(y \left( {x,y \in \mathbb{N}} \right).\)
Theo giả thiết, thị trường tiêu thụ tối đa trong một ngày là 200 chiếc mũ kiểu thứ nhất và 240 chiếc mũ kiểu thứ hai nên ta có ![]() \(0 \le x \le 200;0 \le y \le 240\)
\(0 \le x \le 200;0 \le y \le 240\)
Thời gian làm y chiếc kiểu 2 trong một ngày là ![]() \(\frac{y}{{60}}\left( h \right)\)
\(\frac{y}{{60}}\left( h \right)\)
Thời gian để làm ra một chiếc mũ kiểu thứ nhất nhiều gấp hai lần thời gian làm ra một chiếc mũ kiểu thứ hai nên thời gian làm mũ thứ nhất là 1 giờ làm được 30 chiếc.
Thời gian làm x chiếc kiểu 1 trong một ngày là ![]() \(\frac{x}{{30}}\left( h \right)\)
\(\frac{x}{{30}}\left( h \right)\)
Tổng thời gian làm trong một ngày là 8h nên ta có:
![]() \(\frac{x}{{30}} + \frac{y}{{60}} = 8\)
\(\frac{x}{{30}} + \frac{y}{{60}} = 8\)
Bước 2: Lập hệ bất phương trình.
Bước 3: Biểu diễn miền nghiệm.
Miền biểu diễn miền nghiệm là phần màu vàng:
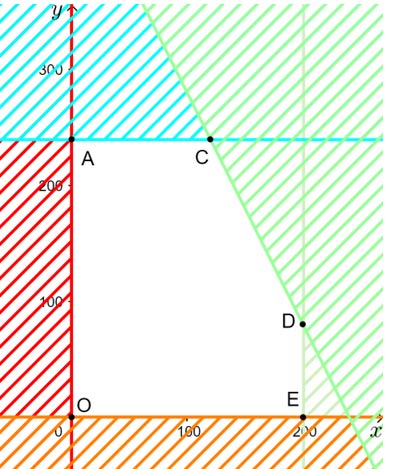
Bước 4: Tìm x và y để tiền lãi cao nhất.
Từ miền nghiệm ta thấy tiền lãi cao nhất tại khi điểm \left( {x;y} \right) là một trong các đỉnh của tam giác màu vàng:
T = 24x + 15y
![]() \(T\left( {0;240} \right) = 15.240 = 3600\) (nghìn đồng)
\(T\left( {0;240} \right) = 15.240 = 3600\) (nghìn đồng)
![]() \(T\left( {120;0} \right) = 24.120 = 2880\) (nghìn đồng)
\(T\left( {120;0} \right) = 24.120 = 2880\) (nghìn đồng)
Số lượng mũ kiểu 1 là 240 và số lượng mũ kiểu 2 là 0
Liên kết tải về
Toán 10 Bài 2: Hệ bất phương trình bậc nhất hai ẩn
723,9 KB
Tải về
Xác thực tài khoản!
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
Số điện thoại chưa đúng định dạng!
Sắp xếp theo
Chủ đề liên quan
Tìm bài trong mục này
Đóng
Chỉ thành viên Download Pro tải được nội dung này!
Download Pro - Tải nhanh, website không quảng cáo!
Tìm hiểu thêm












 Toán 10 Kết nối tri thức
Toán 10 Kết nối tri thức
 Toán 10 Chân trời sáng tạo
Toán 10 Chân trời sáng tạo
 Toán 10 Cánh Diều
Toán 10 Cánh Diều
 Soạn văn 10 Chân trời sáng tạo
Soạn văn 10 Chân trời sáng tạo
 Soạn văn 10 Cánh Diều
Soạn văn 10 Cánh Diều
 Soạn văn 10 Kết nối tri thức
Soạn văn 10 Kết nối tri thức
 Tiếng Anh 10 Global Success
Tiếng Anh 10 Global Success
 Tiếng anh 10 Friends Global
Tiếng anh 10 Friends Global
 Tiếng Anh 10 Explore New Worlds
Tiếng Anh 10 Explore New Worlds









