Toán 10 Bài 1: Giá trị lượng giác của một góc từ 0 độ đến 180 độ. Định lý côsin và định lý sin trong tam giác Giải SGK Toán 10 trang 71 - Tập 1 sách Cánh diều

Bài trước

Mục lục

Bài sau

Toán 10 Chân trời sáng tạo trang 71 giúp các em học sinh có thêm nhiều gợi ý tham khảo để giải các câu hỏi phần khởi động, luyện tập và 8 bài tập cuối bài Giá trị lượng giác của một góc từ 0 đến 180 - Định lí cosin và định lí sin trong tam giác được nhanh chóng và dễ dàng hơn.

Giải Toán 10 Cánh diều tập 1 trang 71 hướng dẫn giải bài tập trong sách giáo khoa rất chi tiết. Hy vọng rằng tài liệu sẽ giúp các em học sinh học tốt môn Toán 10. Đồng thời các thầy cô giáo, bậc phụ huynh có thể sử dụng tài liệu để hướng dẫn các em khi tự học ở nhà được thuận tiện hơn. Vậy sau đây là trọn bộ tài liệu giải Toán 10 trang 71 Cánh diều mời các bạn cùng theo dõi.

Toán 10 Bài 1: Giá trị lượng giác của một góc từ 0 độ đến 180 độ

Phần Khởi động

Cột cờ Lũng Cú là cột cờ Quốc gia, nằm ở đỉnh Lũng Cú hay còn gọi là đỉnh núi Rồng (Long Sơn) thuộc xã Lũng Cú, huyện Đồng Văn, tỉnh Hà Giang, cách cực Bắc Việt Nam khoảng 3,3 km. ....

Gợi ý đáp án

a có: $\mathrm{Bx} / / \mathrm{CH} \Rightarrow \widehat{B C H}=\widehat{x B C}=50^{\circ}$ $\mathrm{Bx} / / \mathrm{CH} \Rightarrow \widehat{B C H}=\widehat{x B C}=50^{\circ}$ (hai góc so le trong)

$\mathrm{Ay} / / \mathrm{CH} \Rightarrow \widehat{A C H}=\widehat{y A C}=45$ $\mathrm{Ay} / / \mathrm{CH} \Rightarrow \widehat{A C H}=\widehat{y A C}=45$ (hai góc so le trong)

Tam giác ACH vuông tại H có $\widehat{A C H}=45^{\circ}$ $\widehat{A C H}=45^{\circ}$nên tam giác ACH vuông cân tại H

Suy ra CH = AH = h (m).

Ta có: BH = AB + AH = 20,25 + h

Tam giác BCH vuông tại H nên $\widehat{B C H}=\frac{B H}{C H}$ $\widehat{B C H}=\frac{B H}{C H}$

Do đó ta có: $\frac{20,25+h}{h}=\tan 50^{\circ} \approx 1,2$ $\frac{20,25+h}{h}=\tan 50^{\circ} \approx 1,2$

⇒ 20,25 + h = 1,2h

⇒ 0,2h = 20,25 ⇒ h = 101,25 m.

Vậy chiều cao h của đỉnh Lũng Cú so với chân núi là 101,25 m.

Phần Luyện tập

Luyện tập 1 trang 66 Toán 10 tập 1

Hãy tính chiều cao h của đỉnh Lũng Cú so với chân núi trong bài toán ở phần mở đầu.

Gợi ý đáp án

$\left\{ \begin{array}{l}\widehat {ACH} = {45^o}\\\widehat {BCH} = {50^o}\end{array} \right.$ $\left\{ \begin{array}{l}\widehat {ACH} = {45^o}\\\widehat {BCH} = {50^o}\end{array} \right.$. (hai góc đồng vị)

Mà $\tan \widehat {ACH} = \frac{{AH}}{{CH}} \Rightarrow \tan {45^o} = \frac{h}{{CH}} \Leftrightarrow CH = h$ $\tan \widehat {ACH} = \frac{{AH}}{{CH}} \Rightarrow \tan {45^o} = \frac{h}{{CH}} \Leftrightarrow CH = h$

Lại có: $\tan \widehat {BCH} = \frac{{BH}}{{CH}} \Rightarrow \tan {50^o} = \frac{{h + 20,25}}{h}$ $\tan \widehat {BCH} = \frac{{BH}}{{CH}} \Rightarrow \tan {50^o} = \frac{{h + 20,25}}{h}$

$\begin{array}{l} \Leftrightarrow h.\tan {50^o} = h + 20,25\\ \Leftrightarrow h = \frac{{20,25}}{{\tan {{50}^o} - 1}} \approx 105,6\end{array}$ $\begin{array}{l} \Leftrightarrow h.\tan {50^o} = h + 20,25\\ \Leftrightarrow h = \frac{{20,25}}{{\tan {{50}^o} - 1}} \approx 105,6\end{array}$

Vậy chiều cao của đỉnh Lũng cú so với chân núi là khoảng 105,6m.

Luyện tập 2 trang 68 Toán 10 tập 1

Cho tam giác ABC có AB = 5, AC = 6, BC =7. Tính cosA.

Gợi ý đáp án

Áp dụng định lí cosin trong tam giác ABC ta có:

${a^2} = {b^2} + {c^2} - 2bc.\cos A \Rightarrow \cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}$ ${a^2} = {b^2} + {c^2} - 2bc.\cos A \Rightarrow \cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}$

Mà $AB = c = 5,{\rm{ }}AC = b = 6,{\rm{ }}BC = a = 7.$ $AB = c = 5,{\rm{ }}AC = b = 6,{\rm{ }}BC = a = 7.$

$\Rightarrow \cos A = \frac{{{6^2} + {5^2} - {7^2}}}{{2.5.6}} = \frac{1}{5}$ $\Rightarrow \cos A = \frac{{{6^2} + {5^2} - {7^2}}}{{2.5.6}} = \frac{1}{5}$

Chú ý

Từ định lí cosin, ta suy cách tìm góc khi biết độ dài 3 cạnh

Luyện tập 3 trang 70 Toán 10 tập 1

Cho tam giác ABC nội tiếp đường tròn (O) có bán kính R = 6 và có các góc $\widehat B = {65^o},\widehat C = {85^o}$ $\widehat B = {65^o},\widehat C = {85^o}$ . Tính độ dài cạnh BC.

Gợi ý đáp án

Ta có: $\widehat B = {65^o},\widehat C = {85^o}.$ $\widehat B = {65^o},\widehat C = {85^o}.$

$\Rightarrow \widehat A = {180^o} - \left( {{{65}^o} + {{85}^o}} \right) = {30^o}.$ $\Rightarrow \widehat A = {180^o} - \left( {{{65}^o} + {{85}^o}} \right) = {30^o}.$

Áp dụng định lí sin trong tam giác ABC, ta có:

$\frac{{BC}}{{\sin A}} = 2R \Rightarrow BC = 2R.\sin A$ $\frac{{BC}}{{\sin A}} = 2R \Rightarrow BC = 2R.\sin A$

Mà $\widehat A = {30^o},R = 6.$ $\widehat A = {30^o},R = 6.$

$\Rightarrow BC = 2.6.\sin {30^o} = 6.$ $\Rightarrow BC = 2.6.\sin {30^o} = 6.$

Vậy BC = 6.

Phần Bài tập

Bài 1 trang 71 Toán 10 Cánh diều

Cho tam giác ABC có AB = 3,5;AC = 7,5; $\widehat A = {135^o}$ $\widehat A = {135^o}$. Tính độ dài cạnh BC và bán kính R của đường tròn ngoại tiếp tam giác (làm tròn kết quả đến hàng phần mười).

Gợi ý đáp án

Áp dụng định lí cosin trong tam giác ABC ta có:

$B{C^2} = A{C^2} + A{B^2} - 2AC.AB.\cos A$ $B{C^2} = A{C^2} + A{B^2} - 2AC.AB.\cos A$

$\begin{array}{l} \Leftrightarrow B{C^2} = 7,{5^2} + 3,{5^2} - 2.7,5.3,5.\cos {135^o}\\ \Leftrightarrow B{C^2} \approx 105,6\\ \Leftrightarrow BC \approx 10,3\end{array}$ $\begin{array}{l} \Leftrightarrow B{C^2} = 7,{5^2} + 3,{5^2} - 2.7,5.3,5.\cos {135^o}\\ \Leftrightarrow B{C^2} \approx 105,6\\ \Leftrightarrow BC \approx 10,3\end{array}$

Áp dụng định lí sin trong tam giác ABC ta có: $\frac{{BC}}{{\sin A}} = 2R$ $\frac{{BC}}{{\sin A}} = 2R$

$\Rightarrow R = \frac{{BC}}{{2.\sin A}} = \frac{{10,3}}{{2.\sin {{135}^o}}} \approx 7,3$ $\Rightarrow R = \frac{{BC}}{{2.\sin A}} = \frac{{10,3}}{{2.\sin {{135}^o}}} \approx 7,3$

Bài 2 trang 71 Toán 10 Cánh diều

Cho tam giác ABC có $\widehat B = {75^o},\widehat C = {45^o} và BC = 50$ $\widehat B = {75^o},\widehat C = {45^o} và BC = 50$. Tính độ dài cạnh AB.

Gợi ý đáp án

Ta có: $\widehat B = {75^o},\widehat C = {45^o} \Rightarrow \widehat A = {180^o} - \left( {{{75}^o} + {{45}^o}} \right) = {60^o}$ $\widehat B = {75^o},\widehat C = {45^o} \Rightarrow \widehat A = {180^o} - \left( {{{75}^o} + {{45}^o}} \right) = {60^o}$

Áp dụng định lí sin trong tam giác ABC ta có:

$\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}}$ $\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}}$

$\Rightarrow AB = \sin C.\frac{{BC}}{{\sin A}} = \sin {45^o}.\frac{{50}}{{\sin {{60}^o}}} \approx 40,8$ $\Rightarrow AB = \sin C.\frac{{BC}}{{\sin A}} = \sin {45^o}.\frac{{50}}{{\sin {{60}^o}}} \approx 40,8$

Vậy độ dài cạnh AB là 40,8.

Bài 3 trang 71 Toán 10 Cánh diều

Cho tam giác ABC có AB = 6,AC = 7,BC = 8. Tính $\cos A,\sin A$ $\cos A,\sin A$ và bán kính R của đường trong ngoại tiếp tam giác ABC.

Gợi ý đáp án

Áp dụng định lí cosin trong tam giác ABC ta có:

$B{C^2} = A{C^2} + A{B^2} - 2.AC.AB.\cos A$ $B{C^2} = A{C^2} + A{B^2} - 2.AC.AB.\cos A$

$\Rightarrow \cos A = \frac{{A{C^2} + A{B^2} - B{C^2}}}{{2.AB.AC}} = \frac{{{7^2} + {6^2} - {8^2}}}{{2.7.6}} = \frac{1}{4}$ $\Rightarrow \cos A = \frac{{A{C^2} + A{B^2} - B{C^2}}}{{2.AB.AC}} = \frac{{{7^2} + {6^2} - {8^2}}}{{2.7.6}} = \frac{1}{4}$

Lại có: ${\sin ^2}A + {\cos ^2}A = 1 \Rightarrow \sin A = \sqrt {1 - {{\cos }^2}A} (do {0^o} < A \le {90^o})$ ${\sin ^2}A + {\cos ^2}A = 1 \Rightarrow \sin A = \sqrt {1 - {{\cos }^2}A} (do {0^o} < A \le {90^o})$

$\Rightarrow \sin A = \sqrt {1 - {{\left( {\frac{1}{4}} \right)}^2}} = \frac{{\sqrt {15} }}{4}$ $\Rightarrow \sin A = \sqrt {1 - {{\left( {\frac{1}{4}} \right)}^2}} = \frac{{\sqrt {15} }}{4}$

Áp dụng định lí sin trong tam giác ABC ta có: $\frac{{BC}}{{\sin A}} = 2R$ $\frac{{BC}}{{\sin A}} = 2R$

$\Rightarrow R = \frac{{BC}}{{2.\sin A}} = \frac{8}{{2.\frac{{\sqrt {15} }}{4}}} = \frac{{16\sqrt {15} }}{{15}}.$ $\Rightarrow R = \frac{{BC}}{{2.\sin A}} = \frac{8}{{2.\frac{{\sqrt {15} }}{4}}} = \frac{{16\sqrt {15} }}{{15}}.$

Vậy $\cos A = \frac{1}{4};\sin A = \frac{{\sqrt {15} }}{4};R = \frac{{16\sqrt {15} }}{{15}}.$ $\cos A = \frac{1}{4};\sin A = \frac{{\sqrt {15} }}{4};R = \frac{{16\sqrt {15} }}{{15}}.$

Bài 4 trang 71 Toán 10 Cánh diều

Tính giá trị đúng của các biểu thức sau (không dùng máy tính cầm tay):

$a) A = \cos {0^o} + \cos {40^o} + \cos {120^o} + \cos {140^o}$ $a) A = \cos {0^o} + \cos {40^o} + \cos {120^o} + \cos {140^o}$

$b) B = \sin {5^o} + \sin {150^o} - \sin {175^o} + \sin {180^o}$ $b) B = \sin {5^o} + \sin {150^o} - \sin {175^o} + \sin {180^o}$

$c) C = \cos {15^o} + \cos {35^o} - \sin {75^o} - \sin {55^o}$ $c) C = \cos {15^o} + \cos {35^o} - \sin {75^o} - \sin {55^o}$

$d) D = \tan {25^o}.\tan {45^o}.\tan {115^o}$ $d) D = \tan {25^o}.\tan {45^o}.\tan {115^o}$

$e) E = \cot {10^o}.\cot {30^o}.\cot {100^o}$ $e) E = \cot {10^o}.\cot {30^o}.\cot {100^o}$

Gợi ý đáp án

$a) A = \cos {0^o} + \cos {40^o} + \cos {120^o} + \cos {140^o}$ $a) A = \cos {0^o} + \cos {40^o} + \cos {120^o} + \cos {140^o}$

Tra bảng giá trị lượng giác của một số góc đặc biệt, ta có:

$\cos {0^o} = 1;\;\cos {120^o} = - \frac{1}{2}$ $\cos {0^o} = 1;\;\cos {120^o} = - \frac{1}{2}$

Lại có: $\cos {140^o} = - \cos \left( {{{180}^o} - {{40}^o}} \right) = - \cos {40^o}$ $\cos {140^o} = - \cos \left( {{{180}^o} - {{40}^o}} \right) = - \cos {40^o}$

$\begin{array}{l} \Rightarrow A = 1 + \cos {40^o} + \left( { - \frac{1}{2}} \right) - \cos {40^o}\\ \Leftrightarrow A = \frac{1}{2}.\end{array}$ $\begin{array}{l} \Rightarrow A = 1 + \cos {40^o} + \left( { - \frac{1}{2}} \right) - \cos {40^o}\\ \Leftrightarrow A = \frac{1}{2}.\end{array}$

b) $B = \sin {5^o} + \sin {150^o} - \sin {175^o} + \sin {180^o}$ $B = \sin {5^o} + \sin {150^o} - \sin {175^o} + \sin {180^o}$

Tra bảng giá trị lượng giác của một số góc đặc biệt, ta có:

$\sin {150^o} = \frac{1}{2};\;\sin {180^o} = 0$ $\sin {150^o} = \frac{1}{2};\;\sin {180^o} = 0$

Lại có: $\sin {175^o} = \sin \left( {{{180}^o} - {{175}^o}} \right) = \sin {5^o}$ $\sin {175^o} = \sin \left( {{{180}^o} - {{175}^o}} \right) = \sin {5^o}$

$\begin{array}{l} \Rightarrow B = \sin {5^o} + \frac{1}{2} - \sin {5^o} + 0\\ \Leftrightarrow B = \frac{1}{2}.\end{array}$ $\begin{array}{l} \Rightarrow B = \sin {5^o} + \frac{1}{2} - \sin {5^o} + 0\\ \Leftrightarrow B = \frac{1}{2}.\end{array}$

$c) C = \cos {15^o} + \cos {35^o} - \sin {75^o} - \sin {55^o}$ $c) C = \cos {15^o} + \cos {35^o} - \sin {75^o} - \sin {55^o}$

Ta có: \ $\sin {75^o} = \sin \left( {{{90}^o} - {{75}^o}} \right) = \cos {15^o}; \sin {55^o} = \sin \left( {{{90}^o} - {{55}^o}} \right) = \cos {35^o}$ $\sin {75^o} = \sin \left( {{{90}^o} - {{75}^o}} \right) = \cos {15^o}; \sin {55^o} = \sin \left( {{{90}^o} - {{55}^o}} \right) = \cos {35^o}$

$\begin{array}{l} \Rightarrow C = \cos {15^o} + \cos {35^o} - \cos {15^o} - \cos {35^o}\\ \Leftrightarrow C = 0.\end{array}$ $\begin{array}{l} \Rightarrow C = \cos {15^o} + \cos {35^o} - \cos {15^o} - \cos {35^o}\\ \Leftrightarrow C = 0.\end{array}$

$d) D = \tan {25^o}.\tan {45^o}.\tan {115^o}$ $d) D = \tan {25^o}.\tan {45^o}.\tan {115^o}$

Ta có: $\tan {115^o} = - \tan \left( {{{180}^o} - {{115}^o}} \right) = - \tan {65^o}$ $\tan {115^o} = - \tan \left( {{{180}^o} - {{115}^o}} \right) = - \tan {65^o}$

Mà: $\tan {65^o} = \cot \left( {{{90}^o} - {{65}^o}} \right) = \cot {25^o}$ $\tan {65^o} = \cot \left( {{{90}^o} - {{65}^o}} \right) = \cot {25^o}$

$\begin{array}{l} \Rightarrow D = \tan {25^o}.\tan {45^o}.\cot {25^o}\\ \Leftrightarrow D = \tan {45^o} = 1\end{array}$ $\begin{array}{l} \Rightarrow D = \tan {25^o}.\tan {45^o}.\cot {25^o}\\ \Leftrightarrow D = \tan {45^o} = 1\end{array}$

$e) E = \cot {10^o}.\cot {30^o}.\cot {100^o}$ $e) E = \cot {10^o}.\cot {30^o}.\cot {100^o}$

Ta có: $\cot {100^o} = - \cot \left( {{{180}^o} - {{100}^o}} \right) = - \cot {80^o}$ $\cot {100^o} = - \cot \left( {{{180}^o} - {{100}^o}} \right) = - \cot {80^o}$

Mà: $\cot {80^o} = \tan \left( {{{90}^o} - {{80}^o}} \right) = \tan {10^o}$ $\cot {80^o} = \tan \left( {{{90}^o} - {{80}^o}} \right) = \tan {10^o}$

$\begin{array}{l} \Rightarrow E = \cot {10^o}.\cot {30^o}.\tan {10^o}\\ \Leftrightarrow E = \cot {30^o} = \sqrt 3 .\end{array}$ $\begin{array}{l} \Rightarrow E = \cot {10^o}.\cot {30^o}.\tan {10^o}\\ \Leftrightarrow E = \cot {30^o} = \sqrt 3 .\end{array}$

Bài 5 trang 71 Toán 10 Cánh diều

Cho tam giác ABC. Chứng minh:

$b) \tan \frac{{B + C}}{2} = \cot \frac{A}{2}$ $b) \tan \frac{{B + C}}{2} = \cot \frac{A}{2}$

Gợi ý đáp án

Xét tam giác ABC, ta có:

$\widehat A + \widehat B + \widehat C = {180^o} \Rightarrow \frac{{\widehat A}}{2} + \frac{{\widehat B + \widehat C}}{2} = {90^o}$ $\widehat A + \widehat B + \widehat C = {180^o} \Rightarrow \frac{{\widehat A}}{2} + \frac{{\widehat B + \widehat C}}{2} = {90^o}$

Do đó $\frac{{\widehat A}}{2} và \frac{{\widehat B + \widehat C}}{2}$ $\frac{{\widehat A}}{2} và \frac{{\widehat B + \widehat C}}{2}$ là hai góc phụ nhau.

a) Ta có: $\sin \frac{A}{2} = \cos \left( {{{90}^o} - \frac{A}{2}} \right) = \cos \frac{{B + C}}{2}$ $\sin \frac{A}{2} = \cos \left( {{{90}^o} - \frac{A}{2}} \right) = \cos \frac{{B + C}}{2}$

b) Ta có: $\tan \frac{{B + C}}{2} = \cot \left( {{{90}^o} - \frac{{B + C}}{2}} \right) = \cot \frac{A}{2}$ $\tan \frac{{B + C}}{2} = \cot \left( {{{90}^o} - \frac{{B + C}}{2}} \right) = \cot \frac{A}{2}$

Bài 6 trang 71 Toán 10 Cánh diều

Để đo khoảng cách từ vị trí A đến vị trí B ở hai bên bờ một cái ao, bạn An đi dọc bờ ao từ vị trí A đến vị trí C và tiến hành đo các góc BAC, BCA. Biết AC = 25 m, $\widehat {BAC} = 59,{95^o};\;\widehat {BCA} = 82,{15^o}.$ $\widehat {BAC} = 59,{95^o};\;\widehat {BCA} = 82,{15^o}.$Hỏi khoảng cách từ vị trí A đến vị trí B là bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?

Gợi ý đáp án

Xét tam giác ABC, ta có: $\widehat {BAC} = 59,{95^o};\;\widehat {BCA} = 82,{15^o}.$ $\widehat {BAC} = 59,{95^o};\;\widehat {BCA} = 82,{15^o}.$

$\Rightarrow \widehat {ABC} = {180^o} - \left( {59,95 + 82,{{15}^o}} \right) = 37,{9^o}$ $\Rightarrow \widehat {ABC} = {180^o} - \left( {59,95 + 82,{{15}^o}} \right) = 37,{9^o}$

Áp dụng định lí sin trong tam giác BAC ta có: $\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}$ $\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}$

$\Rightarrow AB = \sin C.\frac{{AC}}{{\sin B}} = \sin 82,{15^o}.\frac{{25}}{{\sin 59,{{95}^o}}} \approx 28,6$ $\Rightarrow AB = \sin C.\frac{{AC}}{{\sin B}} = \sin 82,{15^o}.\frac{{25}}{{\sin 59,{{95}^o}}} \approx 28,6$

Vậy khoảng cách từ vị trí A đến vị trí B là 28,6 m.

Bài 7 trang 71 Toán 10 Cánh diều

Hai tàu đánh cá cùng xuất phát từ bến A và đi thẳng đều về hai vùng biển khác nhau, theo hai hướng tạo với nhau góc ${75^o}$ ${75^o}$. Tàu thứ nhất chạy với tốc độ 8 hải lí một giờ và tàu thứ hai chạy với tốc độ 12 hải lí một giờ. Sau 2,5 giờ thì khoảng cách giữa hai tàu là bao nhiêu hải lí (làm tròn kết quả đến hàng phần mười)?

Gợi ý đáp án

Gọi B, C lần lượt là vị trí của tàu thứ nhất và tàu thứ hai sau 2,5 giờ.

Sau 2,5 giờ:

Quãng đường tàu thứ nhất đi được là: AB = 8.2,5 = 20 (hải lí)

Quãng đường tàu thứ hai đi được là: AC = 12.2,5 = 30 (hải lí)

Áp dụng định lí cosin trong tam giác ABC ta có:

$B{C^2} = A{C^2} + A{B^2} - 2.AC.AB.\cos A$ $B{C^2} = A{C^2} + A{B^2} - 2.AC.AB.\cos A$

$\begin{array}{l} \Rightarrow B{C^2} = {30^2} + {20^2} - 2.30.20.\cos {75^o}\\ \Rightarrow B{C^2} \approx 989,4\\ \Rightarrow BC \approx 31,5\end{array}$ $\begin{array}{l} \Rightarrow B{C^2} = {30^2} + {20^2} - 2.30.20.\cos {75^o}\\ \Rightarrow B{C^2} \approx 989,4\\ \Rightarrow BC \approx 31,5\end{array}$

Vậy hai tàu cách nhau 31,5 hải lí.

Bài 8 trang 71 Toán 10 Cánh diều

Bạn A đứng ở đỉnh của tòa nhà và quan sát chiếc diều, nhận thấy góc nâng (góc nghiêng giữa phương từ mắt của bạn A tới chiếc diều và phương nằm ngang) là $\alpha = {35^o}$ $\alpha = {35^o}$; khoảng cách từ đỉnh tòa nhà tới mắt bạn A là 1,5 m. Cùng lúc đó ở dưới chân tòa nhà, bạn B cũng quan sát chiếc diều và thấy góc nâng là $\beta = {75^o}$ $\beta = {75^o}$; khoảng cách từ mặt đất đến mắt bạn B cũng là 1,5 m. Biết chiều cao của tòa nhà là h = 20 m (Hình 17). Chiếc diều bay cao bao nhiêu mét so mặt đất (làm tròn kết quả đến hàng đơn vị)?

Gợi ý đáp án

Gọi các điểm:

O là vị trí của chiếc diều.

H là hình chiếu vuông góc của chiếc diều trên mặt đất.

C, D lần lượt là hình chiếu vuông góc của A, B trên OH.

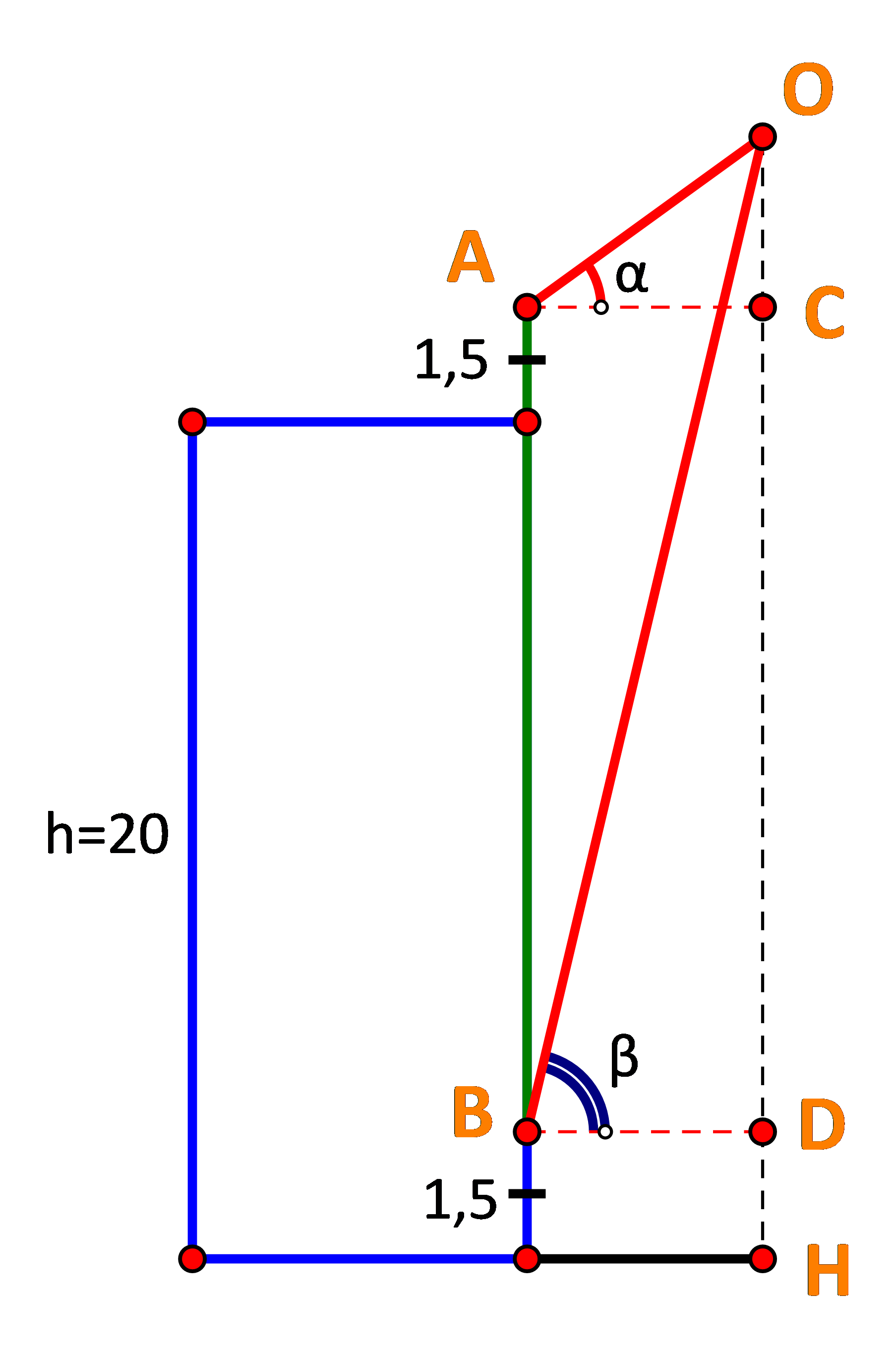
Đặt OC = x, suy ra OH = x + 20 + 1,5 =x + 21,5.

Xét tam giác OAC, ta có: $\tan \alpha = \frac{{OC}}{{AC}} \Rightarrow AC = \frac{{OC}}{{\tan \alpha }} = \frac{x}{{\tan {{35}^o}}}$ $\tan \alpha = \frac{{OC}}{{AC}} \Rightarrow AC = \frac{{OC}}{{\tan \alpha }} = \frac{x}{{\tan {{35}^o}}}$

Xét tam giác OBD, ta có: $\tan \beta = \frac{{OD}}{{BD}} \Rightarrow BD = \frac{{OD}}{{\tan \beta }} = \frac{{x + 20}}{{\tan {{75}^o}}}$ $\tan \beta = \frac{{OD}}{{BD}} \Rightarrow BD = \frac{{OD}}{{\tan \beta }} = \frac{{x + 20}}{{\tan {{75}^o}}}$

Mà: $AC = BD \Rightarrow \frac{x}{{\tan {{35}^o}}} = \frac{{x + 20}}{{\tan {{75}^o}}}$ $AC = BD \Rightarrow \frac{x}{{\tan {{35}^o}}} = \frac{{x + 20}}{{\tan {{75}^o}}}$

$\begin{array}{l} \Leftrightarrow x.\tan {75^o} = \left( {x + 20} \right).\tan {35^o}\\ \Leftrightarrow x = \frac{{20.\tan {{35}^o}}}{{\tan {{75}^o} - \tan {{35}^o}}} \approx 4,6\end{array}$ $\begin{array}{l} \Leftrightarrow x.\tan {75^o} = \left( {x + 20} \right).\tan {35^o}\\ \Leftrightarrow x = \frac{{20.\tan {{35}^o}}}{{\tan {{75}^o} - \tan {{35}^o}}} \approx 4,6\end{array}$

Suy ra OH = 26,1.

Vậy chiếc diều bay cao 26,1 m so với mặt đất.

Chia sẻ bởi: