Toán 10 Bài 2: Giải tam giác. Tính diện tích tam giác Giải SGK Toán 10 trang 77- Tập 1 sách Cánh diều
Toán 10 Cánh diều trang 77 giúp các em học sinh có thêm nhiều gợi ý tham khảo để giải các câu hỏi phần khởi động, thực hành và 7 bài tập được nhanh chóng và dễ dàng hơn.
Giải Toán 10 Cánh diều trang 77 tập 1 hướng dẫn giải bài tập trong sách giáo khoa rất chi tiết. Hy vọng rằng tài liệu sẽ giúp các em học sinh học tốt môn Toán 10. Đồng thời các thầy cô giáo, bậc phụ huynh có thể sử dụng tài liệu để hướng dẫn các em khi tự học ở nhà được thuận tiện hơn. Vậy sau đây là trọn bộ tài liệu giải Toán 10 Cánh diều trang 77 mời các bạn cùng theo dõi.
Toán 10 Bài 2: Giải tam giác. Tính diện tích tam giác
Phần Khởi động
Từ xa xưa, con người đã cần đo đạc các khoảng cách mà không thể trực tiếp đo được. Chẳng hạn, để đo khoảng cách từ vị trí A trên bờ biển tới một hòn đảo (hay con tàu,...) trên biển, người xưa đã tìm ra một cách đo khoảng cách đó như sau:
Từ vị trí A, đo góc nghiêng ![]() \(\alpha\) so với bờ biển tới một vị trí C quan sát được trên đảo. Sau đó di chuyển dọc bờ biển đến vị trí B cách A một khoảng d và tiếp tục đo góc nghiêng
\(\alpha\) so với bờ biển tới một vị trí C quan sát được trên đảo. Sau đó di chuyển dọc bờ biển đến vị trí B cách A một khoảng d và tiếp tục đo góc nghiêng ![]() \(\beta\) so với bờ biển tới vị trí C đã chọn (Hình 18).
\(\beta\) so với bờ biển tới vị trí C đã chọn (Hình 18).
Bằng cách giải tam giác ABC,họ tính được khoảng cách AC.
Giải tam giác được hiểu như thế nào?
Gợi ý đáp án
Giải tam giác là việc đi tìm một số yếu tố của tam giác khi đã biết các yếu tố khác của tam giác đó.
Trong trường hợp này, giải tam giác ABC được hiểu là tìm cạnh AC khi biết cạnh AB, góc A và góc B.
Áp dụng định lí sin ta có:
![]() \(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\)
\(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\)
Mà AB=d, ![]() \(\hat {B} =\beta; \hat {C} =180^o-\alpha -\beta\)
\(\hat {B} =\beta; \hat {C} =180^o-\alpha -\beta\)
![]() \(\Rightarrow AC = \sin \beta \frac{d}{{\sin \left( {{{180}^o} - \alpha - \beta } \right)}}\)
\(\Rightarrow AC = \sin \beta \frac{d}{{\sin \left( {{{180}^o} - \alpha - \beta } \right)}}\)
Phần Luyện tập vận dụng
Luyện tập 1 trang 74 Toán 10
Cho tam giác ABC có ![]() \(AB = 12; \widehat B = {60^o}; \widehat C = {45^o}\) . Tính diện tích của tam giác ABC.
\(AB = 12; \widehat B = {60^o}; \widehat C = {45^o}\) . Tính diện tích của tam giác ABC.
Gợi ý đáp án
Áp dụng định lí sin trong tam giác ABC, ta có:
![]() \(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\)
\(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\)
![]() \(\Rightarrow AC = \sin B.\frac{{AB}}{{\sin C}} = \sin {60^o}.\frac{{12}}{{\sin {{45}^o}}} = 6\sqrt 6\)
\(\Rightarrow AC = \sin B.\frac{{AB}}{{\sin C}} = \sin {60^o}.\frac{{12}}{{\sin {{45}^o}}} = 6\sqrt 6\)
Lại có: ![]() \(\widehat A = {180^o} - ({60^o} + {45^o}) = {75^o}\)
\(\widehat A = {180^o} - ({60^o} + {45^o}) = {75^o}\)
![]() \(\Rightarrow\) Diện tích tam giác ABC là:
\(\Rightarrow\) Diện tích tam giác ABC là:
![]() \(S = \frac{1}{2}AB.AC.\sin A = \frac{1}{2}.12.6\sqrt 6 .\sin {75^o} \approx 85,2\)
\(S = \frac{1}{2}AB.AC.\sin A = \frac{1}{2}.12.6\sqrt 6 .\sin {75^o} \approx 85,2\)
Vậy diện tích tam giác ABC là 85,2.
Luyện tập 2
Từ trên nóc của một tòa nhà cao 18,5 m, bạn Nam quan sát một cái cây cách tòa nhà 30 m và dùng giác kế đo được góc lệch giữa phương quan sát gốc cây và phương nằm ngang là ![]() \({34^o}\), góc lệch giữa phương quan sát ngọn cây và phương nằm ngang là
\({34^o}\), góc lệch giữa phương quan sát ngọn cây và phương nằm ngang là ![]() \({24^o}\). Biết chiều cao của chân giác kế là 1,5 m. Chiều cao của cái cây là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
\({24^o}\). Biết chiều cao của chân giác kế là 1,5 m. Chiều cao của cái cây là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
Lời giải chi tiết
Gọi A là vị trí đứng của Nam, B là điểm cao nhất của cây, C là vị trí gốc cây.
Gọi H là hình chiếu của A trên BC. Ta có hình vẽ:
TH1: Cây cao hơn tòa nhà
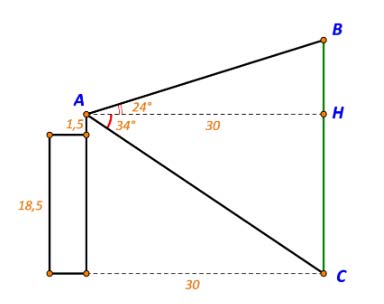
Ta có: ![]() \(\tan {24^ \circ } = \frac{{BH}}{{AH}} \Rightarrow BH = 30.\tan {24^ \circ } \approx 13,357\)
\(\tan {24^ \circ } = \frac{{BH}}{{AH}} \Rightarrow BH = 30.\tan {24^ \circ } \approx 13,357\)
![]() \(\Rightarrow BC = BH + HC \approx 13,357 + 1,5 + 18,5 = 33,357(m)\)
\(\Rightarrow BC = BH + HC \approx 13,357 + 1,5 + 18,5 = 33,357(m)\)
TH2: Cây thấp hơn tòa nhà
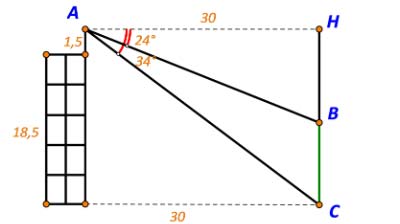
Ta có: ![]() \(\tan {24^ \circ } = \frac{{BH}}{{AH}} \Rightarrow BH = 30.\tan {24^ \circ } \approx 13,357\)
\(\tan {24^ \circ } = \frac{{BH}}{{AH}} \Rightarrow BH = 30.\tan {24^ \circ } \approx 13,357\)
![]() \(\Rightarrow BC = HC -HB \approx 1,5 + 18,5 - 13,357= 6,643(m)\)
\(\Rightarrow BC = HC -HB \approx 1,5 + 18,5 - 13,357= 6,643(m)\)
Phần Bài tập
Bài 1 trang 77 Toán 10 Cánh diều
Cho tam giác ABC có BC = 12,CA = 15,![]() \(\widehat C = {120^o}.\) Tính:
\(\widehat C = {120^o}.\) Tính:
a) Độ dài cạnh AB.
b) Số đo các góc A, B.
c) Diện tích tam giác ABC.
Gợi ý đáp án
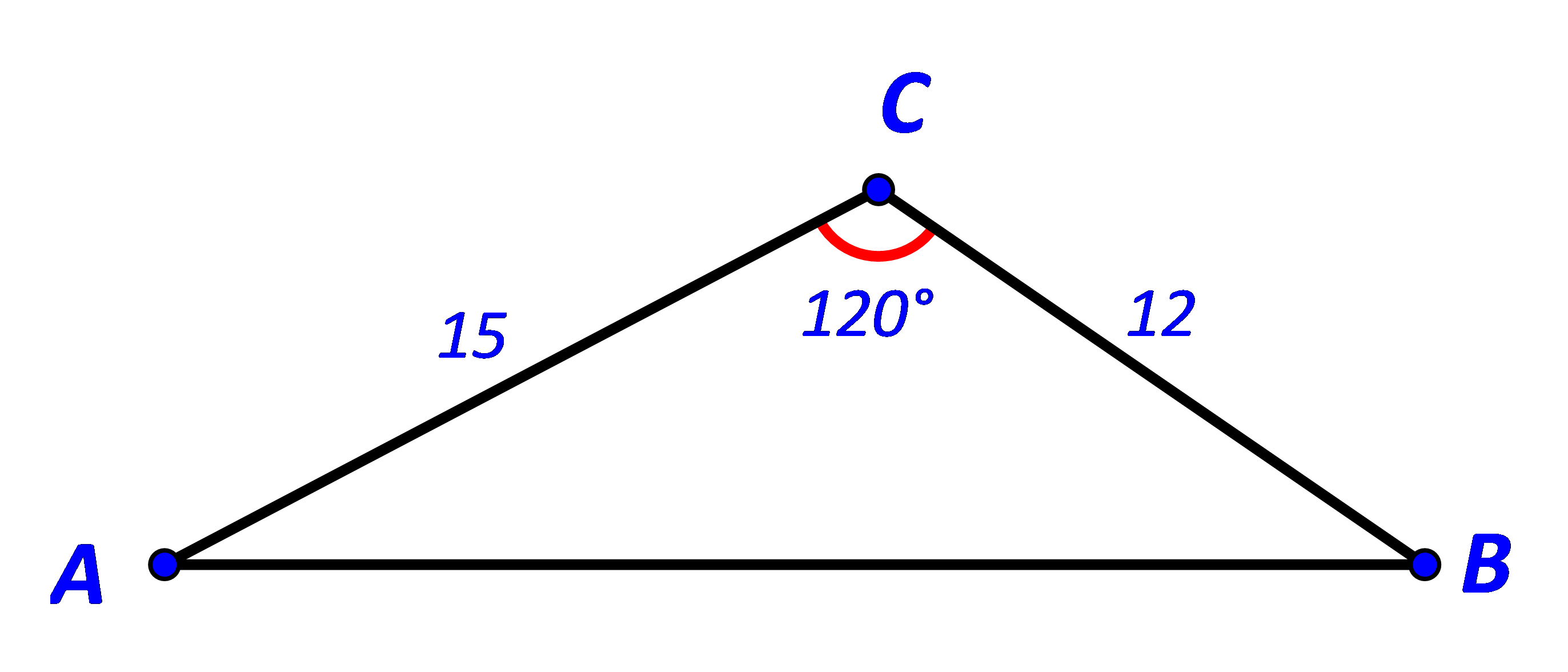
a) Áp dụng định lí cosin trong tam giác ABC ta có:
![]() \(A{B^2} = A{C^2} + B{C^2} - 2.AC.BC.\cos C\)
\(A{B^2} = A{C^2} + B{C^2} - 2.AC.BC.\cos C\)
 \(\begin{array}{l} \Leftrightarrow A{B^2} = {15^2} + {12^2} - 2.15.12.\cos {120^o}\\ \Leftrightarrow A{B^2} = 549\\ \Leftrightarrow AB \approx 23,43\end{array}\)
\(\begin{array}{l} \Leftrightarrow A{B^2} = {15^2} + {12^2} - 2.15.12.\cos {120^o}\\ \Leftrightarrow A{B^2} = 549\\ \Leftrightarrow AB \approx 23,43\end{array}\)
b) Áp dụng định lí sin trong tam giác ABC, ta có:
![]() \(\frac{{BC}}{{\sin A}} = \frac{{AB}}{{\sin C}}\)
\(\frac{{BC}}{{\sin A}} = \frac{{AB}}{{\sin C}}\)
![]() \(\Rightarrow \sin A = \frac{{BC}}{{AB}}.\sin C = \frac{{12}}{{23,43}}.\sin {120^o} \approx 0,44\)
\(\Rightarrow \sin A = \frac{{BC}}{{AB}}.\sin C = \frac{{12}}{{23,43}}.\sin {120^o} \approx 0,44\)
![]() \(\Rightarrow \widehat A \approx {26^o} hoặc \widehat A \approx {154^o} (Loại)\)
\(\Rightarrow \widehat A \approx {26^o} hoặc \widehat A \approx {154^o} (Loại)\)
Khi đó:![]() \(\widehat B = {180^o} - ({26^o} + {120^o}) = {34^o}\)
\(\widehat B = {180^o} - ({26^o} + {120^o}) = {34^o}\)
c)
Diện tích tam giác ABC là: ![]() \(S = \frac{1}{2}CA.CB.\sin C = \frac{1}{2}.15.12.\sin {120^o} = 45\sqrt 3\)
\(S = \frac{1}{2}CA.CB.\sin C = \frac{1}{2}.15.12.\sin {120^o} = 45\sqrt 3\)
Bài 2 trang 77 Toán 10 Cánh diều
Cho tam giác ABC có AB = 5,BC = 7,![]() \(\widehat A = {120^o}\). Tính độ dài cạnh AC.
\(\widehat A = {120^o}\). Tính độ dài cạnh AC.
Gợi ý đáp án
Áp dụng định lí sin trong tam giác ABC ta có:
![]() \(\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}}\)
\(\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}}\)
![]() \(\Rightarrow \sin C = \sin A.\frac{{AB}}{{BC}} = \sin {120^o}.\frac{5}{7} = \frac{{5\sqrt 3 }}{{14}}\)
\(\Rightarrow \sin C = \sin A.\frac{{AB}}{{BC}} = \sin {120^o}.\frac{5}{7} = \frac{{5\sqrt 3 }}{{14}}\)
![]() \(\Rightarrow \widehat C \approx 38,{2^o} hoặc \widehat C \approx 141,{8^o} (Loại)\)
\(\Rightarrow \widehat C \approx 38,{2^o} hoặc \widehat C \approx 141,{8^o} (Loại)\)
Ta có: ![]() \(\widehat A = {120^o},\widehat C = 38,{2^o} \Rightarrow \widehat B = {180^o} - \left( {{{120}^o} + 38,{2^o}} \right) = 21,{8^o}\)
\(\widehat A = {120^o},\widehat C = 38,{2^o} \Rightarrow \widehat B = {180^o} - \left( {{{120}^o} + 38,{2^o}} \right) = 21,{8^o}\)
Áp dụng định lí cosin trong tam giác ABC ta có:
 \(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\\ \Leftrightarrow A{C^2} = {5^2} + {7^2} - 2.5.7.\cos 21,{8^o}\\ \Rightarrow A{C^2} \approx 9\\ \Rightarrow AC = 3\end{array}\)
\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\\ \Leftrightarrow A{C^2} = {5^2} + {7^2} - 2.5.7.\cos 21,{8^o}\\ \Rightarrow A{C^2} \approx 9\\ \Rightarrow AC = 3\end{array}\)
Vậy độ dài cạnh AC là 3.
Bài 3 trang 77 Toán 10 Cánh diều
Cho tam giác ABC có ![]() \(AB = 100,\widehat B = {100^o},\widehat C = {45^o}.\) Tính:
\(AB = 100,\widehat B = {100^o},\widehat C = {45^o}.\) Tính:
a) Độ dài các cạnh AC, BC
b) Diện tích tam giác ABC.
Gợi ý đáp án
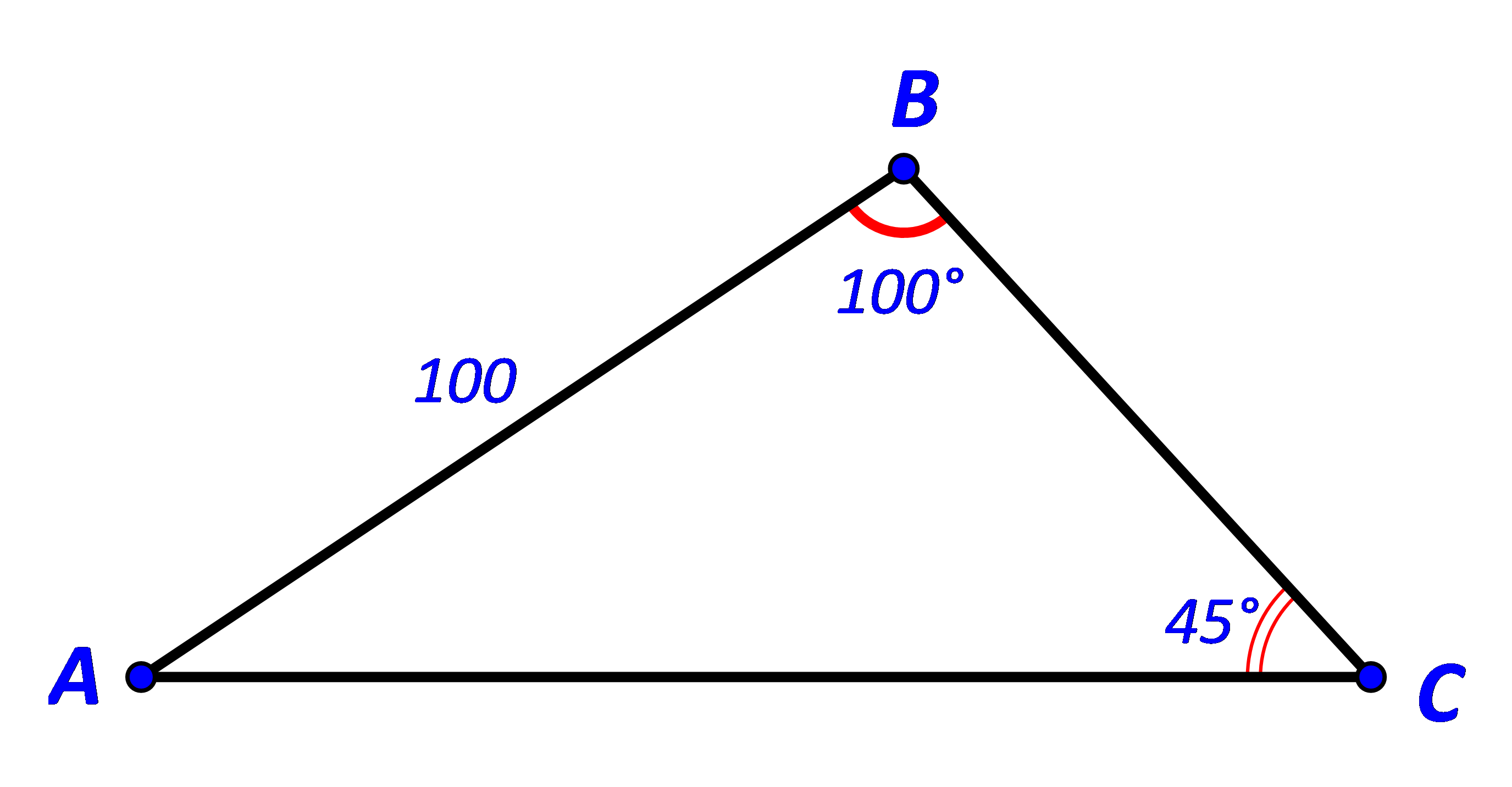
a)
Ta có: ![]() \(\widehat A = {180^o} - (\widehat B + \widehat C) \Rightarrow \widehat A = {180^o} - ({100^o} + {45^o}) = {35^o}\)
\(\widehat A = {180^o} - (\widehat B + \widehat C) \Rightarrow \widehat A = {180^o} - ({100^o} + {45^o}) = {35^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
![]() \(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}} = \frac{{BC}}{{\sin A}}\)
\(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}} = \frac{{BC}}{{\sin A}}\)
 \(\Rightarrow \left\{ \begin{array}{l}AC = \sin B.\frac{{AB}}{{\sin C}}\\BC = \sin A.\frac{{AB}}{{\sin C}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}AC = \sin {100^o}.\frac{{100}}{{\sin {{45}^o}}} \approx 139,3\\BC = \sin {35^o}.\frac{{100}}{{\sin {{45}^o}}} \approx 81,1\end{array} \right.\)
\(\Rightarrow \left\{ \begin{array}{l}AC = \sin B.\frac{{AB}}{{\sin C}}\\BC = \sin A.\frac{{AB}}{{\sin C}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}AC = \sin {100^o}.\frac{{100}}{{\sin {{45}^o}}} \approx 139,3\\BC = \sin {35^o}.\frac{{100}}{{\sin {{45}^o}}} \approx 81,1\end{array} \right.\)
b)
Diện tích tam giác ABC là: ![]() \(S = \frac{1}{2}.BC.AC.\sin C = \frac{1}{2}.81,1.139,3.\sin {45^o} \approx 3994,2.\)
\(S = \frac{1}{2}.BC.AC.\sin C = \frac{1}{2}.81,1.139,3.\sin {45^o} \approx 3994,2.\)
Bài 4 trang 77 Toán 10 Cánh diều
Cho tam giác ABC có AB = 12,AC = 15,BC = 20. Tính:
a) Số đo các góc A, B, C.
b) Diện tích tam giác ABC.
Gợi ý đáp án
a) Áp dụng định lí cosin trong tam giác ABC, ta có:
![]() \(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\;\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\)
\(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\;\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\)
Thay a = BC = 20;b = AC = 15;c = AB = 12.
![]() \(\Rightarrow \cos A = - \frac{{31}}{{360}};\;\cos B = \frac{{319}}{{480}}\)
\(\Rightarrow \cos A = - \frac{{31}}{{360}};\;\cos B = \frac{{319}}{{480}}\)
![]() \(\Rightarrow \widehat A = 94,{9^o};\;\widehat B = 48,{3^o}\)
\(\Rightarrow \widehat A = 94,{9^o};\;\widehat B = 48,{3^o}\)
![]() \(\Rightarrow \widehat C = {180^o} - \left( {94,{9^o} + 48,{3^o}} \right) = 36,{8^o}\)
\(\Rightarrow \widehat C = {180^o} - \left( {94,{9^o} + 48,{3^o}} \right) = 36,{8^o}\)
b)
Diện tích tam giác ABC là: ![]() \(S = \frac{1}{2}.bc.\sin A = \frac{1}{2}.15.12.\sin 94,{9^o} \approx 89,7.\)
\(S = \frac{1}{2}.bc.\sin A = \frac{1}{2}.15.12.\sin 94,{9^o} \approx 89,7.\)
Bài 5 trang 77 Toán 10 Cánh diều
Tính độ dài cạnh AB trong mỗi trường hợp sau:
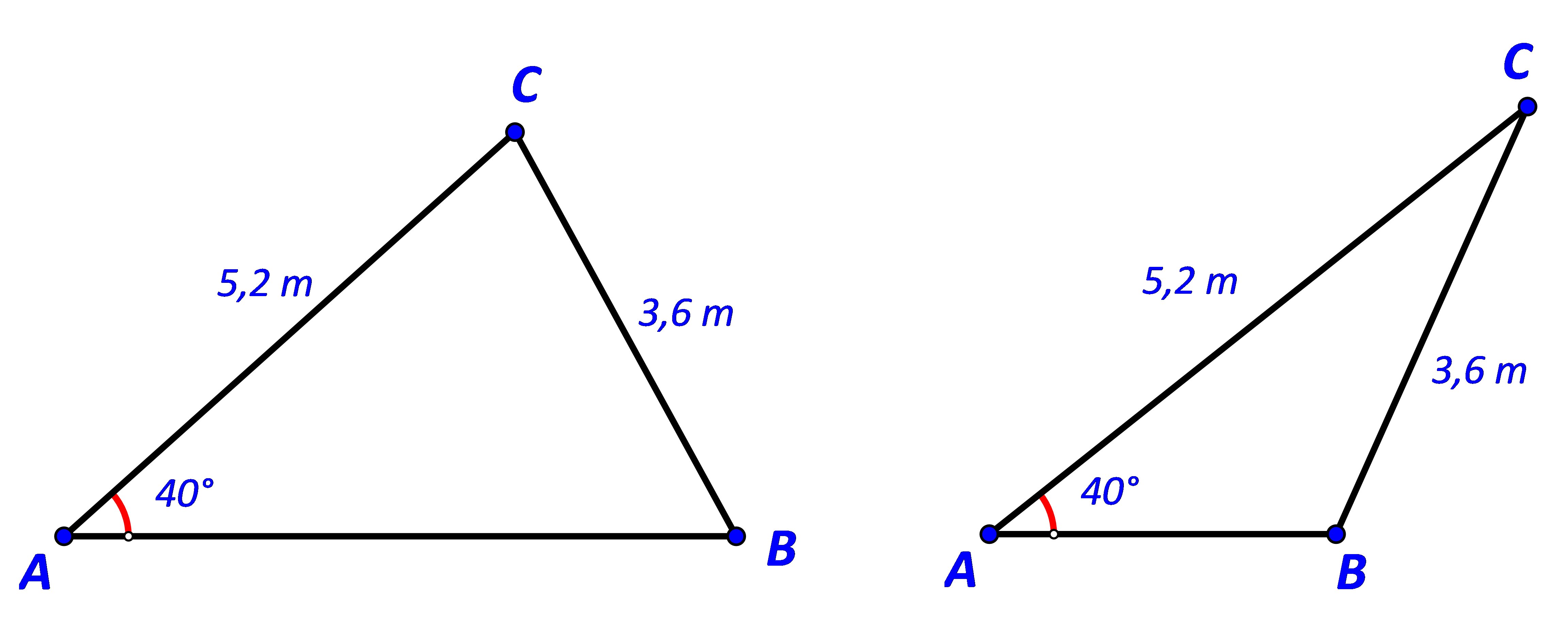
Gợi ý đáp án
Áp dụng định lí sin trong tam giác ABC, ta có:
![]() \(\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}}\)
\(\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}}\)
![]() \(\Rightarrow \sin B = \frac{{AC.\sin A}}{{BC}} = \frac{{5,2.\sin {{40}^o}}}{{3,6}} \approx 0,93\)
\(\Rightarrow \sin B = \frac{{AC.\sin A}}{{BC}} = \frac{{5,2.\sin {{40}^o}}}{{3,6}} \approx 0,93\)
![]() \(\Rightarrow \widehat B \approx 68,{2^o} hoặc \widehat B \approx 111,{8^o}\)
\(\Rightarrow \widehat B \approx 68,{2^o} hoặc \widehat B \approx 111,{8^o}\)
Trường hợp 1![]() \(: \widehat B \approx 68,{2^o}\)
\(: \widehat B \approx 68,{2^o}\)
Ta có:![]() \(\widehat C = {180^o} - (\widehat A + \widehat B) = {180^o} - ({40^o} + 68,{2^o}) = 71,{8^o}\)
\(\widehat C = {180^o} - (\widehat A + \widehat B) = {180^o} - ({40^o} + 68,{2^o}) = 71,{8^o}\)
Áp dụng định lí sin trong tam giác ABC, ta có:
![]() \(\frac{{BC}}{{\sin A}} = \frac{{AB}}{{\sin C}}\)
\(\frac{{BC}}{{\sin A}} = \frac{{AB}}{{\sin C}}\)
![]() \(\Rightarrow AB = \sin C.\frac{{BC}}{{\sin A}} = \sin 71,{8^o}.\frac{{3,6}}{{\sin {{40}^o}}} \approx 5,32\)
\(\Rightarrow AB = \sin C.\frac{{BC}}{{\sin A}} = \sin 71,{8^o}.\frac{{3,6}}{{\sin {{40}^o}}} \approx 5,32\)
Trường hợp 2: ![]() \(\widehat B \approx 111,{8^o}\)
\(\widehat B \approx 111,{8^o}\)
Ta có: ![]() \(\widehat C = {180^o} - (\widehat A + \widehat B) = {180^o} - ({40^o} + 111,{8^o}) = 28,{2^o}\)
\(\widehat C = {180^o} - (\widehat A + \widehat B) = {180^o} - ({40^o} + 111,{8^o}) = 28,{2^o}\)
Áp dụng định lí sin trong tam giác ABC, ta có:
![]() \(\frac{{BC}}{{\sin A}} = \frac{{AB}}{{\sin C}}\)
\(\frac{{BC}}{{\sin A}} = \frac{{AB}}{{\sin C}}\)
![]() \(\Rightarrow AB = \sin C.\frac{{BC}}{{\sin A}} = \sin 28,{2^o}.\frac{{3,6}}{{\sin {{40}^o}}} \approx 2,65\)
\(\Rightarrow AB = \sin C.\frac{{BC}}{{\sin A}} = \sin 28,{2^o}.\frac{{3,6}}{{\sin {{40}^o}}} \approx 2,65\)
Vậy AB = 5,32 hoặc AB = 2,65.
Bài 6 trang 77 Toán 10 Cánh diều
Để tính khoảng cách giữa hai địa điểm A và B mà ta không thể đi trực tiếp từ A đến B (hai địa điểm nằm ở hai bên bờ một hồ nước, một đầm lầy, …), người ta tiến hành như sau: Chọn một địa điểm C sao cho ta đo được các khoảng cách AC, CB và góc ACB. Sau khi đo, ta nhận được: AC = 1 km, CB = 800 m và ![]() \(\widehat {ACB} = {105^o}\) (Hình 31). Tính khoảng cách AB (làm tròn kết quả đến hàng phần mười đơn vị mét).
\(\widehat {ACB} = {105^o}\) (Hình 31). Tính khoảng cách AB (làm tròn kết quả đến hàng phần mười đơn vị mét).
Gợi ý đáp án
Đổi: 1 km = 1000 m. Do đó AC = 1000 m.
Áp dụng định lí cosin trong tam giác ABC ta có:
![]() \(A{B^2} = A{C^2} + B{C^2} - 2.AC.BC.\cos C\)
\(A{B^2} = A{C^2} + B{C^2} - 2.AC.BC.\cos C\)
 \(\begin{array}{l} \Rightarrow A{B^2} = {1000^2} + {800^2} - 2.1000.800.\cos {105^o}\\ \Rightarrow A{B^2} \approx 2054110,5\\ \Rightarrow AB \approx 1433,2\end{array}\)
\(\begin{array}{l} \Rightarrow A{B^2} = {1000^2} + {800^2} - 2.1000.800.\cos {105^o}\\ \Rightarrow A{B^2} \approx 2054110,5\\ \Rightarrow AB \approx 1433,2\end{array}\)
Vậy khoảng cách AB là 1433,2 m.
Bài 7 trang 77 Toán 10 Cánh diều
Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ các vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là ![]() \({45^o}\) và
\({45^o}\) và ![]() \({75^o}.\) Biết khoảng cách giữa hai vị trí A, B là 30 m (Hình 32). Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
\({75^o}.\) Biết khoảng cách giữa hai vị trí A, B là 30 m (Hình 32). Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
Gợi ý đáp án
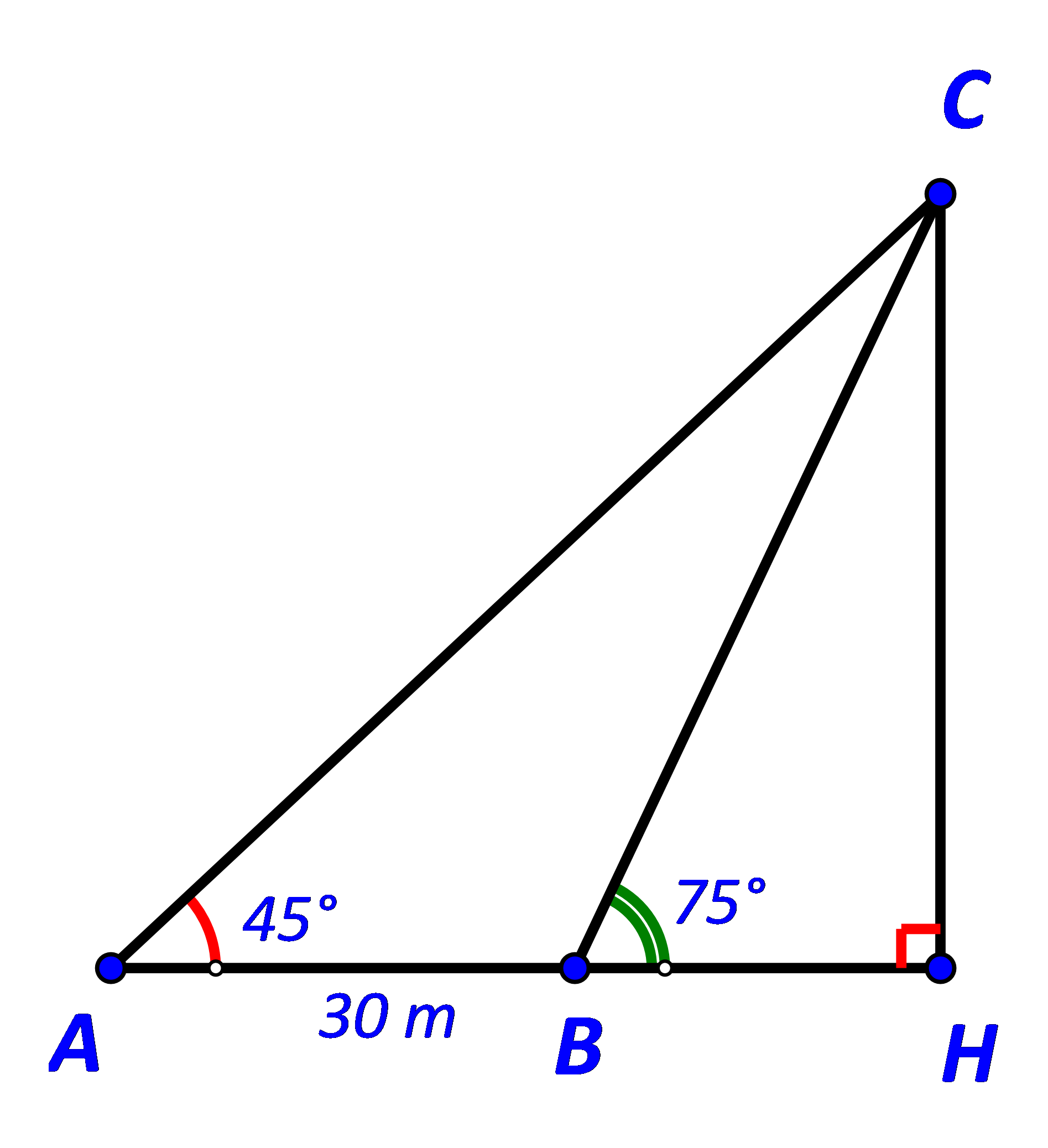
Gọi C là vị trí ngọn hải đăng và H là hình chiếu của C trên AB.
Khi đó CH là khoảng cách từ ngọn hải đăng tới bờ biển.
Ta có: ![]() \(\widehat {ACB} = \widehat {HBC} - \widehat {BAC} = {75^o} - {45^o} = {30^o}; \, \widehat {ABC} = {180^o} - {75^o} = {105^o}\)
\(\widehat {ACB} = \widehat {HBC} - \widehat {BAC} = {75^o} - {45^o} = {30^o}; \, \widehat {ABC} = {180^o} - {75^o} = {105^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
![]() \(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}\)
\(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}\)
![]() \(\Rightarrow AC = \sin B.\frac{{AB}}{{\sin C}} = \sin {105^o}.\frac{{30}}{{\sin {{30}^o}}} \approx 58\)
\(\Rightarrow AC = \sin B.\frac{{AB}}{{\sin C}} = \sin {105^o}.\frac{{30}}{{\sin {{30}^o}}} \approx 58\)
Tam giác ACH vuông tại H nên ta có:
![]() \(CH = \sin A.AC = \sin {45^o}.58 \approx 41\)
\(CH = \sin A.AC = \sin {45^o}.58 \approx 41\)
Vậy ngọn hải đăng cách bờ biển 41 m.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
-
Tú NguyễnThích · Phản hồi · 1 · 10:25 16/09
-
 Trịnh Thị ThanhThích · Phản hồi · 0 · 14:53 16/09
Trịnh Thị ThanhThích · Phản hồi · 0 · 14:53 16/09
-












 Toán 10 Kết nối tri thức
Toán 10 Kết nối tri thức
 Toán 10 Chân trời sáng tạo
Toán 10 Chân trời sáng tạo
 Toán 10 Cánh Diều
Toán 10 Cánh Diều
 Soạn văn 10 Chân trời sáng tạo
Soạn văn 10 Chân trời sáng tạo
 Soạn văn 10 Cánh Diều
Soạn văn 10 Cánh Diều
 Soạn văn 10 Kết nối tri thức
Soạn văn 10 Kết nối tri thức
 Tiếng Anh 10 Global Success
Tiếng Anh 10 Global Success
 Tiếng anh 10 Friends Global
Tiếng anh 10 Friends Global
 Tiếng Anh 10 Explore New Worlds
Tiếng Anh 10 Explore New Worlds









