Toán 10 Bài 3: Các số liệu đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm Giải SGK Toán 10 trang 41 - Tập 2 sách Cánh diều

Giải Toán 10 Bài 3: Các số liệu đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm sách Cánh diều là tài liệu vô cùng hữu ích giúp các em học sinh lớp 10 có thêm nhiều gợi ý tham khảo, dễ dàng đối chiếu kết quả khi làm bài tập toán trang 41 tập 2.

Giải SGK Toán 10 Bài 3 trang 41 Cánh diều tập 2 được biên soạn chi tiết, bám sát nội dung trong sách giáo khoa. Mỗi bài toán đều được giải thích cụ thể, chi tiết. Qua đó giúp các em củng cố, khắc sâu thêm kiến thức đã học trong chương trình chính khóa; có thể tự học, tự kiểm tra được kết quả học tập của bản thân. Nội dung chi tiết bài Giải Toán 10 Bài 3 trang 41 tập 2 mời các bạn cùng đón đọc tại đây.

Giải Toán 10 trang 41 Cánh diều - Tập 2

Bài 1 trang 41

Trong 5 lần nhảy xa, hai bạn Hùng và Trung có kết quả (đơn vị: mét) lần lượt là

a. Kết quả trung bình của hai bạn có bằng nhau hay không?

b. Tính phương sai của mẫu số liệu thống kê kết quả 5 lần nhảy xa của mỗi bạn. Từ đó cho biết bạn nào có kết quả nhảy xa ổn định hơn.

Gợi ý đáp án

a.

• Kết quả trung bình của Hùng là: \(\bar{x}=2,5\)
• Kết quả trung bình của Trung là: \(\bar{x}=2,5\)

Vậy kết quả trung bình của hai bạn có bằng nhau.

b. Ta có:

\(s_H^2=\frac{(2,4-2,5)^2+(2,6-2,5)^2+(2,4-2,5)^2+(2,5-2,5)^2+(2,6-2,5)^2}{5}=0.008\)

và \(s_T^2=\frac{(2,4-2,5)^2+(2,5-2,5)^2+(2,5-2,5)^2+(2,5-2,5)^2+(2,6-2,5)^2}{5}=0.004\)

Bạn Trung có kết quả nhảy xa ổn định hơn.

Bài 2 trang 41

Biểu đồ đoạn thẳng ở Hình 3 biểu diễn tốc độ tăng trưởng GDP của Việt Nam giai đoạn 2012 – 2019.

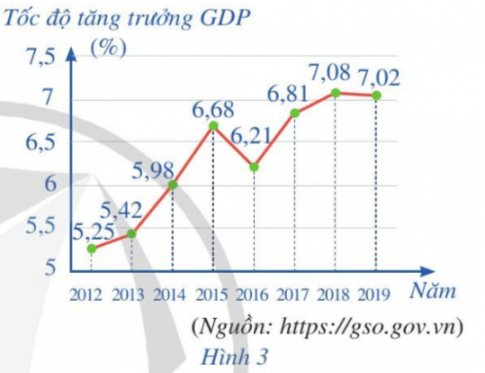
a. Viết mẫu số liệu thống kê tốc độ tăng trưởng GDP nhận được từ biểu đồ ở Hình 3.

b. Tìm khoảng biến thiên của mẫu số liệu đó.

c. Tìm khoảng tứ phân vị của mẫu số liệu đó.

d. Tính phương sai và độ lệch chuẩn của mẫu số liệu đó.

Gợi ý đáp án

a. 5, 25 5,42 5,98 6,68 6,21 6,81 7,08 7,02

b. Mẫu số liệu được sắp xếp theo thứ tự không giảm là: 5, 25 5,42 5,98 6,21 6,68 6,81 7,02 7,08

R=7,08-5,25=1,83

c. Trung vị của mẫu số liệu là: \(Q_2=\frac{6,21+6,68}{2}=6445\)

Trung vị của dãy 5, 25 5,42 5,98 6,21 là \(Q_1=\frac{5,42+5,98}{2}=5,7\)

Trung vị của dãy 6,68 6,81 7,02 7,08 là \(Q_3=\frac{6,81+7,02}{2}=6,915\)

\(\Rightarrow \Delta_Q=Q_3-Q_1=6,915-5,7=1,215\)

d. Ta có:\(\bar{x}=6,31\)

\(s^2=\frac{(5,25-6,31)^2+(5,42-6,31)^2+(5,98-6,31)^2+(6,68-6,31)^2+(6,21-6,31)^2+6,81-6,31)^2+(7,08-6,31)^2}{8}\\+\frac{(7,02-6,31)^2}{8}\)

=0.4398125

\(\Rightarrow s=\sqrt{s^2} \approx 0,66\)

Bài 3 trang 41

Biểu đồ đoạn thẳng ở Hình 4 biểu diễn giá vàng bán ra trong bảy ngày đầu tiên của tháng 6 năm 2021.

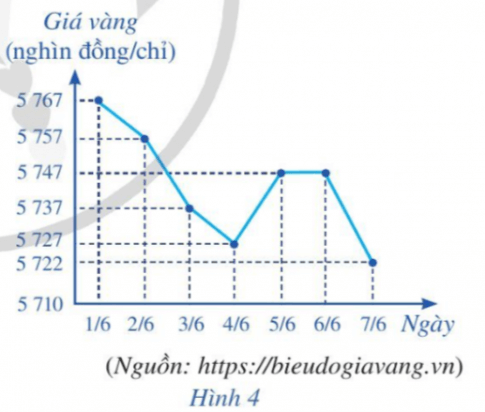
a. Viết mẫu số liệu thống kê giá vàng bán ra nhận được từ biểu đồ ở Hình 4.

b. Tìm khoảng biến thiên của mẫu số liệu đó.

c. Tìm khoảng tứ phân vị của mẫu số liệu đó.

d. Tính phương sai và độ lệch chuẩn của mẫu số liệu đó.

Gợi ý đáp án

a. 5767 5757 5737 5727 5747 5747 5722

b. Mẫu số liệu được sắp xếp theo thứ tự không giảm là: 5722 5727 5737 5747 5747 5757 5767

R=5767-5722=45

c.

• Trung vị của mẫu số liệu là: \(Q_2=5747\)
• Trung vị của dãy 5722 5727 5737 là \(Q_1=5727\)
• Trung vị của dãy 5747 5757 5767 là \(Q_3=5757\)

\(\Rightarrow \Delta_Q=Q_3-Q_1=5757-5727=30\)

d. Ta có: \(\bar{x} \approx 5743,43\)

\(s^2=\frac{(5767-5743,43)^2+(5757-5743,43)^2+...+(5747-5743,43)^2+(5722-5743,43)^2}{7} \approx 219,39\)

\(\Rightarrow s=\sqrt{s^2} \approx 14,81\)

Bài 4 trang 41

Để biết cây đậu phát triển như thế nào sau khi gieo hạt, bạn Châu gieo 5 hạt đậu vào 5 chậu riêng biệt và cung cấp cho chúng lượng nước, ánh sáng như nhau. Sau hai tuần, 5 hạt đậu đã nảy mầm và phát triển thành 5 cây con. Bạn Châu đo chiều cao từ rễ đến ngọn của mỗi cây (đơn vị: mi-li-mét) và ghi kết quả là mẫu số liệu sau:

112 102 106 94 101

a. Tính phương sai và độ lệch chuẩn của mẫu số liệu trên.

b. Theo em, các cây có phát triển đồng đều hay không?

Gợi ý đáp án

Ta có: \(\bar{x}=103\)

\(\Rightarrow s^2=\frac{(112-103)^2+(102-103)^2+(106-103)^2+(94-103)^2+(101-103)^2}{5}=35,2\)

\(\Rightarrow s \approx 5,94\)