Toán 10 Bài 1: Tọa độ của vectơ Giải SGK Toán 10 trang 44 - Tập 2 sách Chân trời sáng tạo

Tải về Bình luận

Bài trước

Mục lục

Bài sau

Giải Toán lớp 10 trang 44 tập 2 Chân trời sáng tạo giúp các em học sinh có thêm nhiều gợi ý tham khảo để giải các câu hỏi phần mở đầu và 11 bài tập trang 44, 45 được nhanh chóng và dễ dàng hơn.

Giải Toán 10 Chân trời sáng tạo tập 2 trang 44, 45 hướng dẫn giải bài tập Tọa độ của vectơ trong sách giáo khoa rất chi tiết. Hy vọng rằng tài liệu sẽ giúp các em học sinh học tốt môn Toán 10. Đồng thời các thầy cô giáo, bậc phụ huynh có thể sử dụng tài liệu để hướng dẫn các em khi tự học ở nhà được thuận tiện hơn. Vậy sau đây là trọn bộ tài liệu giải Toán 10 trang 44, 45 Chân trời sáng tạo mời các bạn cùng theo dõi.

Toán 10 Bài 1: Tọa độ của vectơ

Phần Khởi động

Tìm cách xác định vị trí các quân mã trên bàn cờ vua.

Lời giải:

Bàn cờ được chia thành 8 hàng (1-8) và 8 cột (a-h) đánh số như hình vẽ.

Do đó mỗi quân cờ xác định khi biết số hàng và số cột, tương ứng với cặp số (x;y) trong đó x là số hàng, y là số cột.

Khi đó hai mã đen có vị trí là (8;b) và (4;e)

Hai mã trắng có vị trí là (3;c) và (3;f)

Cách 2:

Đặt gốc tọa độ tại góc dưới, bên trái của bàn cờ. Coi mỗi ô vuông là 1 đơn vị.

Ta xác định được tọa độ của các con mã như sau:

Hai mã đen có tọa độ lần lượt là (2;8), (5;4)

Hai mã trắng có tọa độ lần lượt là (3;3) và (6;3)

Phần Bài tập

Bài 1 trang 44

Bài tập 1. Trên trục (O; $\vec{e})$ $\vec{e})$ cho các điểm A, B, C, D có tọa độ lần lượt là 4; -1; -5; 0.

a. Vẽ trục và biểu diễn các điểm đã cho lên trên trục đó.

b. Hai vectơ $\vec{AB}$ $\vec{AB}$ và $\vec{CD}$ $\vec{CD}$ cùng hướng hay ngược hướng.

Gợi ý đáp án

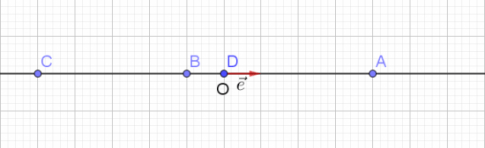
b. Hai vectơ $\vec{AB}$ $\vec{AB}$ và $\vec{CD}$ $\vec{CD}$ ngược hướng nhau.

Bài 2 trang 45

Chứng minh rằng:

a. $\vec{a}$ $\vec{a}$ = (4; -6) và $\vec{b}$ $\vec{b}$ = (-2; 3) là hai vectơ ngược hướng.

b. $\vec{a}$ $\vec{a}$= (-2; 3) và $\vec{b}$ $\vec{b}$ = (-8; 12) là hai vectơ cùng hướng.

c. $\vec{a}$ $\vec{a}$ = (0; 4) và $\vec{b}$ $\vec{b}$ = (0; -4) là hai vectơ đối nhau.

Gợi ý đáp án

a. Nhận thấy: $\vec{a} = -2\vec{b} \Rightarrow \vec{a} và \vec{b}$ $\vec{a} = -2\vec{b} \Rightarrow \vec{a} và \vec{b}$ ngược hướng.

b. Nhận thấy: $\vec{a} = 4\vec{b} \Rightarrow \vec{a} và \vec{b}$ $\vec{a} = 4\vec{b} \Rightarrow \vec{a} và \vec{b}$ cùng hướng.

c. Ta có: $|\vec{a}| = \sqrt{0^{2} + 4^{2}} = 4; |\vec{b}| = \sqrt{0^{2} + (-4)^{2}} = 4$ $|\vec{a}| = \sqrt{0^{2} + 4^{2}} = 4; |\vec{b}| = \sqrt{0^{2} + (-4)^{2}} = 4$

Nhận thấy: $\vec{a} = -\vec{b} mà |\vec{a}| = |\vec{b}| = 4$ $\vec{a} = -\vec{b} mà |\vec{a}| = |\vec{b}| = 4$

$\Rightarrow \vec{a}$ $\Rightarrow \vec{a}$ và $\vec{b}$ $\vec{b}$ là hai vectơ đối nhau.

Bài 3 trang 45

Tìm tọa độ các vectơ sau:

$a. \vec{a} = 2\vec{i} + 7\vec{j};$ $a. \vec{a} = 2\vec{i} + 7\vec{j};$

$b.\vec{b}=-\vec{i}+3\vec{j};$ $b.\vec{b}=-\vec{i}+3\vec{j};$

$c. \vec{c} = 4\vec{i};$ $c. \vec{c} = 4\vec{i};$

$d. \vec{d} = -9\vec{j}.$ $d. \vec{d} = -9\vec{j}.$

Gợi ý đáp án

$a. \vec{a} = (2; 7);$ $a. \vec{a} = (2; 7);$

$b. \vec{b} = (-1; 3);$ $b. \vec{b} = (-1; 3);$

$c. \vec{c} = (4; 0);$ $c. \vec{c} = (4; 0);$

$d. \vec{d} = (0; -9)$ $d. \vec{d} = (0; -9)$

Bài 4 trang 45

Cho bốn điểm A(3; 5), B(4; 0), C(0; -3), D(2; 2). Trong các điểm đã cho, hãy tìm điểm:

a. Thuộc trục hoành;

b. Thuộc trục tung;

c. Thuộc đường phân giác của góc phần tư thứ nhất

Gợi ý đáp án

a. Điểm B(4; 0) thuộc trục hoành.

b. Điểm C(0; -3) thuộc trục tung.

c. Điểm D(2; 2) thuộc đường phân giác của góc phần tư thứ nhất.

Bài 5 trang 45

Cho điểm $M(x_{0}; y_{0})$ $M(x_{0}; y_{0})$. Tìm tọa độ:

a. Điểm H là hình chiếu vuông góc của điểm M trên trục Ox;

b. Điểm M' đối xứng với M qua trục Ox;

c. Điểm K là hình chiếu vuông góc của điểm M trên trục Oy;

d. Điểm M'' đối xứng với M qua trục Oy.

e. Điểm C đối xứng với điểm M qua gốc tọa độ.

Gợi ý đáp án

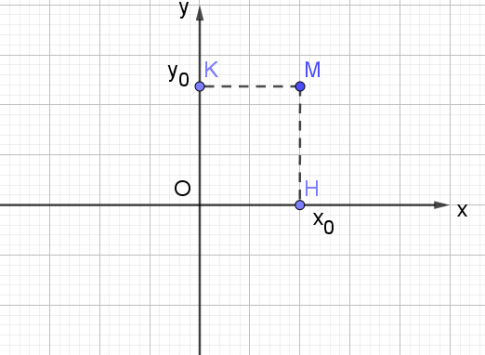
a. $H(x_{0}; 0)$ $H(x_{0}; 0)$

b. M' đối xứng với M qua trục $Ox \Rightarrow H$ $Ox \Rightarrow H$ là trung điểm của MM'

$\Rightarrow \left\{\begin{matrix}x_{M$ $\Rightarrow \left\{\begin{matrix}x_{M'} = 2x_{H} - x_{M}\\ y_{M'} = 2y_{H} - y_{M}\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x_{M'} = 2x_{0} - x_{0}\\ y_{M'} = 2.0 - y_{0}\end{matrix}\right. \left\{\begin{matrix}x_{M'} = x_{0}\\ y_{M'} = - y_{0}\end{matrix}\right.$

Vậy $M'(x_{0}; -y_{0}).$

c. $K(0; y_{0})$ $K(0; y_{0})$

d. M'' đối xứng với M qua trục Oy $\Rightarrow K$ $\Rightarrow K$ là trung điểm của MM''

$\Rightarrow \left\{\begin{matrix}x_{M$ $\Rightarrow \left\{\begin{matrix}x_{M''} = 2x_{K} - x_{M}\\ y_{M''} = 2y_{K} - y_{M}\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x_{M''} = 2.0 - x_{0}\\ y_{M''} = 2.y_{0} - y_{0}\end{matrix}\right. \left\{\begin{matrix}x_{M''} = -x_{0}\\ y_{M'} = y_{0}\end{matrix}\right.$

Vậy $M''(-x_{0}; y_{0})$.

e. C đối xứng với M qua gốc tọa độ O nên O là trung điểm của CM.

$\Rightarrow \left\{\begin{matrix}x_{C} = 2x_{O} - x_{M}\\ y_{C} = 2y_{O} - y_{M}\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x_{C} = 2.0 - x_{0}\\ y_{C} = 2.0 - y_{0}\end{matrix}\right. \left\{\begin{matrix}x_{C} = -x_{0}\\ y_{M$ $\Rightarrow \left\{\begin{matrix}x_{C} = 2x_{O} - x_{M}\\ y_{C} = 2y_{O} - y_{M}\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x_{C} = 2.0 - x_{0}\\ y_{C} = 2.0 - y_{0}\end{matrix}\right. \left\{\begin{matrix}x_{C} = -x_{0}\\ y_{M'} = -y_{0}\end{matrix}\right.$

Vậy $C(-x_{0}; -y_{0}).$ $C(-x_{0}; -y_{0}).$

Bài 6 trang 45

Cho ba điểm A(2; 2); B(3; 5), C(5; 5).

a. Tìm tọa độ điểm D sao cho ABCD là hình bình hành.

b. Tìm tọa độ giao điểm hai đường chéo của hình bình hành.

c. Giải tam giác ABC.

Gợi ý đáp án

a. Xét D(x; y). Ta có: $\vec{AB} = (1; 3); \vec{DC} = (5 - x; 5 - y)$ $\vec{AB} = (1; 3); \vec{DC} = (5 - x; 5 - y)$

Để ABCD là hình bình hành khi và chỉ khi $\vec{AB} = \vec{DC}$ $\vec{AB} = \vec{DC}$

$\Leftrightarrow \left\{\begin{matrix}5 - x = 1\\ 5 - y = 3\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} x = 4\\ y = 2\end{matrix}\right.$ $\Leftrightarrow \left\{\begin{matrix}5 - x = 1\\ 5 - y = 3\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} x = 4\\ y = 2\end{matrix}\right.$

Vậy D(4; 2)

b. Gọi M là giao điểm hai đường chéo của hình bình hành ABCD.

$\Rightarrow \left\{\begin{matrix}x_{M}= \frac{x_{A} + x_{C}}{2}\\ y_{M} = \frac{y_{A}+y_{C}}{2}\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x_{M}= \frac{2 + 5}{2}\\ y_{M} = \frac{2+5}{2}\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x_{M}= \frac{7}{2}\\ y_{M} = \frac{7}{2}\end{matrix}\right.$ $\Rightarrow \left\{\begin{matrix}x_{M}= \frac{x_{A} + x_{C}}{2}\\ y_{M} = \frac{y_{A}+y_{C}}{2}\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x_{M}= \frac{2 + 5}{2}\\ y_{M} = \frac{2+5}{2}\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x_{M}= \frac{7}{2}\\ y_{M} = \frac{7}{2}\end{matrix}\right.$

Vậy $M(\frac{7}{2}; \frac{7}{2})$ $M(\frac{7}{2}; \frac{7}{2})$

c. Ta có: $\vec{AC} = (3; 3), \vec{BC} = (2; 0)$ $\vec{AC} = (3; 3), \vec{BC} = (2; 0)$

Suy ra: $AB = |\vec{AB}| = \sqrt{1^{2} + 3^{2}} = \sqrt{10}$ $AB = |\vec{AB}| = \sqrt{1^{2} + 3^{2}} = \sqrt{10}$

$AC = |\vec{AC}| = \sqrt{3^{2} + 3^{2}} = 3\sqrt{2}$ $AC = |\vec{AC}| = \sqrt{3^{2} + 3^{2}} = 3\sqrt{2}$

$BC = |\vec{BC}| = \sqrt{2^{2} + 0^{2}} = 2$ $BC = |\vec{BC}| = \sqrt{2^{2} + 0^{2}} = 2$

$cosA = cos(\vec{AB},\vec{AC}) = \frac{\vec{AB}.\vec{AC}}{AB.AC} = \frac{1.3+3.3}{\sqrt{10}.3\sqrt{2}} = \frac{2\sqrt{5}}{5} \Rightarrow \widehat{A} \approx 26^{\circ}34$ $cosA = cos(\vec{AB},\vec{AC}) = \frac{\vec{AB}.\vec{AC}}{AB.AC} = \frac{1.3+3.3}{\sqrt{10}.3\sqrt{2}} = \frac{2\sqrt{5}}{5} \Rightarrow \widehat{A} \approx 26^{\circ}34'$

$cosB = cos(\vec{BA},\vec{BC}) = \frac{\vec{BA}.\vec{BC}}{BA.BC} = \frac{(-1).2+(-3).0}{\sqrt{10}.2} = \frac{-\sqrt{10}}{10} \Rightarrow \widehat{B} \approx 108^{\circ}26$ $cosB = cos(\vec{BA},\vec{BC}) = \frac{\vec{BA}.\vec{BC}}{BA.BC} = \frac{(-1).2+(-3).0}{\sqrt{10}.2} = \frac{-\sqrt{10}}{10} \Rightarrow \widehat{B} \approx 108^{\circ}26'$

$cosC = cos(\vec{CA},\vec{CB}) = \frac{\vec{CA}.\vec{CB}}{CA.CB} = \frac{(-3).(-2)+(-3).0}{3\sqrt{2}.2} = \frac{\sqrt{2}}{2}$ $cosC = cos(\vec{CA},\vec{CB}) = \frac{\vec{CA}.\vec{CB}}{CA.CB} = \frac{(-3).(-2)+(-3).0}{3\sqrt{2}.2} = \frac{\sqrt{2}}{2}$

Bài 7 trang 45

Cho tam giác ABC có các điểm M(2; 2), N(3; 4), P(5; 3) lần lượt là trung điểm của các cạnh AB, BC và CA.

a. Tìm tọa độ các đỉnh của tam giác ABC.

b. Chứng minh rằng trọng tâm của tam giác ABC và MNP trùng nhau.

c. Giải tam giác ABC

Gợi ý đáp án

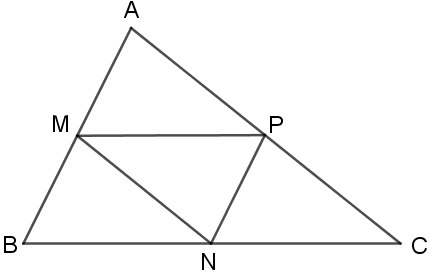
$a. \vec{MP} = (3; 1) \vec{BN} = (3 - x_{B}; 4 - y_{B})$ $a. \vec{MP} = (3; 1) \vec{BN} = (3 - x_{B}; 4 - y_{B})$

Có M là trung điểm cạnh AB, P là trung điểm cạnh AC nên MP là đường trung bình của tam giác ABC

$\Rightarrow MP // BC và MP = \frac{1}{2}BC = BN \Rightarrow MPNB$ $\Rightarrow MP // BC và MP = \frac{1}{2}BC = BN \Rightarrow MPNB$ là hình bình hành

$\Rightarrow \vec{MP} = \vec{BN}$ $\Rightarrow \vec{MP} = \vec{BN}$

$\Rightarrow \left\{\begin{matrix}3 = 3 - x_{B}\\ 1 = 4 - y_{B}\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x_{B}= 0\\ y_{B} = 3\end{matrix}\right. \Rightarrow B(0; 3)$ $\Rightarrow \left\{\begin{matrix}3 = 3 - x_{B}\\ 1 = 4 - y_{B}\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x_{B}= 0\\ y_{B} = 3\end{matrix}\right. \Rightarrow B(0; 3)$

Ta có: N là trung điểm của BC nên $\left\{\begin{matrix}x_{C}= 2x_{N} - x_{B}\\ y_{C} = 2y_{N} - y_{B}\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x_{C} = 2.3 - 0\\ y_{C} = 2.4-3 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x_{C}= 6\\ y_{C} = 5 \end{matrix}\right.$ $\left\{\begin{matrix}x_{C}= 2x_{N} - x_{B}\\ y_{C} = 2y_{N} - y_{B}\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x_{C} = 2.3 - 0\\ y_{C} = 2.4-3 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x_{C}= 6\\ y_{C} = 5 \end{matrix}\right.$

$\Rightarrow C(6; 5)$ $\Rightarrow C(6; 5)$

Ta có: M là trung điểm của AB nên $\left\{\begin{matrix}x_{A}= 2x_{M} - x_{B}\\ y_{A} = 2y_{M} - y_{B}\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x_{A} = 2.2 - 0\\ y_{A} = 2.2-3 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x_{A}= 4\\ y_{A} = 1 \end{matrix}\right.$ $\left\{\begin{matrix}x_{A}= 2x_{M} - x_{B}\\ y_{A} = 2y_{M} - y_{B}\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x_{A} = 2.2 - 0\\ y_{A} = 2.2-3 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x_{A}= 4\\ y_{A} = 1 \end{matrix}\right.$

$\Rightarrow A(4; 1)$ $\Rightarrow A(4; 1)$

Vậy A(4;1), B(0; 3), C(6; 5)

b. Gọi G là trọng tâm tam giác ABC, ta có:

$\left\{\begin{matrix}x_{G}= \frac{x_{A} + x_{B} + x_{C}}{3}\\ y_{G} = \frac{y_{A} + y_{B} + y_{C}}{3}\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x_{G}= \frac{4+0+6}{3}\\ y_{G} = \frac{1+3+5}{3}\end{matrix}\right. \left\{\begin{matrix}x_{G}= \frac{10}{3}\\ y_{G} =3\end{matrix}\right. \Rightarrow G(\frac{10}{3}; 3) (1)$ $\left\{\begin{matrix}x_{G}= \frac{x_{A} + x_{B} + x_{C}}{3}\\ y_{G} = \frac{y_{A} + y_{B} + y_{C}}{3}\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x_{G}= \frac{4+0+6}{3}\\ y_{G} = \frac{1+3+5}{3}\end{matrix}\right. \left\{\begin{matrix}x_{G}= \frac{10}{3}\\ y_{G} =3\end{matrix}\right. \Rightarrow G(\frac{10}{3}; 3) (1)$

Gọi G' là trọng tâm tam giác MNP, ta có:

$\left\{\begin{matrix}x_{G$ $\left\{\begin{matrix}x_{G'}= \frac{x_{M} + x_{N} + x_{P}}{3}\\ y_{G'} = \frac{y_{M} + y_{N} + y_{P}}{3}\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x_{G'}= \frac{2+3+5}{3}\\ y_{G'} = \frac{2+4+3}{3}\end{matrix}\right. \left\{\begin{matrix}x_{G'}= \frac{10}{3}\\ y_{G'} =3\end{matrix}\right. \Rightarrow G'(\frac{10}{3}; 3) (2)$

Từ (1) và (2) $\Rightarrow G \equiv G$ $\Rightarrow G \equiv G'$

Vậy trọng tâm tam giác ABC trùng với trọng tâm tam giác MNP.

c. Ta có $: \vec{AB} = (-4; 2); \vec{AC} = (2; 4); \vec{BC} = (6; 2)$ $: \vec{AB} = (-4; 2); \vec{AC} = (2; 4); \vec{BC} = (6; 2)$

Suy ra: $AB = |\vec{AB}| = \sqrt{(-4)^{2} + 2^{2}} = 2\sqrt{5}$ $AB = |\vec{AB}| = \sqrt{(-4)^{2} + 2^{2}} = 2\sqrt{5}$

$AC = |\vec{AC}| = \sqrt{2^{2} + 4^{2}} = 2\sqrt{5}$ $AC = |\vec{AC}| = \sqrt{2^{2} + 4^{2}} = 2\sqrt{5}$

$BC = |\vec{BC}| = \sqrt{6^{2} + 2^{2}} = 2\sqrt{10}$ $BC = |\vec{BC}| = \sqrt{6^{2} + 2^{2}} = 2\sqrt{10}$

$cosA = cos(\vec{AB}, \vec{AC}) = \frac{\vec{AB}. \vec{AC}}{AB.AC} = \frac{(-4). 2 + 2.4}{2\sqrt{5}. 2\sqrt{5}} = 0 \Rightarrow \widehat{A} = 90^{\circ}$ $cosA = cos(\vec{AB}, \vec{AC}) = \frac{\vec{AB}. \vec{AC}}{AB.AC} = \frac{(-4). 2 + 2.4}{2\sqrt{5}. 2\sqrt{5}} = 0 \Rightarrow \widehat{A} = 90^{\circ}$

Xét tam giác ABC có $AB = AC (= 2\sqrt{5}) và \widehat{A} = 90^{\circ}$ $AB = AC (= 2\sqrt{5}) và \widehat{A} = 90^{\circ}$

$\Rightarrow$ $\Rightarrow$ Tam giác ABC vuông cân tại A $\Rightarrow \widehat{B} = \widehat{C} = 45^{\circ}$ $\Rightarrow \widehat{B} = \widehat{C} = 45^{\circ}$

Bài 8 trang 45

Cho hai điểm A(1; 3), B(4; 2).

a. Tìm tọa độ điểm D nằm trên trục Ox sao cho DA = DB

b. Tính chu vi tam giác OAB.

c. Chứng minh rằng OA vuông góc với AB và từ đó tính diện tích tam giác OAB.

Gợi ý đáp án

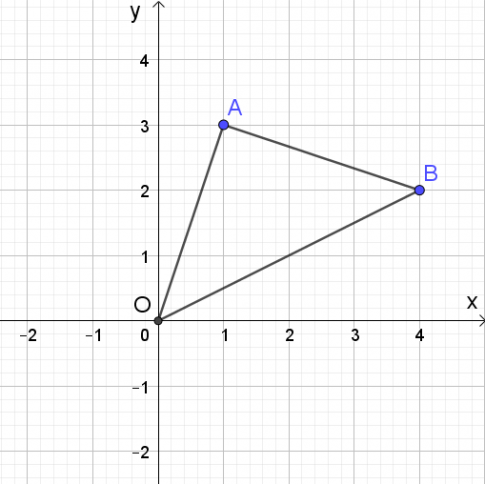
a. D nằm trên trục Ox nên D(x; 0) $\Rightarrow \vec{AD} = (x - 1; -3); \vec{BD} = (x - 4; -2)$ $\Rightarrow \vec{AD} = (x - 1; -3); \vec{BD} = (x - 4; -2)$

Ta có: $DA = DB \Rightarrow (x - 1)^{2} + (-3)^{2} = (x - 4)^{2} + (-2)^{2}$ $DA = DB \Rightarrow (x - 1)^{2} + (-3)^{2} = (x - 4)^{2} + (-2)^{2}$

$\Leftrightarrow x^{2} - 2x + 1 + 9 = x^{2} - 8x + 16 + 4 \Leftrightarrow 6x = 10 \Leftrightarrow x = \frac{5}{3}$ $\Leftrightarrow x^{2} - 2x + 1 + 9 = x^{2} - 8x + 16 + 4 \Leftrightarrow 6x = 10 \Leftrightarrow x = \frac{5}{3}$

Vậy $D(\frac{5}{3};0)$ $D(\frac{5}{3};0)$

b. Ta có: $\vec{OA} = (1; 3); \vec{OB} = (4; 2); \vec{AB} = (3; -1)$ $\vec{OA} = (1; 3); \vec{OB} = (4; 2); \vec{AB} = (3; -1)$

Suy ra: $OA = |\vec{OA}| = \sqrt{1^{2} + 3^{2}} = \sqrt{10}$ $OA = |\vec{OA}| = \sqrt{1^{2} + 3^{2}} = \sqrt{10}$

$OB = |\vec{OB}| = \sqrt{4^{2} + 2^{2}} = 2\sqrt{5}$ $OB = |\vec{OB}| = \sqrt{4^{2} + 2^{2}} = 2\sqrt{5}$

$AB = |\vec{AB}| = \sqrt{3^{2} + (-1)^{2}} = \sqrt{10}$ $AB = |\vec{AB}| = \sqrt{3^{2} + (-1)^{2}} = \sqrt{10}$

$\Rightarrow$ $\Rightarrow$Chu vi tam giác OAB là: $OA + OB + AB = \sqrt{10} + 2\sqrt{5} + \sqrt{10} = 2\sqrt{10} + 2\sqrt{5}$ $OA + OB + AB = \sqrt{10} + 2\sqrt{5} + \sqrt{10} = 2\sqrt{10} + 2\sqrt{5}$

c. Ta có: $\vec{OA}.\vec{AB} = 1. 3 + 3. (-1) = 0$ $\vec{OA}.\vec{AB} = 1. 3 + 3. (-1) = 0$

$\Rightarrow \vec{OA} \perp \vec{AB}$ $\Rightarrow \vec{OA} \perp \vec{AB}$

$\Rightarrow S_{OAB} = \frac{1}{2}OA. AB = \frac{1}{2}. \sqrt{10}. \sqrt{10} = 5$ $\Rightarrow S_{OAB} = \frac{1}{2}OA. AB = \frac{1}{2}. \sqrt{10}. \sqrt{10} = 5$

Bài 9 trang 45

Tính góc xen giữa hai vectơ $\vec{a} và \vec{b}$ $\vec{a} và \vec{b}$ trong các trường hợp sau:

$a. \vec{a} = (2; -3), \vec{b} = (6; 4)$ $a. \vec{a} = (2; -3), \vec{b} = (6; 4)$

$b. \vec{a} = (3; 2); \vec{b} = (5; -1)$ $b. \vec{a} = (3; 2); \vec{b} = (5; -1)$

$c. \vec{a} = (-2; -2\sqrt{3}), \vec{b} = (3; \sqrt{3})$ $c. \vec{a} = (-2; -2\sqrt{3}), \vec{b} = (3; \sqrt{3})$

Gợi ý đáp án

$a. cos(\vec{a}, \vec{b}) = \frac{\vec{a}.\vec{b}}{|\vec{a}|. |\vec{b}|} = \frac{2. 6 + (-3). 4}{\sqrt{2^{2} + (-3)^{2}}. \sqrt{6^{2} + 4^{2}}} = 0 \Rightarrow (\vec{a}, \vec{b}) = 90^{\circ}$ $a. cos(\vec{a}, \vec{b}) = \frac{\vec{a}.\vec{b}}{|\vec{a}|. |\vec{b}|} = \frac{2. 6 + (-3). 4}{\sqrt{2^{2} + (-3)^{2}}. \sqrt{6^{2} + 4^{2}}} = 0 \Rightarrow (\vec{a}, \vec{b}) = 90^{\circ}$

$b. cos(\vec{a}, \vec{b}) = \frac{\vec{a}.\vec{b}}{|\vec{a}|. |\vec{b}|} = \frac{3. 5 + (2. (-1)}{\sqrt{3^{2} + 2^{2}}. \sqrt{5^{2} + (-1)^{2}}} = \frac{\sqrt{2}}{2} \Rightarrow (\vec{a}, \vec{b}) = 45^{\circ}$ $b. cos(\vec{a}, \vec{b}) = \frac{\vec{a}.\vec{b}}{|\vec{a}|. |\vec{b}|} = \frac{3. 5 + (2. (-1)}{\sqrt{3^{2} + 2^{2}}. \sqrt{5^{2} + (-1)^{2}}} = \frac{\sqrt{2}}{2} \Rightarrow (\vec{a}, \vec{b}) = 45^{\circ}$

$c. cos(\vec{a}, \vec{b}) = \frac{\vec{a}.\vec{b}}{|\vec{a}|. |\vec{b}|} = \frac{(-2).3 + (-2\sqrt{3}).\sqrt{3}}{\sqrt{(-2)^{2} + (-2\sqrt{3})^{2}}. \sqrt{3^{2} + (\sqrt{3})^{2}}} = \frac{-\sqrt{3}}{2} \Rightarrow (\vec{a}, \vec{b}) = 150^{\circ}$ $c. cos(\vec{a}, \vec{b}) = \frac{\vec{a}.\vec{b}}{|\vec{a}|. |\vec{b}|} = \frac{(-2).3 + (-2\sqrt{3}).\sqrt{3}}{\sqrt{(-2)^{2} + (-2\sqrt{3})^{2}}. \sqrt{3^{2} + (\sqrt{3})^{2}}} = \frac{-\sqrt{3}}{2} \Rightarrow (\vec{a}, \vec{b}) = 150^{\circ}$

Bài 10 trang 45

Cho bốn điểm A(7; -3), B(8; 4), C(1; 5), D(0; -2). Chứng minh rằng tứ giác ABCD là hình vuông.

Gợi ý đáp án

Ta có: $\vec{AB} = (1; 7), \vec{DC} = (1; 7); \vec{AD} = (-7; 1)$ $\vec{AB} = (1; 7), \vec{DC} = (1; 7); \vec{AD} = (-7; 1)$

Nhận thấy: $\vec{AB} = \vec{DC} \Rightarrow$ $\vec{AB} = \vec{DC} \Rightarrow$ ABCD là hình bình hành

mà $|\vec{AB}| = |\vec{AD}|$ $|\vec{AB}| = |\vec{AD}|$ (vì cùng = $5\sqrt{2}$ $5\sqrt{2}$) hay AB = AD $\Rightarrow$ $\Rightarrow$ ABCD là hình thoi (1)

Ta có: $\vec{AB}. \vec{AD} = 1. (-7) + 7. 1 = 0 \Rightarrow \vec{AB} \perp \vec{AD} \Rightarrow AB \perp AD (2)$ $\vec{AB}. \vec{AD} = 1. (-7) + 7. 1 = 0 \Rightarrow \vec{AB} \perp \vec{AD} \Rightarrow AB \perp AD (2)$

Từ (1) và (2) $\Rightarrow$ $\Rightarrow$ ABCD là hình vuông (đpcm)

Bài 11 trang 45

Một máy bay đang hạ cánh với vận tốc $\vec{v} = (-210; -42).$ $\vec{v} = (-210; -42).$ Cho biết vận tốc của gió là $\vec{w} = (-12; -4)$ $\vec{w} = (-12; -4)$ và một đơn vị trên hệ trục tọa độ tương ứng với 1 km. Tìm độ dài vectơ tổng hai vận tốc $\vec{v} và \vec{w}$ $\vec{v} và \vec{w}$

Gợi ý đáp án

Ta có: $\vec{v} + \vec{w} = (-210 + (-12); -42 + (-4))= (-222; -46)$ $\vec{v} + \vec{w} = (-210 + (-12); -42 + (-4))= (-222; -46)$

Độ dài của vectơ tổng hai vận tốc $\vec{v} và \vec{w}$ $\vec{v} và \vec{w}$ là:

$|\vec{v} + \vec{w}| = \sqrt{(-222)^{2} + (-46)^{2}} = 10\sqrt{514} (km)$ $|\vec{v} + \vec{w}| = \sqrt{(-222)^{2} + (-46)^{2}} = 10\sqrt{514} (km)$

Lý thuyết Tọa độ của vectơ

1. Toạ độ của vectơ đối với một hệ trục toạ độ

Mặt phẳng mà trên đó đã cho một hệ trục toạ độ Oxy được gọi là mặt phẳng toa độ Oxy, hay gọi tắt là mặt phẳng Oxy.

*Toạ độ của một vectơ

Trong mặt phẳng Oxy, cặp số (x; y) trong biểu diễn $\overrightarrow a = x\overrightarrow i + y\overrightarrow j$ $\overrightarrow a = x\overrightarrow i + y\overrightarrow j$ được gọi là toạ độ của vectơ $\overrightarrow a$ $\overrightarrow a$. kí hiệu $\overrightarrow a$ $\overrightarrow a$ = (x, y), x gọi là hoành độ, y gọi là tung độ của vectơ $\overrightarrow a$ $\overrightarrow a$.

Chú ý:

+ $\overrightarrow a = \left( {x,y} \right) \Leftrightarrow \overrightarrow a = x\overrightarrow i + y\overrightarrow j$ $\overrightarrow a = \left( {x,y} \right) \Leftrightarrow \overrightarrow a = x\overrightarrow i + y\overrightarrow j$

+ Nếu cho $\overrightarrow a = \left( {x,y} \right) và \overrightarrow b = \left( {x$ $\overrightarrow a = \left( {x,y} \right) và \overrightarrow b = \left( {x',y'} \right)$ thì $\overrightarrow a = \overrightarrow b \Leftrightarrow \left\{ \begin{array}{l} x = x$ $\overrightarrow a = \overrightarrow b \Leftrightarrow \left\{ \begin{array}{l} x = x'\\ y = y' \end{array} \right.$

*Toạ độ của một điểm

Trong mặt phẳng toa độ, cho một điểm M tuỳ ý. Toạ độ của vectơ $\overrightarrow {OM}$ $\overrightarrow {OM}$ được gọi là toạ độ của điểm M.

Nhận xét:

+ Nếu $\overrightarrow {OM} = \left( {x;y} \right)$ $\overrightarrow {OM} = \left( {x;y} \right)$ thì cặp số (x; y) là toa độ của điểm M, kí hiệu M(x; y), x gọi là hoành độ, y gọi là tung độ của điểm M

+ $M\left( {x;y} \right) \Leftrightarrow \overrightarrow {OM} = x\overrightarrow i + y\overrightarrow j$ $M\left( {x;y} \right) \Leftrightarrow \overrightarrow {OM} = x\overrightarrow i + y\overrightarrow j$

Chú ý: Hoành độ của điểm M còn được kí hiệu là x_M, tung độ của điểm M còn được kí hiệu là y_M. Khi đó ta việt M(x_M; y_M).

2. Biểu thức toạ độ của các phép toán vectơ

Cho hai vectơ $\overrightarrow a = \left( {{a_1};{a_2}} \right),\overrightarrow b = \left( {{b_1};{b_2}} \right)$ $\overrightarrow a = \left( {{a_1};{a_2}} \right),\overrightarrow b = \left( {{b_1};{b_2}} \right)$ và số thực k. Khi đó:

$\begin{array}{l} 1)\;\;\;\overrightarrow a + \overrightarrow b = \left( {{a_1} + {b_1};{a_2} + {b_2}} \right);\\ 2)\;\;\;\overrightarrow a - \overrightarrow b = \left( {{a_1} - {b_1};{a_2} - {b_2}} \right);\\ 3)\;\;\;k\overrightarrow a = \left( {k{a_1};k{a_2}} \right);\\ 4)\;\;\;\overrightarrow a .\overrightarrow b = {a_1}.{b_1} + {a_2}.{b_2}. \end{array}$ $\begin{array}{l} 1)\;\;\;\overrightarrow a + \overrightarrow b = \left( {{a_1} + {b_1};{a_2} + {b_2}} \right);\\ 2)\;\;\;\overrightarrow a - \overrightarrow b = \left( {{a_1} - {b_1};{a_2} - {b_2}} \right);\\ 3)\;\;\;k\overrightarrow a = \left( {k{a_1};k{a_2}} \right);\\ 4)\;\;\;\overrightarrow a .\overrightarrow b = {a_1}.{b_1} + {a_2}.{b_2}. \end{array}$

Ví dụ: Cho hai vectơ $\overrightarrow a = \left( {1;5} \right),\overrightarrow b = \left( {4; - 2} \right)$ $\overrightarrow a = \left( {1;5} \right),\overrightarrow b = \left( {4; - 2} \right)$. Tìm toạ độ của các vectơ $\overrightarrow a + \overrightarrow b ,\overrightarrow a - \overrightarrow b ,3\overrightarrow a , - 5\overrightarrow b$ $\overrightarrow a + \overrightarrow b ,\overrightarrow a - \overrightarrow b ,3\overrightarrow a , - 5\overrightarrow b$

Giải

$\begin{array}{l} \overrightarrow a + \overrightarrow b = \left( {1 + 4;5 + \left( { - 2} \right)} \right) = \left( {5;3} \right);\\ \overrightarrow a - \overrightarrow b = \left( {1 - 4;5 - \left( { - 2} \right)} \right) = \left( { - 3;7} \right);\\ 3\overrightarrow a = \left( {3.1;3.5} \right) = \left( {3;15} \right);\\ - 5.\overrightarrow b = \left( { - 5.4; - 5.\left( { - 2} \right)} \right) = \left( { - 20;10} \right) \end{array}$ $\begin{array}{l} \overrightarrow a + \overrightarrow b = \left( {1 + 4;5 + \left( { - 2} \right)} \right) = \left( {5;3} \right);\\ \overrightarrow a - \overrightarrow b = \left( {1 - 4;5 - \left( { - 2} \right)} \right) = \left( { - 3;7} \right);\\ 3\overrightarrow a = \left( {3.1;3.5} \right) = \left( {3;15} \right);\\ - 5.\overrightarrow b = \left( { - 5.4; - 5.\left( { - 2} \right)} \right) = \left( { - 20;10} \right) \end{array}$

Chia sẻ bởi: