Toán 10 Bài 2: Hàm số bậc hai Giải SGK Toán 10 trang 56, 57 - Tập 1 sách Chân trời sáng tạo

Giới thiệu Tải về Bình luận

Toán 10 Bài 2 Chân trời sáng tạo trang 56, 57 giúp các bạn học sinh có thêm nhiều gợi ý tham khảo để trả lời các câu hỏi phần Hoạt động và bài tập trong SGK bài Hàm số bậc hai.

Giải Toán 10 Chân trời sáng tạo bài 2 trang 56, 57 được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa môn Toán 10 tập 1. Giải Toán 10 bài 2 Chân trời sáng tạo là tài liệu cực kì hữu ích hỗ trợ các em học sinh lớp 10 trong quá trình giải bài tập. Đồng thời phụ huynh có thể sử dụng để hướng dẫn con em học tập và đổi mới phương pháp giải phù hợp hơn. Vậy sau đây là nội dung chi tiết giải Toán 10 Bài 2 Hàm số bậc hai mời các bạn cùng theo dõi.

Toán 10 Bài 2: Hàm số bậc hai

Trả lời câu hỏi Hoạt động Toán 10 Bài 2 trang 49

Hoạt động 1

Khai triển biểu thức của các hàm số sau và sắp xếp theo thứ tự lũy thừa của x giảm dần (nếu có thể). Hàm số nào có lũy thừa bậc cao nhất của x là bậc hai?

a) y = 2x(x – 3)

b) y = x(x²+ 2) – 5

c) y = -5(x + 1)(x – 4)

Gợi ý đáp án

a) Xét hàm số: y = 2x(x – 3) = 2x²– 6x

Bậc cao nhất của hàm số là bậc hai

b) Xét hàm số: y = x(x²+ 2) – 5 = x³+ 2x – 5

Bậc cao nhất của hàm số là bậc ba

c) y = -5(x + 1)(x – 4) = - 5x²+ 15x + 20

Bậc cao nhất của hàm số là bậc hai

Vậy hàm số ở ý a) và c) là các số có lũy thừa bậc cao nhất của x là bậc hai.

Hoạt động 2

a) Xét hàm số: y = f(x) = x² – 8x + 19 = (x – 4)² + 3 có bảng giá trị:

x	2	3	4	5	6
f(x)	7	4	3	4	7

Trên mặt phẳng tọa độ, ta có các điểm (x; f(x)) với x thuộc bảng giá trị đã cho (Hình 1).

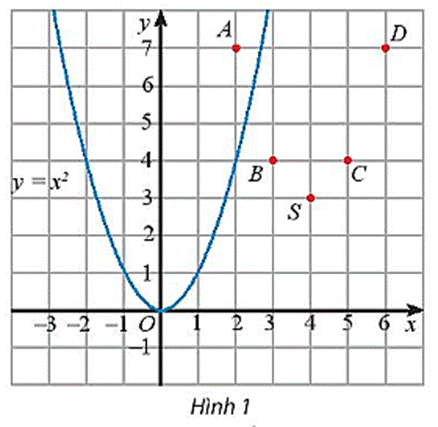
Hãy vẽ đường cong đi qua các điểm A, B, S, C, D và nêu nhận xét về hình dạng của đường cong này so với đồ thị của hàm số y = x² trên Hình 1.

b) Tương tự, xét hàm số: y = g(x) = - x²+ 8x – 13 = - (x – 4)²+ 3 có bảng giá trị:

x	2	3	4	5	6
g(x)	-1	2	3	2	-1

Trên mặt phẳng tọa độ, ta có các điểm (x; g(x)) với x thuộc bảng giá trị đã cho (Hình 2).

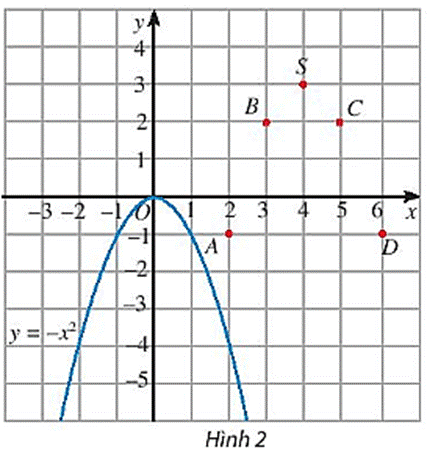
Hãy vẽ đường cong đi qua các điểm A, B, S, C, D và nêu nhận xét về hình dạng của đường cong này so với đồ thị hàm số y = - x² trên Hình 2.

Lời giải chi tiết

a) Đường cong đi qua các điểm A, B, S, C, D là đường cong màu đỏ trên hình vẽ:

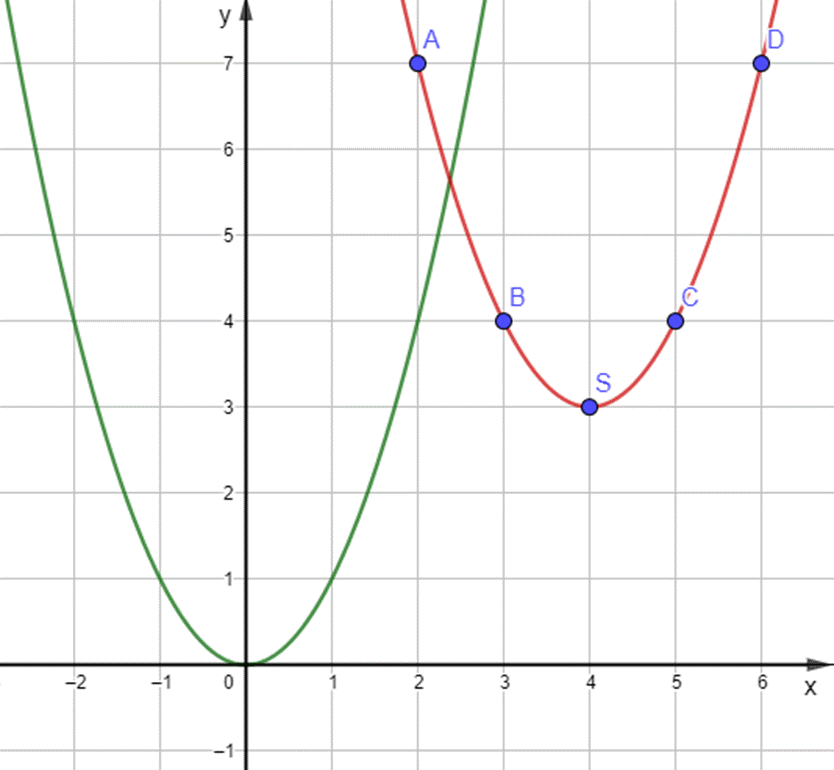
Nhận xét:

Về hình dáng của đường cong màu đỏ giống với hình dáng của đường cong màu xanh là một đường cong parabol.

- Có đỉnh là điểm S với hoành độ là 4 và tung độ là 3.

- Có trục đối xứng là đường thẳng x = 4 (đường thẳng này đi qua đỉnh S và song song với trục Oy).

- Bề lõm của đồ thị hướng lên trên.

b) Đường cong đi qua các điểm A, B, S, C, D là đường cong màu cam trên hình vẽ:

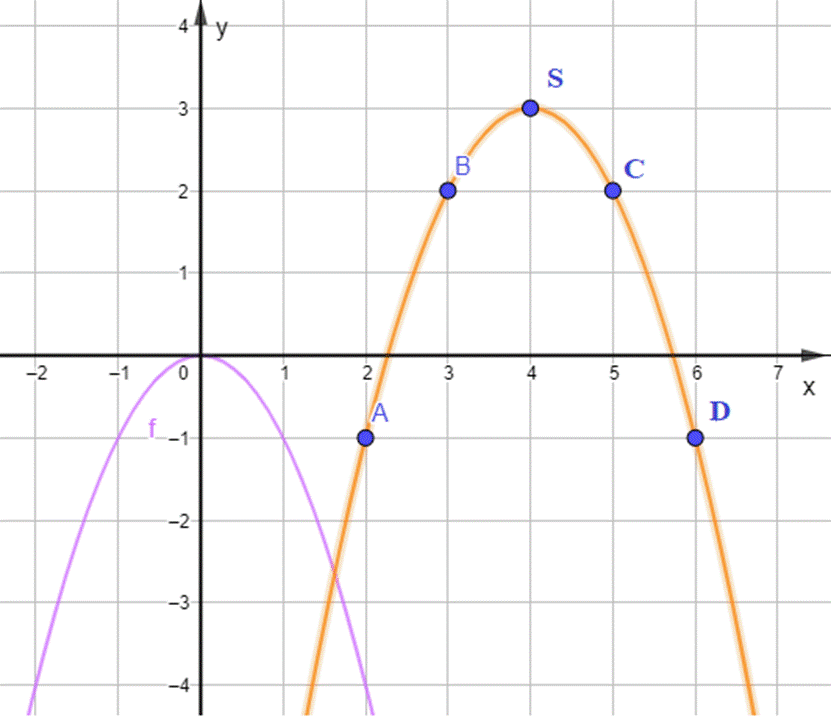
Nhận xét:

Về hình dáng của đường cong màu cam giống với hình dáng của đường cong màu tím là một đường cong parabol.

- Có đỉnh là điểm S với hoành độ là 4 và tung độ là 3.

- Có trục đối xứng là đường thẳng x = 4 (đường thẳng này đi qua đỉnh S và song song với trục Oy).

- Bề lõm của đồ thị hướng xuống dưới.

Giải Toán 10 trang 56, 57 Chân trời sáng tạo - Tập 1

Bài 1 trang 56

Hàm số nào sau đây là hàm số bậc hai?

a) $y = 9{x^2} + 5x + 4$ $y = 9{x^2} + 5x + 4$

$b) y = 3{x^3} + 2x + 1$ $b) y = 3{x^3} + 2x + 1$

$c) y = - 4{(x + 2)^2} + 2(2{x^3} + 1) + x + 4$ $c) y = - 4{(x + 2)^2} + 2(2{x^3} + 1) + x + 4$

$d) y = 5{x^2} + \sqrt x + 2$ $d) y = 5{x^2} + \sqrt x + 2$

Gợi ý đáp án

Hàm số ở câu a) $y = 9{x^2} + 5x + 4$ $y = 9{x^2} + 5x + 4$ là hàm số bậc hai với a = 9,b = 5,c = 4

Hàm số ở câu b), c) không phải là hàm số bậc hai vì chứa ${x^3}$ ${x^3}$

Hàm số ở câu d) $y = 5{x^2} + \sqrt x + 2$ $y = 5{x^2} + \sqrt x + 2$ không phải là hàm số bậc hai vì chứa $\sqrt x$ $\sqrt x$

Bài 2 trang 56

Tìm điều kiện của m để mỗi hàm số sau là hàm số bậc hai:

$a) y = m{x^4} + (m + 1){x^2} + x + 3$ $a) y = m{x^4} + (m + 1){x^2} + x + 3$

$b) y = (m - 2){x^3} + (m - 1){x^2} + 5$ $b) y = (m - 2){x^3} + (m - 1){x^2} + 5$

Gợi ý đáp án

a) Để hàm số $y = m{x^4} + (m + 1){x^2} + x + 3$ $y = m{x^4} + (m + 1){x^2} + x + 3$ là hàm số bậc hai thì:

$\left\{ \begin{array}{l}m = 0\\m + 1 \ne 0\end{array} \right.$ $\left\{ \begin{array}{l}m = 0\\m + 1 \ne 0\end{array} \right.$ tức là m = 0.

Khi đó $y = {x^2} + x + 3$ $y = {x^2} + x + 3$

Vây m = 0 thì hàm số đã cho là hàm số bậc hai $y = {x^2} + x + 3$ $y = {x^2} + x + 3$

b) Để hàm số $y = (m - 2){x^3} + (m - 1){x^2} + 5$ $y = (m - 2){x^3} + (m - 1){x^2} + 5$ là hàm số bậc hai thì:

$\left\{ \begin{array}{l}m - 2 = 0\\m - 1 \ne 0\end{array} \right.$ $\left\{ \begin{array}{l}m - 2 = 0\\m - 1 \ne 0\end{array} \right.$ tức là m = 2.

Khi đó $y = (2 - 1){x^2} + 5 = {x^2} + 5$ $y = (2 - 1){x^2} + 5 = {x^2} + 5$

Vây m = 2 thì hàm số đã cho là hàm số bậc hai $y = {x^2} + 5$ $y = {x^2} + 5$

Bài 3 trang 56

Lập bảng biến thiên của hàm số $y = {x^2} + 2x + 3$ $y = {x^2} + 2x + 3$. Hàm số này có giá trị lớn nhất hay giá trị nhỏ nhất? Tìm giá trị đó.

Gợi ý đáp án

Đỉnh S có tọa độ: ${x_S} = \dfrac{{ - b}}{{2a}} = \dfrac{{ - 2}}{{2.1}} = - 1;\,{y_S} = {\left( { - 1} \right)^2} + 2.( - 1) + 3 = 2.$ ${x_S} = \dfrac{{ - b}}{{2a}} = \dfrac{{ - 2}}{{2.1}} = - 1;\,{y_S} = {\left( { - 1} \right)^2} + 2.( - 1) + 3 = 2.$

Hay $S\left( { - 1;2} \right).$ $S\left( { - 1;2} \right).$

Vì hàm số bậc hai có a = 1 > 0 nên ta có bảng biến thiên sau:

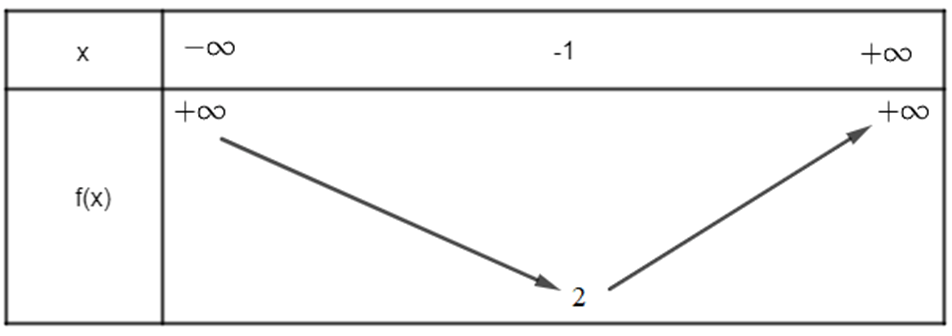
Hàm số đạt giá trị nhỏ nhất bằng 2.

Bài 4 trang 56

Cho hàm số bậc hai $y = f(x) = a{x^2} + bx + c có f(0) = 1,f(1) = 2,f(2) = 5$ $y = f(x) = a{x^2} + bx + c có f(0) = 1,f(1) = 2,f(2) = 5$.

a) Hãy xác định giá trị của các hệ số a,b và c.

b) Xác định tập giá trị và khoảng biến thiên của hàm số.

Gợi ý đáp án

a) Ta có: $f(0) = a{.0^2} + b.0 + c = 1 \Rightarrow c = 1.$ $f(0) = a{.0^2} + b.0 + c = 1 \Rightarrow c = 1.$

Lại có:

$f(1) = a{.1^2} + b.1 + c = 2 \Rightarrow a + b + 1 = 2$ $f(1) = a{.1^2} + b.1 + c = 2 \Rightarrow a + b + 1 = 2$

$f(2) = a{.2^2} + b.2 + c = 5 \Rightarrow 4a + 2b + 1 = 5$ $f(2) = a{.2^2} + b.2 + c = 5 \Rightarrow 4a + 2b + 1 = 5$

Từ đó ta có hệ phương trình $\left\{ \begin{array}{l}a + b + 1 = 2\\4a + 2b + 1 = 5\end{array} \right.$ $\left\{ \begin{array}{l}a + b + 1 = 2\\4a + 2b + 1 = 5\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}a + b = 1\\4a + 2b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 0\end{array} \right.(thỏa mãn điều kiện a \ne 0)$ $\Leftrightarrow \left\{ \begin{array}{l}a + b = 1\\4a + 2b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 0\end{array} \right.(thỏa mãn điều kiện a \ne 0)$

Vậy hàm số bậc hai đó là $y = f(x) = {x^2} + 1$ $y = f(x) = {x^2} + 1$

b) Tập giá trị $T = \{ {x^2} + 1|x \in \mathbb{R}\}$ $T = \{ {x^2} + 1|x \in \mathbb{R}\}$

Vì {x^2} + 1 \ge 1\;\forall x \in \mathbb{R} nên T = [1; + \infty )

Đỉnh S có tọa độ: ${x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 0}}{{2.1}} = 0;{y_S} = f(0) = 1$ ${x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 0}}{{2.1}} = 0;{y_S} = f(0) = 1$

Hay S\left( {0;1} \right).

Vì hàm số bậc hai có a = 1 > 0 nên ta có bảng biến thiên sau:

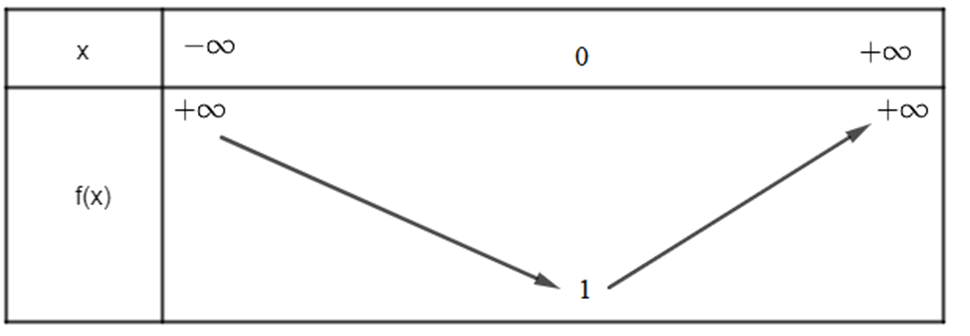
Hàm số nghịch biến trên khoảng $\left( { - \infty ;0} \right)$ $\left( { - \infty ;0} \right)$ và đồng biến trên khoảng $\left( {0; + \infty } \right)$ $\left( {0; + \infty } \right)$

Bài 5 trang 56

Cho hàm số $y = 2{x^2} + x + m.$ $y = 2{x^2} + x + m.$ Hãy xác định giá trị của m để hàm số đạt giá trị nhỏ nhất bằng 5.

Gợi ý đáp án

Đỉnh S có tọa độ: ${x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 1}}{{2.2}} = - \frac{1}{4};{y_S} = f( - \frac{1}{4}) = 2{\left( { - \frac{1}{4}} \right)^2} + \left( { - \frac{1}{4}} \right) + m = m - \frac{1}{8}$ ${x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 1}}{{2.2}} = - \frac{1}{4};{y_S} = f( - \frac{1}{4}) = 2{\left( { - \frac{1}{4}} \right)^2} + \left( { - \frac{1}{4}} \right) + m = m - \frac{1}{8}$

Ta có: a = 2 > 0, hàm số có bảng biến thiên dạng:

Hàm số đạt giá trị nhỏ nhất bằng $m - \frac{1}{8} = 5 \Leftrightarrow m = \frac{{41}}{8}.$ $m - \frac{1}{8} = 5 \Leftrightarrow m = \frac{{41}}{8}.$

Vậy $m = \frac{{41}}{8}$ $m = \frac{{41}}{8}$ thì hàm số đạt giá trị nhỏ nhất bằng 5.

Bài 6 trang 56

Vẽ đồ thị các hàm số sau:

$a) y = 2{x^2} + 4x - 1$ $a) y = 2{x^2} + 4x - 1$

$b) y = - {x^2} + 2x + 3$ $b) y = - {x^2} + 2x + 3$

$c) y = - 3{x^2} + 6x$ $c) y = - 3{x^2} + 6x$

$d) y = 2{x^2} - 5$ $d) y = 2{x^2} - 5$

Gợi ý đáp án

$a) y = 2{x^2} + 4x - 1$ $a) y = 2{x^2} + 4x - 1$

Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai $y = 2{x^2} + 4x - 1$ $y = 2{x^2} + 4x - 1$ là một parabol (P):

+ Có đỉnh S với hoành độ: ${x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 4}}{{2.2}} = - 1;{y_S} = 2.{( - 1)^2} + 4.( - 1) - 1 = - 3.$ ${x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 4}}{{2.2}} = - 1;{y_S} = 2.{( - 1)^2} + 4.( - 1) - 1 = - 3.$

+ Có trục đối xứng là đường thẳng x = - 1 (đường thẳng này đi qua đỉnh S và song song với trục Oy);

+ Bề lõm quay lên trên vì a = 2 > 0

+ Cắt trục tung tại điểm có tung độ bằng -1, tức là đồ thị đi qua điểm có tọa độ (0; -1).

Ta vẽ được đồ thị như hình dưới.

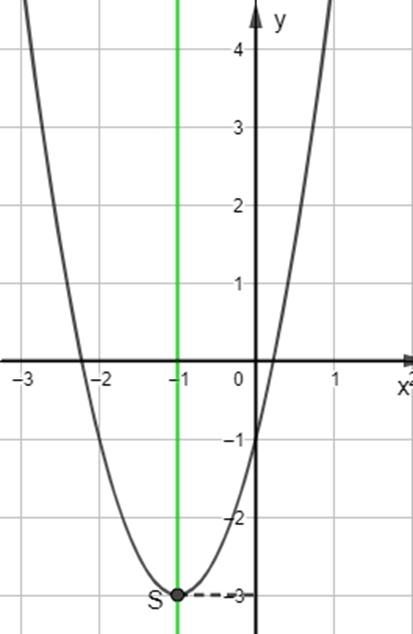
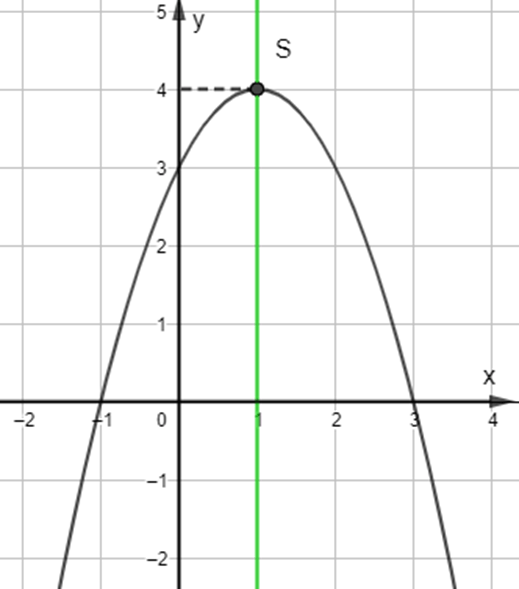
$b) y = - {x^2} + 2x + 3$ $b) y = - {x^2} + 2x + 3$

Gợi ý đáp án:

Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai $y = - {x^2} + 2x + 3$ $y = - {x^2} + 2x + 3$ là một parabol (P):

+ Có đỉnh S với hoành độ: ${x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 2}}{{2.( - 1)}} = 1;{y_S} = - {1^2} + 2.1 + 3 = 4.$ ${x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 2}}{{2.( - 1)}} = 1;{y_S} = - {1^2} + 2.1 + 3 = 4.$

+ Có trục đối xứng là đường thẳng x = 1 (đường thẳng này đi qua đỉnh S và song song với trục Oy);

+ Bề lõm quay xuống dưới vì a = - 1 < 0

+ Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).

Ta vẽ được đồ thị như hình dưới.

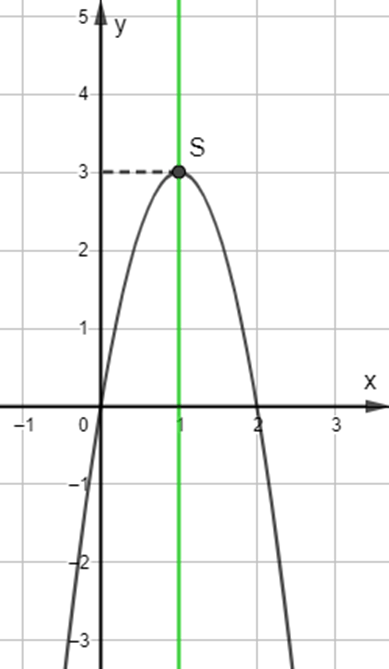
$c) y = - 3{x^2} + 6x$ $c) y = - 3{x^2} + 6x$

Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai $y = - 3{x^2} + 6x$ $y = - 3{x^2} + 6x$ là một parabol (P):

+ Có đỉnh S với hoành độ: ${x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 6}}{{2.( - 3)}} = 1;{y_S} = - {3.1^2} + 6.1 = 3$ ${x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 6}}{{2.( - 3)}} = 1;{y_S} = - {3.1^2} + 6.1 = 3$

+ Có trục đối xứng là đường thẳng x = 1 (đường thẳng này đi qua đỉnh S và song song với trục Oy);

+ Bề lõm quay xuống dưới vì a = - 3 < 0

+ Cắt trục tung tại điểm có tung độ bằng 0, tức là đồ thị đi qua gốc tọa độ (0; 0).

Ta vẽ được đồ thị như hình dưới.

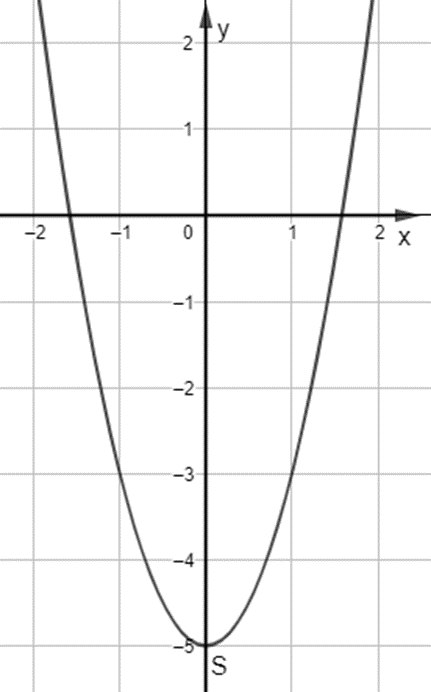
$d) y = 2{x^2} - 5$ $d) y = 2{x^2} - 5$

Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai $y = 2{x^2} - 5$ $y = 2{x^2} - 5$ là một parabol (P):

+ Có đỉnh S với hoành độ: ${x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 0}}{{2.2}} = 0;{y_S} = {2.0^2} - 5 = - 5.$ ${x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 0}}{{2.2}} = 0;{y_S} = {2.0^2} - 5 = - 5.$

+ Có trục đối xứng là đường thẳng x = 0 (trùng với trục Oy);

+ Bề lõm quay lên trên vì a = 2 > 0

+ Cắt trục tung tại điểm có tung độ bằng -5, tức là đồ thị đi qua điểm có tọa độ (0; -5).

Ta vẽ được đồ thị như hình dưới.

Bài 7 trang 56

Hãy xác định đúng đồ thị của mỗi hàm số sau trên Hình 12.

Gợi ý đáp án

Vì 4 đồ thị hàm số cắt trục tung tại 4 điểm phân biệt nên ta chỉ cần xác định tọa độ giao điểm của mỗi hàm số với trục tung là có thể phân biệt 4 đồ thị hàm số.

Đồ thị hàm số $({P_1}):y = - 2{x^2} - 4x + 2$ $({P_1}):y = - 2{x^2} - 4x + 2$ cắt trục tung tại điểm có tung độ bằng 2, tức là đồ thị đi qua điểm có tọa độ (0; 2) => Đồ thị là đường màu xanh lá.

Đồ thị hàm số $({P_2}):y = 3{x^2} - 6x + 5$ $({P_2}):y = 3{x^2} - 6x + 5$; cắt trục tung tại điểm có tung độ bằng 5, tức là đồ thị đi qua điểm có tọa độ (0; 5) => Đồ thị là đường màu xanh dương.

Đồ thị hàm số $({P_3}):y = 4{x^2} - 8x + 7$ $({P_3}):y = 4{x^2} - 8x + 7$; cắt trục tung tại điểm có tung độ bằng 7, tức là đồ thị đi qua điểm có tọa độ (0; 7) => Đồ thị là đường màu nâu đỏ.

Đồ thị hàm số $({P_4}):y = - 3{x^2} - 6x - 1$ $({P_4}):y = - 3{x^2} - 6x - 1$ cắt trục tung tại điểm có tung độ bằng -1, tức là đồ thị đi qua điểm có tọa độ (0; -1) => Đồ thị là đường màu vàng.

Bài 8 trang 56

Tìm công thức của hàm số bậc hai có đồ thị như Hình 13.

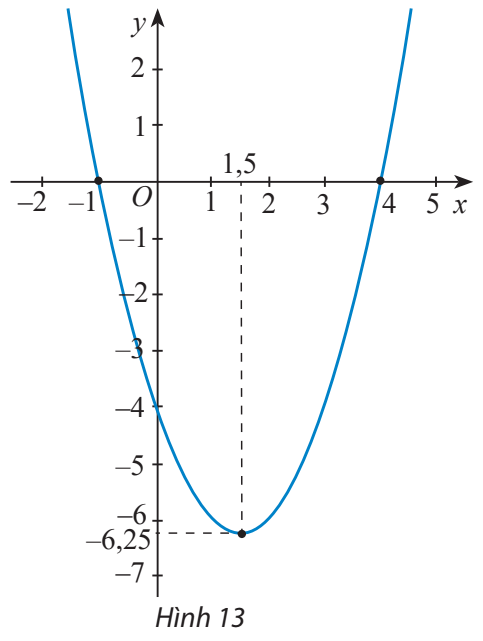
Gợi ý đáp án

Gọi công thức của hàm số bậc hai là $y = a{x^2} + bx + c$ $y = a{x^2} + bx + c$

Đồ thị hàm số đi qua 3 điểm có tọa độ (-1;0), (4;0), (0;-4)

$\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}a.{( - 1)^2} + b.( - 1) + c = 0\\a{.4^2} + b.4 + c = 0\\a{.0^2} + b.0 + c = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a - b + c = 0\\16a + 4b + c = 0\\c = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a - b = 4\\16a + 4b = 4\\c = - 4\end{array} \right.\\ \Leftrightarrow a = 1,b = - 3,c = - 4.\end{array}$ $\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}a.{( - 1)^2} + b.( - 1) + c = 0\\a{.4^2} + b.4 + c = 0\\a{.0^2} + b.0 + c = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a - b + c = 0\\16a + 4b + c = 0\\c = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a - b = 4\\16a + 4b = 4\\c = - 4\end{array} \right.\\ \Leftrightarrow a = 1,b = - 3,c = - 4.\end{array}$

Vậy hàm số cần tìm có công thức $y = {x^2} - 3x - 4$ $y = {x^2} - 3x - 4$

Bài 9 trang 56

Chiếc cầu dây văng một nhịp được thiết kế hai bên thành cầu có dạng parabol và được cố định bằng các dây cáp song song.

Dựa vào bản vẽ ở Hình 14, hãy tính chiều dài tổng cộng của các dây cáp dọc ở hai mặt bên. Biết:

- Dây dài nhất là 5 m, dây ngắn nhất là 0,8 m. Khoảng cách giữa các dây bằng nhau.

- Nhịp cầu dài 30 m.

- Cần tính thêm 5% chiều dài mỗi sợi dây cáp để neo cố định.

Gợi ý đáp án

Gọi $y = a{x^2} + bx + c$ $y = a{x^2} + bx + c$ là công thức của hàm số có đồ thị là thành cầu.

Chọn hệ trục tọa độ Oxy như hình dưới:

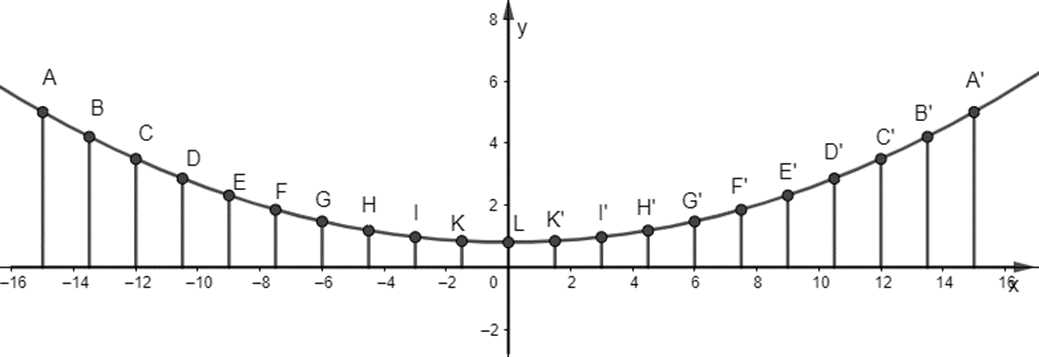
Khi đó độ dài dây cáp dọc ở mỗi mặt bên là tung độ của điểm biểu diễn tương ứng.

Ở mỗi mặt: có 21 dây cáp dọc, tương ứng cho 20 khoảng cách giữa chúng.

Khoảng cách giữa hai dây cáp liền kề là: $30:20 = 1,5\left( m \right)$ $30:20 = 1,5\left( m \right)$

Khi đó: ${x_0} = 0;{x_1} = 1,5;\;{x_2} = 3;\;{x_3} = 4,5;\;...;{x_n} = 1,5.n\;$ ${x_0} = 0;{x_1} = 1,5;\;{x_2} = 3;\;{x_3} = 4,5;\;...;{x_n} = 1,5.n\;$

Dễ thấy: các điểm có tọa độ $(0; 5), ({x_{10}};0,8), ({x_{20}};5)$ $(0; 5), ({x_{10}};0,8), ({x_{20}};5)$ thuộc đồ thị hàm số.

(Trong đó: ${x_{10}} = 10.1,5 = 15;\;{x_{20}} = 20.1,5 = 30.)$ ${x_{10}} = 10.1,5 = 15;\;{x_{20}} = 20.1,5 = 30.)$

Suy ra:

$f(0) = a{.0^2} + b.0 + c = 5 \Leftrightarrow c = 5$ $f(0) = a{.0^2} + b.0 + c = 5 \Leftrightarrow c = 5$

Và $f(1) = a{.10^2} + b.10 + c = 0,8 \Leftrightarrow 100a + 10b + 5 = 0,8$ $f(1) = a{.10^2} + b.10 + c = 0,8 \Leftrightarrow 100a + 10b + 5 = 0,8$

$f(2) = a{.30^2} + b.30 + c = 5 \Leftrightarrow 900a + 30b + 5 = 5$ $f(2) = a{.30^2} + b.30 + c = 5 \Leftrightarrow 900a + 30b + 5 = 5$

Giải hệ phương trình $\left\{ \begin{array}{l}100a + 10b + 5 = 0,8\\900a + 30b + 5 = 5\end{array} \right.$ $\left\{ \begin{array}{l}100a + 10b + 5 = 0,8\\900a + 30b + 5 = 5\end{array} \right.$ ta được $a = \frac{{21}}{{1000}};b = - \frac{{63}}{{100}}$ $a = \frac{{21}}{{1000}};b = - \frac{{63}}{{100}}$

Như vậy $y = \frac{{21}}{{1000}}{x^2} - \frac{{63}}{{100}}x + 5$ $y = \frac{{21}}{{1000}}{x^2} - \frac{{63}}{{100}}x + 5$

Gọi ${y_0},{y_1},{y_2},..{y_{20}}$ ${y_0},{y_1},{y_2},..{y_{20}}$ là tung độ của các điểm có hoành độ lần lượt là ${x_0},{x_1},{x_2},..{x_{20}}$ ${x_0},{x_1},{x_2},..{x_{20}}$

Ta có:

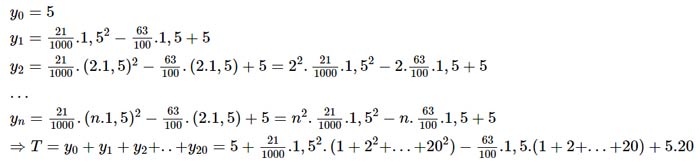
Mà $1 + {2^2} + ... + {20^2} = 2870;\;1 + 2 + ... + 20 = 210$ $1 + {2^2} + ... + {20^2} = 2870;\;1 + 2 + ... + 20 = 210$

$\Rightarrow T = 5 + \frac{{21}}{{1000}}.1,{5^2}.2870 - \frac{{63}}{{100}}.1,5.210 + 5.20 \approx 42,16(m)$ $\Rightarrow T = 5 + \frac{{21}}{{1000}}.1,{5^2}.2870 - \frac{{63}}{{100}}.1,5.210 + 5.20 \approx 42,16(m)$

Tổng chiều dài của các dây cáp dọc ở hai mặt bên là: 42,16.2 = 84,32(m)

Vậy chiều dài tổng cộng của các dây cáp dọc ở hai mặt bên là 84,32m.

Lý thuyết Hàm số bậc hai

1. Hàm số bậc hai

+ Định nghĩa:

Hàm số bậc hai biến x là hàm số cho bởi công thức dạng $y = f(x) = a{x^2} + bx + c$ $y = f(x) = a{x^2} + bx + c$ với $a,b,c \in \mathbb{R};a \ne 0.$ $a,b,c \in \mathbb{R};a \ne 0.$

+ Tập xác định:R

2. Sự biến thiên của hàm số bậc hai

+) Kết luận:

	a > 0	a < 0
Trên khoảng $\left( { - \infty ;\frac{{ - b}}{{2a}}} \right)$ $\left( { - \infty ;\frac{{ - b}}{{2a}}} \right)$	Hàm số nghịch biến	Hàm số đồng biến
Trên khoảng $\left( {\frac{{ - b}}{{2a}}; + \infty } \right)$ $\left( {\frac{{ - b}}{{2a}}; + \infty } \right)$	Hàm số đồng biến	Hàm số nghịch biến
GTLN hoặc GTNN	Đạt GTNN bằng $\frac{{ - \Delta }}{{4a}}$ $\frac{{ - \Delta }}{{4a}}$ tại $x = \frac{{ - b}}{{2a}}$ $x = \frac{{ - b}}{{2a}}$	Đạt GTLN bằng $\frac{{ - \Delta }}{{4a}}$ $\frac{{ - \Delta }}{{4a}}$ tại $x = \frac{{ - b}}{{2a}}$ $x = \frac{{ - b}}{{2a}}$
Tập giá trị	$T = \left[ {\left. {\frac{{ - \Delta }}{{4a}}; + \infty } \right)} \right.$ $T = \left[ {\left. {\frac{{ - \Delta }}{{4a}}; + \infty } \right)} \right.$