Toán 10 Bài 1: Khái niệm vectơ Giải SGK Toán 10 trang 86 - Tập 1 sách Chân trời sáng tạo
Giải Toán lớp 10 trang 86, 87 tập 1 Chân trời sáng tạo giúp các bạn học sinh có thêm nhiều gợi ý tham khảo để trả lời các câu hỏi Luyện tập và các bài tập trong SGK bài 1 Khái niệm vectơ.
Toán 10 Chân trời sáng tạo tập 1 trang 86, 87 được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa môn Toán lớp 10. Giải Toán lớp 10 trang 86, 87 là tài liệu cực kì hữu ích hỗ trợ các em học sinh trong quá trình giải bài tập. Đồng thời phụ huynh có thể sử dụng để hướng dẫn con em học tập và đổi mới phương pháp giải phù hợp hơn.
Toán 10 Bài 1: Khái niệm vectơ
I. Trả lời câu hỏi Hoạt động Toán 10 Bài 1
Hoạt động 1
Trong thông báo: Có một con tàu chở 500 tấn hàng từ cảng A đến cảng B cách nhau 500 km.
Bạn hãy tìm sự khác biệt giữa hai đại lượng sau:
- Khối lượng của hàng: 500 tấn.
- Độ dịch chuyển của tàu: 500 km từ A đến B.
Gợi ý đáp án
Chỉ ra sự khác biệt như sau:
- Vì hàng trên tàu có khối lượng 500 tấn
=> Khối lượng của hàng là đại lượng chỉ có độ lớn
=> Đây là đại lượng vô hướng
- Vì con tàu có độ dịch chuyển dài 500 km theo hướng từ A đến B.
=> Độ dịch chuyển của tàu là đại lượng bao gồm cả độ lớn và hướng
=> Đây là đại lượng có hướng
Hoạt động 2
Bạn có nhận xét gì về giá của các cặp vectơ ![]() \(\overrightarrow {AB}\) và
\(\overrightarrow {AB}\) và ![]() \(\overrightarrow {CD}\) ,
\(\overrightarrow {CD}\) , ![]() \(\overrightarrow {PQ}\) và
\(\overrightarrow {PQ}\) và ![]() \(\overrightarrow {RS}\) trong Hình 6?
\(\overrightarrow {RS}\) trong Hình 6?
Gợi ý đáp án
Giá của vectơ ![]() \(\overrightarrow {AB}\) là đường thẳng AB, giá của vectơ
\(\overrightarrow {AB}\) là đường thẳng AB, giá của vectơ ![]() \(\overrightarrow {CD}\) là đường thẳng CD.
\(\overrightarrow {CD}\) là đường thẳng CD.
Quan sát Hình 6 ta thấy hai đường thẳng AB, CD là trùng nhau.
=> giá của hai vectơ ![]() \(\overrightarrow {AB}\) và
\(\overrightarrow {AB}\) và ![]() \(\overrightarrow {CD}\) là trùng nhau.
\(\overrightarrow {CD}\) là trùng nhau.
+ Giá của vectơ ![]() \(\overrightarrow {PQ}\) là đường thẳng PQ, giá của vectơ
\(\overrightarrow {PQ}\) là đường thẳng PQ, giá của vectơ ![]() \(\overrightarrow {RS}\) là đường thẳng RS.
\(\overrightarrow {RS}\) là đường thẳng RS.
Quan sát Hình 6 ta thấy hai đường thẳng PQ và RS song song với nhau.
=> Giá của hai vectơ ![]() \(\overrightarrow {PQ}\) và
\(\overrightarrow {PQ}\) và ![]() \(\overrightarrow {RS}\) là song song với nhau.
\(\overrightarrow {RS}\) là song song với nhau.
Hoạt động 3
Cho hình bình hành ABCD (Hình 10), hãy so sánh độ dài và hướng của hai vecto:
Gợi ý đáp án
Ta có: ABCD là hình bình hành
=> AB // DC và AB = DC; AD // CB và AD = CB
a) Hai vectơ ![]() \(\overrightarrow {AB}\) và
\(\overrightarrow {AB}\) và ![]() \(\overrightarrow {DC}\) có giá lần lượt là đường thẳng AB và đường thẳng DC song song với nhau và có cùng hướng đi từ trái sang phải.
\(\overrightarrow {DC}\) có giá lần lượt là đường thẳng AB và đường thẳng DC song song với nhau và có cùng hướng đi từ trái sang phải.
=> Hai vectơ ![]() \(\overrightarrow {AB}\) và
\(\overrightarrow {AB}\) và ![]() \(\overrightarrow {DC}\) cùng hướng
\(\overrightarrow {DC}\) cùng hướng
Mà ![]() \(\overrightarrow {\left| {AB} \right|} = \left| {\overrightarrow {DC} } \right|\) (do AB = CD)
\(\overrightarrow {\left| {AB} \right|} = \left| {\overrightarrow {DC} } \right|\) (do AB = CD)
b) Hai vectơ ![]() \(\overrightarrow {AD}\) và
\(\overrightarrow {AD}\) và ![]() \(\overrightarrow {CB}\) có giá song song với nhau và có hướng ngược nhau
\(\overrightarrow {CB}\) có giá song song với nhau và có hướng ngược nhau
=> Hai vectơ ![]() \(\overrightarrow {AD}\) và
\(\overrightarrow {AD}\) và ![]() \(\overrightarrow {CB}\) ngược hướng
\(\overrightarrow {CB}\) ngược hướng
![]() \(\overrightarrow {\left| {AD} \right|} = \left| {\overrightarrow {BC} } \right|\) (do AD = CB)
\(\overrightarrow {\left| {AD} \right|} = \left| {\overrightarrow {BC} } \right|\) (do AD = CB)
II. Giải Toán 10 trang 86, 87 Chân trời sáng tạo - Tập 1
Bài 1 trang 86
a) Bạn hãy tìm sự khác biệt giữa hai đại lượng sau:
- Bác Ba có số tiền 20 triệu đồng
- Một cơn bão di chuyển với vận tốc 20 km/h theo hướng đông bắc.
b) Trong các đại lượng sau, đại lượng nào cần được biểu diễn bởi vectơ?
Giá tiền, lực, thể tích, tuổi, độ dịch chuyển, vận tốc
Gợi ý đáp án
a) Sự khác biệt là:
- Đơn vị của 2 đại lượng: triệu đồng và km/h
- 20 triệu đồng là 1 đại lượng vô hướng còn cơn bão là đại lượng có hướng cụ thể là hướng từ đông sang bắc với vận tốc là 20 km/h
b) Các đại lượng cần biểu diễn vectơ là các đại lượng có hướng nên đó là: lực, độ dịch chuyển, vận tốc.
Bài 2 trang 86
Cho hình thang ABCD có hai cạnh đáy là AB và DC (hình 15). Điểm M nằm trên đoạn DC.
a) Gọi tên các vectơ cùng hướng với vectơ ![]() \(\overrightarrow {AB}\)
\(\overrightarrow {AB}\)
b) Gọi tên các vectơ ngược hướng với vectơ ![]() \(\overrightarrow {DM}\)
\(\overrightarrow {DM}\)
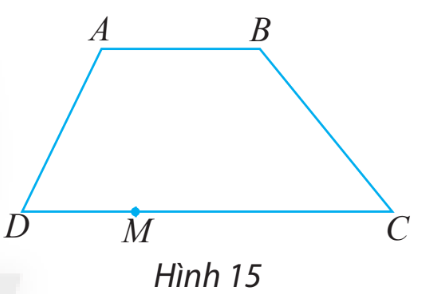
Gợi ý đáp án
a) ABCD là hình thang nên AB//CD
Các vectơ cùng hướng với vectơ ![]() \(\overrightarrow {AB}\) là các vectơ có hướng từ trái qua phải nên đó là:
\(\overrightarrow {AB}\) là các vectơ có hướng từ trái qua phải nên đó là: ![]() \(\overrightarrow {DC} ,\overrightarrow {DM} ,\overrightarrow {MC}\)
\(\overrightarrow {DC} ,\overrightarrow {DM} ,\overrightarrow {MC}\)
b)![]() \(\overrightarrow {DM}\) có hướng từ trái sang phải nên các vectơ ngược hướng với vectơ
\(\overrightarrow {DM}\) có hướng từ trái sang phải nên các vectơ ngược hướng với vectơ ![]() \(\overrightarrow {DM}\) là
\(\overrightarrow {DM}\) là ![]() \(\overrightarrow {BA} ,\overrightarrow {MD} ,\overrightarrow {CM} ,\overrightarrow {CD}\)
\(\overrightarrow {BA} ,\overrightarrow {MD} ,\overrightarrow {CM} ,\overrightarrow {CD}\)
Bài 3 trang 86
Cho hình vuông ABCD có tâm O và có các cạnh bằng a (hình 16)
a) Tìm trong hình hai vectơ bằng nhau và có độ dài bằng ![]() \(\frac{{a\sqrt 2 }}{2}\)
\(\frac{{a\sqrt 2 }}{2}\)
b) Tìm trong hình hai vectơ đối nhau và có độ dài bằng ![]() \(\frac{{a\sqrt 2 }}{2}\)
\(\frac{{a\sqrt 2 }}{2}\)
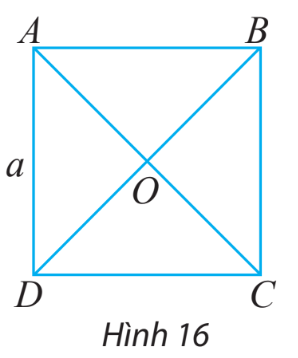
Gợi ý đáp án
![]() \(a) AC = BD = \sqrt {A{D^2} + D{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2\)
\(a) AC = BD = \sqrt {A{D^2} + D{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2\)
![]() \(\Rightarrow AO = OC = BO = OD = \frac{{a\sqrt 2 }}{2}\)
\(\Rightarrow AO = OC = BO = OD = \frac{{a\sqrt 2 }}{2}\)
Suy ra các cặp vectơ bằng nhau và có độ dài bằng ![]() \(\frac{{a\sqrt 2 }}{2}\) là:
\(\frac{{a\sqrt 2 }}{2}\) là:
![]() \(\overrightarrow {AO}\)và
\(\overrightarrow {AO}\)và![]() \(\overrightarrow {AO}\);
\(\overrightarrow {AO}\); ![]() \(\overrightarrow {CO}\)và
\(\overrightarrow {CO}\)và ![]() \(\overrightarrow {OA} ; \overrightarrow {DO}\) và
\(\overrightarrow {OA} ; \overrightarrow {DO}\) và ![]() \(\overrightarrow {OB} ; \overrightarrow {OD} và \overrightarrow {BO}\)
\(\overrightarrow {OB} ; \overrightarrow {OD} và \overrightarrow {BO}\)
b) Các cặp vectơ đối nhau và có độ dài bằng ![]() \(\frac{a\sqrt{2}}{2}\)
\(\frac{a\sqrt{2}}{2}\)
![]() \(\overrightarrow {AO}\) và
\(\overrightarrow {AO}\) và ![]() \(\overrightarrow {CO}\);
\(\overrightarrow {CO}\); ![]() \(\overrightarrow {OA}\)và
\(\overrightarrow {OA}\)và ![]() \(\overrightarrow {OC} ; \overrightarrow {OB}\) và
\(\overrightarrow {OC} ; \overrightarrow {OB}\) và ![]() \(\overrightarrow {OD} ; \overrightarrow {BO}\) và
\(\overrightarrow {OD} ; \overrightarrow {BO}\) và ![]() \(\overrightarrow {DO}\)
\(\overrightarrow {DO}\)
Bài 4 trang 86
Cho tứ giác ABCD. Chứng minh rằng tứ giác đó là hình bình hành khi và chỉ khi ![]() \(\overrightarrow {AB} = \overrightarrow {DC}\)
\(\overrightarrow {AB} = \overrightarrow {DC}\)
Gợi ý đáp án
Tứ giác ABCD là hình bình hành
![]() \(\Leftrightarrow \left\{ \begin{array}{l}
AB // DC\\
AB = DC
\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l}
AB // DC\\
AB = DC
\end{array} \right.\)
Mà ![]() \(AB // DC \Leftrightarrow \overrightarrow {AB} ,\, \overrightarrow {DC}\)cùng phương, do đó cùng hướng.
\(AB // DC \Leftrightarrow \overrightarrow {AB} ,\, \overrightarrow {DC}\)cùng phương, do đó cùng hướng.
 \(\Leftrightarrow \left\{ \begin{array}{l}
\overrightarrow {AB} , \overrightarrow {DC} \,{\rm{ cùng hướng}}\\
AB = DC
\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l}
\overrightarrow {AB} , \overrightarrow {DC} \,{\rm{ cùng hướng}}\\
AB = DC
\end{array} \right.\)
![]() \(\Leftrightarrow \overrightarrow {AB} = \overrightarrow {DC}\)
\(\Leftrightarrow \overrightarrow {AB} = \overrightarrow {DC}\)
Vậy tứ giác ABCD là hình bình hành khi và chỉ khi ![]() \(\overrightarrow {AB} = \overrightarrow {DC} .\)
\(\overrightarrow {AB} = \overrightarrow {DC} .\)
Bài 5 trang 86
Hãy chỉ ra các cặp vectơ cùng hướng, ngược hướng, bằng nhau trong hình 17.
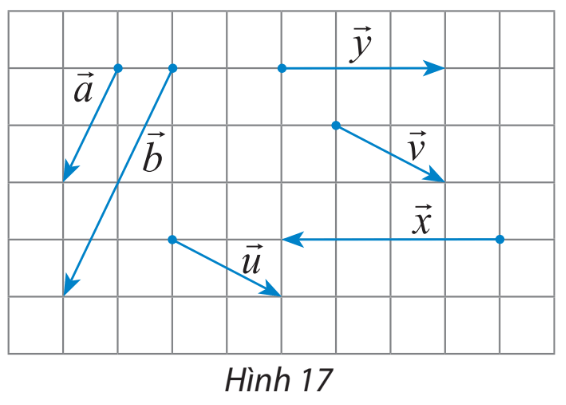
Gợi ý đáp án
+ Các cặp vectơ cùng hướng là: ![]() \(\overrightarrow a và \overrightarrow b ; \overrightarrow u và \overrightarrow v\)
\(\overrightarrow a và \overrightarrow b ; \overrightarrow u và \overrightarrow v\)
+ Các cặp vectơ ngược hướng là:![]() \(\overrightarrow x và \overrightarrow y\)
\(\overrightarrow x và \overrightarrow y\)
+ Các cặp vectơ bằng nhau là: ![]() \(\overrightarrow u và \overrightarrow v\)
\(\overrightarrow u và \overrightarrow v\)
Bài 6 trang 87
Đề bài
Gọi O là tâm hình lục giác đều ABCDEF.
a) Tìm các vectơ khác vectơ ![]() \(\overrightarrow 0\)và cùng hướng với vectơ
\(\overrightarrow 0\)và cùng hướng với vectơ ![]() \(\overrightarrow {OA} .\)
\(\overrightarrow {OA} .\)
b) Tìm các vectơ bằng vectơ ![]() \(\overrightarrow {AB} .\)
\(\overrightarrow {AB} .\)
Gợi ý đáp án
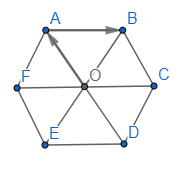
a) Ta có: AO // BC // EF
Suy ra các vectơ khác vectơ khác vectơ ![]() \(\overrightarrow 0\)và cùng hướng với vectơ
\(\overrightarrow 0\)và cùng hướng với vectơ ![]() \(\overrightarrow {OA}\) là :
\(\overrightarrow {OA}\) là : ![]() \(\overrightarrow {DO} ,\overrightarrow {DA} ,\overrightarrow {CB} ,\overrightarrow {EF}\)
\(\overrightarrow {DO} ,\overrightarrow {DA} ,\overrightarrow {CB} ,\overrightarrow {EF}\)
b) Ta có: OA = OB = OC = OD = OE = FO và AB // EC // ED
Suy ra các vectơ bằng vectơ ![]() \(\overrightarrow {AB}\) là
\(\overrightarrow {AB}\) là ![]() \(\overrightarrow {FO} ,\overrightarrow {OC} ,\overrightarrow {ED}\)
\(\overrightarrow {FO} ,\overrightarrow {OC} ,\overrightarrow {ED}\)
Bài 7 trang 87
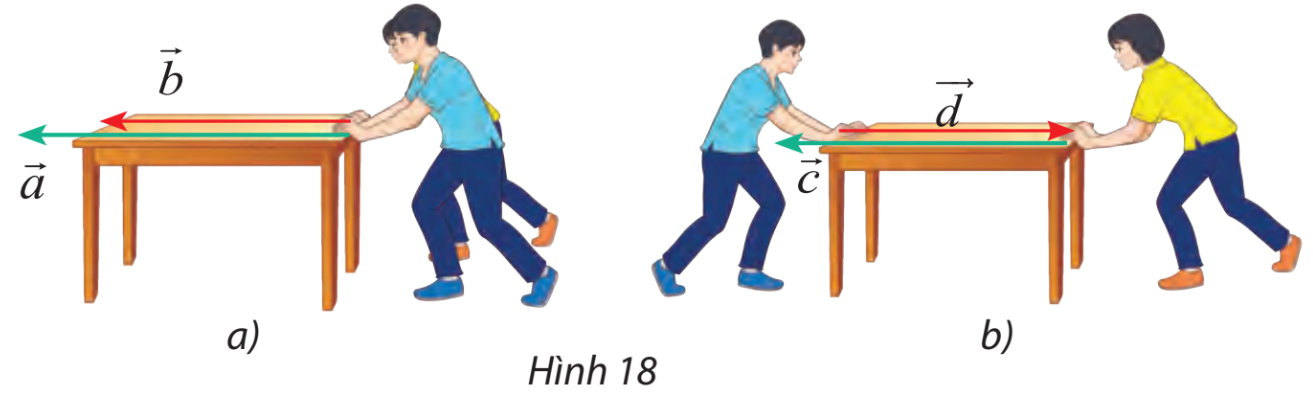
Tìm các lực cùng hướng và ngược hướng trong số các lực đẩy được biểu diễn bằng các vectơ trong hình 18
Gợi ý đáp án
Nhận xét: giá của 4 lực đều song song hoặc trùng nhau, do đó 4 vectơ là cùng phương.
Vectơ ![]() \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c\)có chiều từ phải sang trái còn vectơ
\(\overrightarrow a ,\overrightarrow b ,\overrightarrow c\)có chiều từ phải sang trái còn vectơ ![]() \(\overrightarrow d\)có chiều từ trái sang phải
\(\overrightarrow d\)có chiều từ trái sang phải
Vậy các vectơ (hay lực) cùng hướng với nhau là vectơ ![]() \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c .\)
\(\overrightarrow a ,\overrightarrow b ,\overrightarrow c .\)
Các vectơ (lực) ![]() \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c\)ngược hướng với vectơ
\(\overrightarrow a ,\overrightarrow b ,\overrightarrow c\)ngược hướng với vectơ ![]() \(\overrightarrow d .\)
\(\overrightarrow d .\)
III. Lý thuyết Khái niệm vectơ
1. Khái niệm Vectơ
- Cho đoạn thẳng AB, nếu ta chọn điểm A là điểm đầu, điểm B là điểm cuối thì đoạn thẳng AB có hướng từ A đến B. Khi đó ta nói AB là đoạn thẳng có hướng.
![]() \(\Rightarrow\) Vectơ là đoạn thẳng có hướng.
\(\Rightarrow\) Vectơ là đoạn thẳng có hướng.
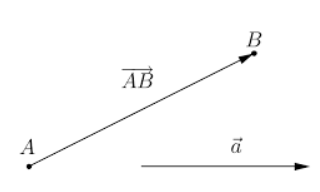
- Khi vectơ có điểm đầu là A và điểm cuối là B, kí hiệu: ![]() \(\overrightarrow{AB}\)
\(\overrightarrow{AB}\)
- Khi vectơ có điểm đầu là B và điểm cuối là A, kí hiệu: ![]() \(\overrightarrow{BA}\)
\(\overrightarrow{BA}\)
- Khi vectơ không có điểm đầu và điểm cuối thì sẽ kí hiệu ![]() \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{m},\overrightarrow{u},....\)
\(\overrightarrow{a},\overrightarrow{b},\overrightarrow{m},\overrightarrow{u},....\)
2. Vectơ cùng phương, vectơ cùng hướng
- Đường thẳng đi qua điểm đầu và điểm cuối của một vectơ được gọi là giá của vectơ.
- Hai vectơ cùng phương nếu giá của chúng song song hoặc trùng nhau.
- Hai vectơ cùng phương có thể cùng hướng hoặc ngược hướng.
Nhận xét: Ba điểm A, B, C thẳng hàng khi và chỉ khi hai vectơ ![]() \(\overrightarrow{AB},\overrightarrow{AC}\) cùng phương.
\(\overrightarrow{AB},\overrightarrow{AC}\) cùng phương.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
Chủ đề liên quan
Có thể bạn quan tâm
-

Văn mẫu lớp 9: Phân tích 2 khổ đầu Viếng lăng Bác của Viễn Phương (Sơ đồ tư duy)
-

Phân tích bài thơ Bàn tay mẹ của Nguyễn Sen
-

Mẫu biên bản sinh hoạt tổ chuyên môn THCS mới
-

Viết bài văn nghị luận về một vấn đề có liên quan đến tuổi trẻ
-

Tập làm văn lớp 4: Đoạn văn miêu tả đặc điểm bên trong chiếc cặp (12 mẫu)
-

Kể về một chuyến tham quan mà em nhớ mãi
-

Toán 6 Bài 22: Hình có tâm đối xứng
-

Văn mẫu lớp 12: Nghị luận về cách vượt qua nghịch cảnh trong cuộc sống
-

Tổng hợp lý thuyết và bài tập Hình học lớp 10 chương 1
-

Suy nghĩ về vai trò của lí tưởng trong cuộc sống con người
Mới nhất trong tuần
-
Toán 10 Bài tập cuối chương X - Chân trời sáng tạo
1.000+ -

Toán 10 Bài 2: Đường thẳng trong mặt phẳng tọa độ
10.000+ -

Toán 10 Bài 1: Dấu của tam thức bậc hai
100+ -

Toán 10 Bài 1: Tọa độ của vectơ
1.000+ -

Toán 10 Bài 2: Hệ bất phương trình bậc nhất hai ẩn
5.000+ -

Toán 10 Bài 2: Định lí Côsin và định lí Sin
10.000+ 2 -

Toán 10 Bài 1: Bất phương trình bậc nhất hai ẩn
1.000+ -

Toán 10 Bài 3: Các phép toán trên tập hợp
5.000+ -

Toán 10 Bài 1: Giá trị lượng giác của một góc từ 0 đến 180
5.000+ -

Toán 10 Bài 2: Tập hợp
10.000+






 Toán 10 Kết nối tri thức
Toán 10 Kết nối tri thức
 Toán 10 Chân trời sáng tạo
Toán 10 Chân trời sáng tạo
 Toán 10 Cánh Diều
Toán 10 Cánh Diều
 Soạn văn 10 Chân trời sáng tạo
Soạn văn 10 Chân trời sáng tạo
 Soạn văn 10 Cánh Diều
Soạn văn 10 Cánh Diều
 Soạn văn 10 Kết nối tri thức
Soạn văn 10 Kết nối tri thức
 Tiếng Anh 10 Global Success
Tiếng Anh 10 Global Success
 Tiếng anh 10 Friends Global
Tiếng anh 10 Friends Global
 Tiếng Anh 10 Explore New Worlds
Tiếng Anh 10 Explore New Worlds