Toán 10 Bài tập cuối chương IX - Chân trời sáng tạo Giải SGK Toán 10 trang 73 - Tập 2

Giới thiệu Tải về Bình luận

Giải Toán 10 Bài tập cuối chương IX giúp các em học sinh lớp 10 tham khảo, biết cách giải các bài tập trong SGK Toán 10 Tập 2 trang 73 sách Chân trời sáng tạo.

Giải SGK Toán 10 Bài tập cuối chương 9 Phương pháp tọa độ trong mặt phẳng sách Chân trời sáng tạo Tập 2 giúp các em học sinh nắm được cách trình bày, cách triển khai để giải được các bài tập từ bài 1 đến bài 9 trong sách giáo khoa. Từ đó các em học sinh tự bồi dưỡng và nâng cao kiến thức tự tin giải quyết tốt các bài tập. Đồng thời đây cũng là tư liệu hữu ích giúp thầy cô tham khảo để soạn giáo án cho riêng mình.

Giải Toán 10 trang 73 Chân trời sáng tạo - Tập 2

Bài 1 trang 73

Trong mặt phẳng Oxy, cho bốn điểm A(2; 1), B(1; 4), C(4; 5), D(5; 2).

a. Chứng minh ABCD là hình vuông.

b. Tìm tọa độ tâm I của hình vuông ABCD.

Gợi ý đáp án

a. Ta có: $\vec{AB} = (-1; 3), \vec{DC} = (-1; 3) \Rightarrow \vec{AB} = \vec{DC}$ $\vec{AB} = (-1; 3), \vec{DC} = (-1; 3) \Rightarrow \vec{AB} = \vec{DC}$

$\Rightarrow$ $\Rightarrow$ ABCD là hình bình hành.

Lại có: $\vec{AD} = (3; 1) \Rightarrow \vec{AB}. \vec{AD} = -1. 3 + 3. 1 = 0$ $\vec{AD} = (3; 1) \Rightarrow \vec{AB}. \vec{AD} = -1. 3 + 3. 1 = 0$

$\Rightarrow \vec{AB} \perp \vec{AD} hay AB \perp AD$ $\Rightarrow \vec{AB} \perp \vec{AD} hay AB \perp AD$

$\Rightarrow$ $\Rightarrow$Hình bình hành ABCD là hình chữ nhật.

Ta có: $AD = |\vec{AD}| = \sqrt{3^{2} + 1^{2}} = \sqrt{10}$ $AD = |\vec{AD}| = \sqrt{3^{2} + 1^{2}} = \sqrt{10}$

$AB = |\vec{AB}| = \sqrt{(-1)^{2} + 3^{2}} = \sqrt{10}$ $AB = |\vec{AB}| = \sqrt{(-1)^{2} + 3^{2}} = \sqrt{10}$

$\Rightarrow AB = AD \Rightarrow$ $\Rightarrow AB = AD \Rightarrow$Hình chữ nhật ABCD là hình vuông (đpcm).

b. Tâm I của hình vuông ABCD là trung điểm của $AC \Rightarrow I = (\frac{2 + 4}{2}; \frac{1+5}{2}) \Leftrightarrow I = (3; 3)$ $AC \Rightarrow I = (\frac{2 + 4}{2}; \frac{1+5}{2}) \Leftrightarrow I = (3; 3)$

Vậy I = (3; 3).

Bài 2 trang 73

Cho AB và CD là dây cung vuông góc tại E của đường tròn (O). Vẽ hình chữ nhật AECF. Dùng phương pháp tọa độ để chứng minh EF vuông góc với DB.

Gợi ý đáp án

Chọn hệ tọa độ Oxy như hình vẽ. A(a; 0), B(b; 0), C(0; c), D(0; d). Hai dây cung AB và CD vuông góc với nhau tại E (trùng với gốc tọa độ O).

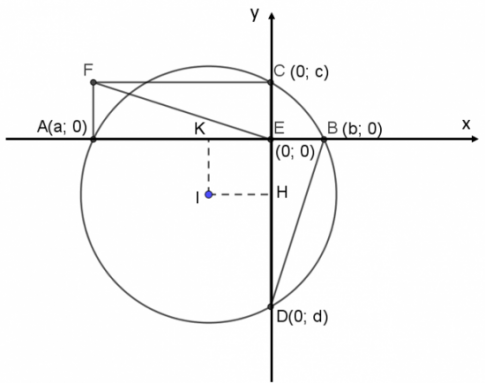
Vì ACEF là hình chữ nhật nên F(a; c).

Gọi I là tâm đường tròn (O), K và H lần lượt là chân đường cao hạ từ I tới AB, CD.

$\Rightarrow K$ $\Rightarrow K$ là trung điểm của $AB \Rightarrow K = (\frac{a + b}{2}; 0)$ $AB \Rightarrow K = (\frac{a + b}{2}; 0)$

H là trung điểm của $CD \Rightarrow H = (0; \frac{c + d}{2})$ $CD \Rightarrow H = (0; \frac{c + d}{2})$

$\Rightarrow I = (\frac{a + b}{2}; \frac{c + d}{2})$ $\Rightarrow I = (\frac{a + b}{2}; \frac{c + d}{2})$

Ta có: $\vec{IA} = (a - \frac{a + b}{2}; -\frac{c + d}{2}) = (\frac{a - b}{2}; -\frac{c + d}{2})$ $\vec{IA} = (a - \frac{a + b}{2}; -\frac{c + d}{2}) = (\frac{a - b}{2}; -\frac{c + d}{2})$

$\vec{IC} = ( -\frac{a + b}{2}; c - \frac{c + d}{2}) = (-\frac{a + b}{2}; \frac{c - d}{2}$ $\vec{IC} = ( -\frac{a + b}{2}; c - \frac{c + d}{2}) = (-\frac{a + b}{2}; \frac{c - d}{2}$

Vì $IA = IC (=R) \Rightarrow (\frac{a - b}{2})^{2} + (-\frac{c + d}{2})^{2} = (-\frac{a + b}{2})^{2} + (\frac{c - d}{2})^{2}$ $IA = IC (=R) \Rightarrow (\frac{a - b}{2})^{2} + (-\frac{c + d}{2})^{2} = (-\frac{a + b}{2})^{2} + (\frac{c - d}{2})^{2}$

$\Leftrightarrow (a - b)^{2} + (c + d)^{2} = (a + b)^{2} + (c - d)^{2}$ $\Leftrightarrow (a - b)^{2} + (c + d)^{2} = (a + b)^{2} + (c - d)^{2}$

$\Leftrightarrow a^{2} - 2ab + b^{2} + c^{2} + 2cd + d^{2} = a^{2} + 2ab + b^{2} + c^{2} - 2cd + d^{2}$ $\Leftrightarrow a^{2} - 2ab + b^{2} + c^{2} + 2cd + d^{2} = a^{2} + 2ab + b^{2} + c^{2} - 2cd + d^{2}$

$\Leftrightarrow 4ab = 4cd \Leftrightarrow ab = cd \Leftrightarrow ab - cd = 0$ $\Leftrightarrow 4ab = 4cd \Leftrightarrow ab = cd \Leftrightarrow ab - cd = 0$

$\Rightarrow \vec{EF}. \vec{BD} = (-a).(-b) - c.d = ab - cd = 0$ $\Rightarrow \vec{EF}. \vec{BD} = (-a).(-b) - c.d = ab - cd = 0$ (chứng minh trên)

$\Rightarrow \vec{EF} \perp \vec{BD} hay EF \perp BD (đpcm).$ $\Rightarrow \vec{EF} \perp \vec{BD} hay EF \perp BD (đpcm).$

Bài 3 trang 73

Tìm tọa độ giao điểm và góc giữa hai đường thẳng $d_{1}$ $d_{1}$ và $d_{2}$ $d_{2}$ trong mỗi trường hợp sau:

a. $d_{1}: x - y + 2 = 0$ $d_{1}: x - y + 2 = 0$ và $d_{2}: x + y + 4 = 0;$ $d_{2}: x + y + 4 = 0;$

b. $d_{1}: \left\{\begin{matrix}x = 1 + t\\y = 3 + 2t \end{matrix}\right.$ $d_{1}: \left\{\begin{matrix}x = 1 + t\\y = 3 + 2t \end{matrix}\right.$ và $d_{2}: x - 3y + 2 = 0;$ $d_{2}: x - 3y + 2 = 0;$

c. $d_{1}: \left\{\begin{matrix}x = 2 - t\\y = 5 + 3t \end{matrix}\right. và d_{2}: \left\{\begin{matrix}x = 1 + 3t$ $d_{1}: \left\{\begin{matrix}x = 2 - t\\y = 5 + 3t \end{matrix}\right. và d_{2}: \left\{\begin{matrix}x = 1 + 3t'\\3 + 1t' \end{matrix}\right.$

Gợi ý đáp án

a. Đường thẳng $d_{1}$ $d_{1}$ và $d_{2}$ $d_{2}$ có vectơ pháp tuyến lần lượt là $\vec{n_{1}} = (1; -1) và \vec{n_{2}} = (1; 1).$ $\vec{n_{1}} = (1; -1) và \vec{n_{2}} = (1; 1).$

Ta có: $\vec{n_{1}}. \vec{n_{2}} = 1. 1 + (-1). 1 = 0 nên \vec{n_{1}} và \vec{n_{2}}$ $\vec{n_{1}}. \vec{n_{2}} = 1. 1 + (-1). 1 = 0 nên \vec{n_{1}} và \vec{n_{2}}$ là hai vectơ vuông góc $\Rightarrow d_{1} \perp d_{2} \Rightarrow (d_{1}, d_{2}) = 90^{\circ}.$ $\Rightarrow d_{1} \perp d_{2} \Rightarrow (d_{1}, d_{2}) = 90^{\circ}.$

Giao điểm M của $d_{1}$ $d_{1}$ và $d_{2}$ $d_{2}$ là nghiệm của hệ phương trình:

$\left\{\begin{matrix}x - y + 2 = 0\\x + y + 4 = 0 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x = -3 \\y = -1\end{matrix}\right.$ $\left\{\begin{matrix}x - y + 2 = 0\\x + y + 4 = 0 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x = -3 \\y = -1\end{matrix}\right.$

Vậy $d_{1}$ $d_{1}$ và $d_{2}$ $d_{2}$vuông góc và cắt nhau tại M(-3; -1).

b. Ta có: $\vec{u_{1}} = (1; 2)$ $\vec{u_{1}} = (1; 2)$ là vectơ chỉ phương của $d_{1} \Rightarrow \vec{n_{1}} = (2; -1)$ $d_{1} \Rightarrow \vec{n_{1}} = (2; -1)$ là vectơ pháp tuyến của $d_{1}.$ $d_{1}.$

Phương trình tổng quát của $d_1$ đi qua điểm A(1; 3) và nhận $\vec{n_{1}} = (2; -1)$ $\vec{n_{1}} = (2; -1)$ làm vectơ pháp tuyến là: $2(x - 1) - (y - 3) = 0 \Leftrightarrow 2x - y + 1 = 0$ $2(x - 1) - (y - 3) = 0 \Leftrightarrow 2x - y + 1 = 0$

Đường thẳng $d_{2}$ $d_{2}$ có vectơ pháp tuyến là $\vec{n_{2}} = (1; -3)$ $\vec{n_{2}} = (1; -3)$

Ta có: $\frac{2}{1} \neq \frac{-1}{-3} \Rightarrow \vec{n_{1}}$ $\frac{2}{1} \neq \frac{-1}{-3} \Rightarrow \vec{n_{1}}$ và $\vec{n_{2}}$ $\vec{n_{2}}$ là hai vectơ không cùng phương.

$\Rightarrow d_{1} và d_{2}$ $\Rightarrow d_{1} và d_{2}$ cắt nhau. Giao điểm M của $d_{1}$ $d_{1}$ và $d_{2}$ $d_{2}$ là nghiệm của hệ phương trình:

$\left\{\begin{matrix}2x - y + 1 = 0\\x - 3y + 2 = 0\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x = \frac{-1}{5}\\y = \frac{3}{5}\end{matrix}\right.$ $\left\{\begin{matrix}2x - y + 1 = 0\\x - 3y + 2 = 0\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x = \frac{-1}{5}\\y = \frac{3}{5}\end{matrix}\right.$

Ta có: $cos(d_{1}, d_{2}) = \frac{|2. 1 + (-1). (-3)|}{\sqrt{2^{2} + (-1)^{2}}.\sqrt{1^{2} + (-3)^{2}}} = \frac{\sqrt{2}}{2} \Rightarrow (d_{1}, d_{2}) = 45^{\circ}$ $cos(d_{1}, d_{2}) = \frac{|2. 1 + (-1). (-3)|}{\sqrt{2^{2} + (-1)^{2}}.\sqrt{1^{2} + (-3)^{2}}} = \frac{\sqrt{2}}{2} \Rightarrow (d_{1}, d_{2}) = 45^{\circ}$

Vậy $d_{1}$ $d_{1}$ cắt $d_{2}$ $d_{2}$ tại điểm $M(\frac{-1}{5}; \frac{3}{5}) và (d_{1}, d_{2}) = 45^{\circ}.$ $M(\frac{-1}{5}; \frac{3}{5}) và (d_{1}, d_{2}) = 45^{\circ}.$

c. Phương trình tổng quát của $d_{1} và d_{2}$ $d_{1} và d_{2}$lần lượt là:

$d_{1}: 3x + y - 11 = 0 và d_{2}: x - 3y + 8 = 0$ $d_{1}: 3x + y - 11 = 0 và d_{2}: x - 3y + 8 = 0$

Ta có: $\vec{n_{1}}. \vec{n_{2}} = 3. 1 + 1. (-3) = 0 \Rightarrow \vec{n_{1}} \perp \vec{n_{2}} hay d_{1} \perp d_{2} \Rightarrow (d_{1}, d_{2}) = 90^{\circ}.$ $\vec{n_{1}}. \vec{n_{2}} = 3. 1 + 1. (-3) = 0 \Rightarrow \vec{n_{1}} \perp \vec{n_{2}} hay d_{1} \perp d_{2} \Rightarrow (d_{1}, d_{2}) = 90^{\circ}.$

Giao điểm M của đường thẳng $d_{1}$ $d_{1}$ và $d_{2}$ $d_{2}$ là nghiệm của hệ phương trình:

$\left\{\begin{matrix}3x + y - 11 = 0\\x - 3y + 8 = 0\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x = \frac{5}{2}\\y = \frac{7}{2}\end{matrix}\right.$ $\left\{\begin{matrix}3x + y - 11 = 0\\x - 3y + 8 = 0\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x = \frac{5}{2}\\y = \frac{7}{2}\end{matrix}\right.$

Vậy $d_{1}$ $d_{1}$ và $d_{2}$ $d_{2}$vuông góc và cắt nhau tại $M(\frac{5}{2}; \frac{7}{2}).$ $M(\frac{5}{2}; \frac{7}{2}).$

Bài 4 trang 73

Tính bán kính của đường tròn tâm M(-2; 3) và tiếp xúc với đường thẳng:

Gợi ý đáp án

d: 14x - 5y + 60 = 0

Ta có: $R = d(M; d) = \frac{|14. (-2) - 5. 3 + 60|}{\sqrt{14^{2} + (-5)^{2}}} = \frac{\sqrt{221}}{13}$ $R = d(M; d) = \frac{|14. (-2) - 5. 3 + 60|}{\sqrt{14^{2} + (-5)^{2}}} = \frac{\sqrt{221}}{13}$

Bài 5 trang 73

Tính khoảng cách giữa hai đường thẳng:

$\Delta$ $\Delta': 3x + 4y - 27 = 0$

Gợi ý đáp án

Ta có: $\frac{6}{3} = \frac{8}{4} \neq \frac{-13}{-27} \Rightarrow \Delta // \Delta$ $\frac{6}{3} = \frac{8}{4} \neq \frac{-13}{-27} \Rightarrow \Delta // \Delta'$

Lấy điểm $A(0; \frac{13}{8}) \in \Delta.$ $A(0; \frac{13}{8}) \in \Delta.$

Ta có: $d(\Delta, \Delta$ $d(\Delta, \Delta') = d(A; \Delta') = \frac{|4.\frac{13}{8}-27|}{\sqrt{3^{2} + 4^{2}}} = \frac{41}{10}$

Bài 6 trang 73

Tìm tâm và bán kính của các đường tròn có phương trình:

$a. (x - 2)^{2} + (y - 7)^{2} = 64;$ $a. (x - 2)^{2} + (y - 7)^{2} = 64;$

$b. (x + 3)^{2} + (y + 2)^{2} = 8;$ $b. (x + 3)^{2} + (y + 2)^{2} = 8;$

$c. x^{2} + y^{2} - 4x - 6y - 12 = 0.$ $c. x^{2} + y^{2} - 4x - 6y - 12 = 0.$

Gợi ý đáp án

a. Phương trình đường tròn có dạng $(x - a)^{2} + (y - b)^{2} = R^{2}$ $(x - a)^{2} + (y - b)^{2} = R^{2}$

$\Rightarrow$ $\Rightarrow$ Đường tròn có tâm I(2; 7) và bán kính R = 8.

b. Phương trình đường tròn có dạng ( $x - a)^{2} + (y - b)^{2} = R^{2}$ $x - a)^{2} + (y - b)^{2} = R^{2}$

$\Rightarrow$ $\Rightarrow$ Đường tròn có tâm I(-3; -2) và bán kính $R = 2\sqrt{2}.$ $R = 2\sqrt{2}.$

c. Phương trình có dạng $x^{2} + y^{2} - 2ax - 2by + c = 0 với a = 2, b = 3, c = -12$ $x^{2} + y^{2} - 2ax - 2by + c = 0 với a = 2, b = 3, c = -12$

Ta có: $a^{2} + b^{2} - c = 2^{2} + 3^{2} + 12 = 25$ $a^{2} + b^{2} - c = 2^{2} + 3^{2} + 12 = 25$

Vậy đường tròn có tâm I(2; 3) và bán kính $R = \sqrt{25} = 5.$ $R = \sqrt{25} = 5.$

Bài 7 trang 73

Lập phương trình đường tròn trong các trường hợp sau:

a. Có tâm I(-2; 4) và bán kính bằng 9;

b. Có tâm I(1; 2) và đi qua điểm A(4; 5);

c. Đi qua hai điểm A(4; 1), B(6; 5) và có tâm nằm trên đường thẳng 4x + y -16 = 0;

d. Đi qua gốc tọa độ và cắt hai trục tọa độ tại các điểm có hoành độ là a, tung độ là b.

Gợi ý đáp án

a. Phương trình đường tròn có tâm I(-2; 4) và bán kính R = 4 là:

$(x + 2)^{2} + (y - 4)^{2} = 16$ $(x + 2)^{2} + (y - 4)^{2} = 16$

b. Ta có $R = IA = \sqrt{(4 - 1)^{2} + (5 - 2)^{2}} = 3\sqrt{2}$ $R = IA = \sqrt{(4 - 1)^{2} + (5 - 2)^{2}} = 3\sqrt{2}$

Phương trình đường tròn có tâm I(1; 2) và bán kính $R = 3\sqrt{2}$ $R = 3\sqrt{2}$ là:

$(x - 1)^{2} + (y - 2)^{2} = 18$ $(x - 1)^{2} + (y - 2)^{2} = 18$

c. Phương trình đường tròn tâm I(a; b) có dạng: $x^{2} + y^{2} - 2ax - 2by + c = 0$ $x^{2} + y^{2} - 2ax - 2by + c = 0$

Vì I(a; b) thuộc đường thẳng 4x + y - 16 = 0 và các điểm A(4; 1), B(6; 5) thuộc đường tròn nên ta có hệ phương trình sau:

$\left\{\begin{matrix}4a + b - 16 = 0\\4^{2} + 1^{2} - 8a-2b +c = 0\\ 6^{2} + 5^{2} - 12a - 10b + c = 0\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}4a + b - 16 = 0\\ 8a+2b -c = 17\\ 12a + 10b - c = 61\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}a = 3\\b = 4 \\ c = 15\end{matrix}\right.$ $\left\{\begin{matrix}4a + b - 16 = 0\\4^{2} + 1^{2} - 8a-2b +c = 0\\ 6^{2} + 5^{2} - 12a - 10b + c = 0\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}4a + b - 16 = 0\\ 8a+2b -c = 17\\ 12a + 10b - c = 61\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}a = 3\\b = 4 \\ c = 15\end{matrix}\right.$

Vậy phương trình đường tròn là: $x^{2} + y^{2} - 6x - 8y + 15 = 0$ $x^{2} + y^{2} - 6x - 8y + 15 = 0$

d. Phương trình đường tròn (C) tâm I(m; n) có dạng: $x^{2} + y^{2} - 2mx - 2ny + c = 0$ $x^{2} + y^{2} - 2mx - 2ny + c = 0$

Vì O(0;0) \in (C) nên thay tọa độ O(0; 0) vào (C) ta được c = 0

Vì (C) cắt trục hoành tại điểm có tọa độ (a; 0) và cắt trục tung tại điểm có tọa độ (0; b) nên ta có:

$\left\{\begin{matrix}a^{2} - 2ma = 0\\b^{2} - 2nb = 0\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} m = \frac{a}{2}\\n = \frac{b}{2}\end{matrix}\right. (vì a \neq 0, b\neq 0)$ $\left\{\begin{matrix}a^{2} - 2ma = 0\\b^{2} - 2nb = 0\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} m = \frac{a}{2}\\n = \frac{b}{2}\end{matrix}\right. (vì a \neq 0, b\neq 0)$

Vậy phương trình đường tròn (C) là: $x^{2} + y^{2} - ax - by = 0$ $x^{2} + y^{2} - ax - by = 0$

Bài 8 trang 73

Viết phương trình tiếp tuyến của đường tròn (C): $(x - 5)^{2} + (y - 3)^{2} = 100$ $(x - 5)^{2} + (y - 3)^{2} = 100$ tại điểm M(11; 11)

Gợi ý đáp án

Ta có: (C) có tâm I(5; 3).

Phương trình tiếp tuyến của đường tròn (C) tại M(11; 11) là:

$(5 - 11)(x - 11) + (3 - 11)(y - 11) = 0$

$\Leftrightarrow -6x - 8y + 154 = 0$ $\Leftrightarrow -6x - 8y + 154 = 0$

$\Leftrightarrow 3x + 4y - 77 = 0$ $\Leftrightarrow 3x + 4y - 77 = 0$

Bài 9 trang 73

Tìm tọa độ các tiêu điểm, tọa độ các đỉnh, độ dài trục lớn và trục nhỏ của các elip sau:

$a. \frac{x^{2}}{100} + \frac{y^{2}}{36} = 1;$ $a. \frac{x^{2}}{100} + \frac{y^{2}}{36} = 1;$

$b. \frac{x^{2}}{25} + \frac{y^{2}}{16} = 1;$ $b. \frac{x^{2}}{25} + \frac{y^{2}}{16} = 1;$

$c. x^{2} + 16y^{2} = 16$ $c. x^{2} + 16y^{2} = 16$

Gợi ý đáp án

$a. (E): \frac{x^{2}}{100} + \frac{y^{2}}{36} = 1$ $a. (E): \frac{x^{2}}{100} + \frac{y^{2}}{36} = 1$

Phương trình elip (E) có dạng: $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$

$\Rightarrow a = 10; b = 6 \Rightarrow c = \sqrt{a^{2} - b^{2}} = \sqrt{10^{2} - 6^{2}} = 8$ $\Rightarrow a = 10; b = 6 \Rightarrow c = \sqrt{a^{2} - b^{2}} = \sqrt{10^{2} - 6^{2}} = 8$

$\Rightarrow$ $\Rightarrow$ Tọa độ các tiêu điểm là: (-8; 0) và (8; 0)

Tọa độ các đỉnh là: (-10; 0), (10; 0), (0; -6); (0; 6)

Độ dài trục lớn bằng 2a = 2. 10 = 20; độ dài trục nhỏ bằng 2b = 2. 6 = 12.

$b. (E): \frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$ $b. (E): \frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$

Phương trình elip (E) có dạng: $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$

$\Rightarrow a = 5; b = 4 \Rightarrow c = \sqrt{a^{2} - b^{2}} = \sqrt{5^{2} - 4^{2}} = 3$ $\Rightarrow a = 5; b = 4 \Rightarrow c = \sqrt{a^{2} - b^{2}} = \sqrt{5^{2} - 4^{2}} = 3$

$\Rightarrow$ $\Rightarrow$Tọa độ các tiêu điểm là: (-3; 0) và (3; 0)

Tọa độ các đỉnh là: (-5; 0), (5; 0), (0; -4); (0; 4)

Độ dài trục lớn bằng 2a = 2. 5 = 10; độ dài trục nhỏ bằng 2b = 2. 4 = 8.

c. Ta có: $x^{2} + 16y^{2} = 16 \Leftrightarrow \frac{x^{2}}{16} + y^{2} = 1$ $x^{2} + 16y^{2} = 16 \Leftrightarrow \frac{x^{2}}{16} + y^{2} = 1$

Phương trình elip (E) có dạng: $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$

$\Rightarrow a = 4; b = 1 \Rightarrow c = \sqrt{a^{2} - b^{2}} = \sqrt{4^{2} - 1^{2}} = \sqrt{15}$ $\Rightarrow a = 4; b = 1 \Rightarrow c = \sqrt{a^{2} - b^{2}} = \sqrt{4^{2} - 1^{2}} = \sqrt{15}$

$\Rightarrow$ $\Rightarrow$ Tọa độ các tiêu điểm là: $(-\sqrt{15}; 0) và (\sqrt{15}; 0)$ $(-\sqrt{15}; 0) và (\sqrt{15}; 0)$

Tọa độ các đỉnh là: (-4; 0), (4; 0), (0; -1); (0; 1)

Độ dài trục lớn bằng 2a = 2. 4 = 8; độ dài trục nhỏ bằng 2b = 2. 1 = 2.

Chia sẻ bởi: