Toán 10 Bài tập cuối chương IV - Chân trời sáng tạo Giải SGK Toán 10 trang 78 - Tập 1

Tải về Bình luận

Bài trước

Mục lục

Bài sau

Toán 10 Chân trời sáng tạo trang 78, 79 giúp các bạn học sinh có thêm nhiều gợi ý tham khảo để trả lời 10 bài tập trong SGK Toán 10 tập 1.

Bài tập cuối chương 4 Toán 10 Chân trời sáng tạo được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa. Giải Toán 10 Bài tập cuối chương IV trang 78, 79 là tài liệu cực kì hữu ích hỗ trợ các em học sinh lớp 10 trong quá trình giải bài tập. Đồng thời phụ huynh có thể sử dụng để hướng dẫn con em học tập và đổi mới phương pháp giải phù hợp hơn.

Bài tập cuối chương 4 Toán 10 Chân trời sáng tạo

Giải Toán 10 trang 78, 79 Chân trời sáng tạo - Tập 1

Giải Toán 10 trang 78, 79 Chân trời sáng tạo - Tập 1

Bài 1 trang 78

Cho tam giác ABC. Biết a = 49,4;b = 26,4 $;\widehat C = {47^ \circ }20$ $;\widehat C = {47^ \circ }20'.$ Tính hai góc $\widehat A,\widehat B$ $\widehat A,\widehat B$và cạnh c.

Hướng dẫn giải

- Giải tam giác là tìm số đo các cạnh và các góc còn lại của tam giác khi ta biết các yếu tố đủ để xác định tam giác đó.

- Định lí cosin:

a² = b² + c² – 2bc.cosA

b² = a² + c² – 2ac.cosB

c² = a² + b² – 2ab.cosC

Trong tam giác ABC có: $\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R$ $\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R$

Học sinh xem lại các công thức tính diện tích tam giác đã được học.

Gợi ý đáp án

Áp dụng định lí cosin trong tam giác ABC, ta có:

$\begin{array}{l}{c^2} = {b^2} + {a^2} - 2ab\cos C\\ \Leftrightarrow {c^2} = 26,{4^2} + 49,{4^2} - 2.26,4.49,4\cos {47^ \circ }20$ $\begin{array}{l}{c^2} = {b^2} + {a^2} - 2ab\cos C\\ \Leftrightarrow {c^2} = 26,{4^2} + 49,{4^2} - 2.26,4.49,4\cos {47^ \circ }20'\\ \Rightarrow c \approx 37\end{array}$

Áp dụng định lí sin, ta có: $\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}}$ $\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}}$

$\begin{array}{l} \Leftrightarrow \frac{{49,4}}{{\sin A}} = \frac{{26,4}}{{\sin B}} = \frac{{37}}{{\sin {{47}^ \circ }20$ $\begin{array}{l} \Leftrightarrow \frac{{49,4}}{{\sin A}} = \frac{{26,4}}{{\sin B}} = \frac{{37}}{{\sin {{47}^ \circ }20'}}\\ \Rightarrow \sin A = \frac{{49,4.\sin {{47}^ \circ }20'}}{{37}} \approx 0,982 \Rightarrow \widehat A \approx {79^ \circ }\\ \Rightarrow \widehat B \approx {180^ \circ } - {79^ \circ } - {47^ \circ }20' = {53^ \circ }40'\end{array}$

Bài 2 trang 78

Cho tam giác ABC. Biết a = 24,b = 13,c = 15. Tính các góc $\widehat A,\widehat B,\widehat C.$ $\widehat A,\widehat B,\widehat C.$

Gợi ý đáp án

Áp dụng hệ quả của định lí cosin, ta có:

$\begin{array}{l}\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\\ \Rightarrow \cos A = \frac{{{{13}^2} + {{15}^2} - {{24}^2}}}{{2.13.15}} = - \frac{7}{{15}};\cos B = \frac{{{{24}^2} + {{15}^2} - {{13}^2}}}{{2.24.15}} = \frac{{79}}{{90}}\\ \Rightarrow \widehat A \approx 117,{8^ \circ },\widehat B \approx 28,{6^o}\\ \Rightarrow \widehat C \approx 33,{6^o}\end{array}$ $\begin{array}{l}\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\\ \Rightarrow \cos A = \frac{{{{13}^2} + {{15}^2} - {{24}^2}}}{{2.13.15}} = - \frac{7}{{15}};\cos B = \frac{{{{24}^2} + {{15}^2} - {{13}^2}}}{{2.24.15}} = \frac{{79}}{{90}}\\ \Rightarrow \widehat A \approx 117,{8^ \circ },\widehat B \approx 28,{6^o}\\ \Rightarrow \widehat C \approx 33,{6^o}\end{array}$

Bài 3 trang 78

Cho tam giác ABC có a = 8,b = 10,c = 13. Tính các góc A, B, C

Lựa chọn câu để xem lời giải nhanh hơn

Cho tam giác ABC có a = 8,b = 10,c = 13. Tính các góc $\widehat A,\widehat B,\widehat C.$ $\widehat A,\widehat B,\widehat C.$

Gợi ý đáp án

a) Tam giác ABC có góc tù không?

Áp dụng hệ quả của định lí cosin, ta có:

$\begin{array}{l}\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\\ \Rightarrow \left\{ \begin{array}{l}\cos A = \frac{{{{10}^2} + {{13}^2} - {8^2}}}{{2.10.13}} = \frac{{41}}{{52}} > 0;\\\cos B = \frac{{{8^2} + {{13}^2} - {{10}^2}}}{{2.8.13}} = \frac{{133}}{{208}} > 0\\\cos C = \frac{{{8^2} + {{10}^2} - {{13}^2}}}{{2.8.13}} = - \frac{1}{{32}} < 0\end{array} \right.\end{array}$ $\begin{array}{l}\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\\ \Rightarrow \left\{ \begin{array}{l}\cos A = \frac{{{{10}^2} + {{13}^2} - {8^2}}}{{2.10.13}} = \frac{{41}}{{52}} > 0;\\\cos B = \frac{{{8^2} + {{13}^2} - {{10}^2}}}{{2.8.13}} = \frac{{133}}{{208}} > 0\\\cos C = \frac{{{8^2} + {{10}^2} - {{13}^2}}}{{2.8.13}} = - \frac{1}{{32}} < 0\end{array} \right.\end{array}$

$\Rightarrow \widehat C \approx 91,{79^ \circ } > {90^ \circ }$ $\Rightarrow \widehat C \approx 91,{79^ \circ } > {90^ \circ }$, tam giác ABC có góc C tù.

b) Tính độ dài trung tuyến AM, diện tích tam giác và bán kính đường tròn ngoại tiếp tam giác đó.

Gợi ý đáp án:

+) Áp dụng định lí cosin trong tam giác ACM, ta có:

$\begin{array}{l}A{M^2} = A{C^2} + C{M^2} - 2.AC.CM.\cos C\\ \Leftrightarrow A{M^2} = {8^2} + {5^2} - 2.8.5.\left( { - \frac{1}{{32}}} \right) = 91,5\\ \Rightarrow AM \approx 9,57\end{array}$ $\begin{array}{l}A{M^2} = A{C^2} + C{M^2} - 2.AC.CM.\cos C\\ \Leftrightarrow A{M^2} = {8^2} + {5^2} - 2.8.5.\left( { - \frac{1}{{32}}} \right) = 91,5\\ \Rightarrow AM \approx 9,57\end{array}$

+) Ta có: $p = \frac{{8 + 10 + 13}}{2} = 15,5.$ $p = \frac{{8 + 10 + 13}}{2} = 15,5.$

Áp dụng công thức heron, ta có:

$S = \sqrt {p(p - a)(p - b)(p - c)} = \sqrt {15,5.(15,5 - 8).(15,5 - 10).(15,5 - 13)} \approx 40$ $S = \sqrt {p(p - a)(p - b)(p - c)} = \sqrt {15,5.(15,5 - 8).(15,5 - 10).(15,5 - 13)} \approx 40$

+) Áp dụng định lí sin, ta có:

$\frac{c}{{\sin C}} = 2R \Rightarrow R = \frac{c}{{2\sin C}} = \frac{{13}}{{2.\sin 91,{{79}^ \circ }}} \approx 6,5$ $\frac{c}{{\sin C}} = 2R \Rightarrow R = \frac{c}{{2\sin C}} = \frac{{13}}{{2.\sin 91,{{79}^ \circ }}} \approx 6,5$

c) Lấy điểm D đối xứng với A qua C.

Ta có: $\widehat {BCD} = {180^ \circ } - 91,{79^ \circ } = 88,{21^ \circ }; CD = AC = 8$ $\widehat {BCD} = {180^ \circ } - 91,{79^ \circ } = 88,{21^ \circ }; CD = AC = 8$

Áp dụng định lí cosin trong tam giác BCD, ta có:

$\begin{array}{l}B{D^2} = C{D^2} + C{B^2} - 2.CD.CB.\cos \widehat {BCD}\\ \Leftrightarrow B{D^2} = {8^2} + {10^2} - 2.8.10.\cos 88,{21^ \circ } \approx 159\\ \Rightarrow BD \approx 12,6\end{array}$ $\begin{array}{l}B{D^2} = C{D^2} + C{B^2} - 2.CD.CB.\cos \widehat {BCD}\\ \Leftrightarrow B{D^2} = {8^2} + {10^2} - 2.8.10.\cos 88,{21^ \circ } \approx 159\\ \Rightarrow BD \approx 12,6\end{array}$

Bài 4 trang 79

Cho tam giác ABC có A = 120,b = 8,c = 5. Tính:

a) Cạnh a và các góc B, C

b) Diện tích tam giác ABC

c) Bán kính đường tròn ngoại tiếp và đường cao AH của tam giác.

Gợi ý đáp án

a) Cạnh a và các góc $\widehat B,\widehat C.$ $\widehat B,\widehat C.$

Gợi ý đáp án:

Áp dụng định lí cosin, ta có:

$\begin{array}{l}{a^2} = {b^2} + {c^2} - 2bc.\cos A\\ \Leftrightarrow {a^2} = {8^2} + {5^2} - 2.8.5.\cos {120^ \circ } = 129\\ \Rightarrow a = \sqrt {129} \end{array}$ $\begin{array}{l}{a^2} = {b^2} + {c^2} - 2bc.\cos A\\ \Leftrightarrow {a^2} = {8^2} + {5^2} - 2.8.5.\cos {120^ \circ } = 129\\ \Rightarrow a = \sqrt {129} \end{array}$

Áp dụng định lí sin, ta có:

$\begin{array}{l}\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} \Rightarrow \frac{{\sqrt {129} }}{{\sin {{120}^ \circ }}} = \frac{8}{{\sin B}} = \frac{5}{{\sin C}}\\ \Rightarrow \left\{ \begin{array}{l}\sin B = \frac{{8.\sin {{120}^ \circ }}}{{\sqrt {129} }} \approx 0,61\\\sin C = \frac{{5.\sin {{120}^ \circ }}}{{\sqrt {129} }} \approx 0,38\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\widehat B \approx 37,{59^ \circ }\\\widehat C \approx 22,{41^ \circ }\end{array} \right.\end{array}$ $\begin{array}{l}\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} \Rightarrow \frac{{\sqrt {129} }}{{\sin {{120}^ \circ }}} = \frac{8}{{\sin B}} = \frac{5}{{\sin C}}\\ \Rightarrow \left\{ \begin{array}{l}\sin B = \frac{{8.\sin {{120}^ \circ }}}{{\sqrt {129} }} \approx 0,61\\\sin C = \frac{{5.\sin {{120}^ \circ }}}{{\sqrt {129} }} \approx 0,38\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\widehat B \approx 37,{59^ \circ }\\\widehat C \approx 22,{41^ \circ }\end{array} \right.\end{array}$

b) Diện tích tam giác ABC

Diện tích tam giác ABC là:

$S = \frac{1}{2}bc.\sin A = \frac{1}{2}.8.5.\sin {120^ \circ } = 10\sqrt 3$ $S = \frac{1}{2}bc.\sin A = \frac{1}{2}.8.5.\sin {120^ \circ } = 10\sqrt 3$

c) Bán kính đường tròn ngoại tiếp và đường cao AH của tam giác.

Phương pháp giải:

+) Áp dụng định lí sin: $R = \frac{a}{{\sin A}}$ $R = \frac{a}{{\sin A}}$

+) Đường cao AH: $AH = \frac{{2S}}{a}$ $AH = \frac{{2S}}{a}$

+) Theo định lí sin, ta có: $R = \frac{a}{{\sin A}} = \frac{{\sqrt {129} }}{{\sin {{120}^ \circ }}} = 2\sqrt {43}$ $R = \frac{a}{{\sin A}} = \frac{{\sqrt {129} }}{{\sin {{120}^ \circ }}} = 2\sqrt {43}$

+) Đường cao AH của tam giác bằng: $AH = \frac{{2S}}{a} = \frac{{2.10\sqrt 3 }}{{\sqrt {129} }} = \frac{{20\sqrt {43} }}{{43}}$ $AH = \frac{{2S}}{a} = \frac{{2.10\sqrt 3 }}{{\sqrt {129} }} = \frac{{20\sqrt {43} }}{{43}}$

Bài 5 trang 79

Cho hình bình hành ABCD

a) Chứng minh $2\left( {A{B^2} + B{C^2}} \right) = A{C^2} + B{D^2}$ $2\left( {A{B^2} + B{C^2}} \right) = A{C^2} + B{D^2}$

b) Cho AB = 4,BC = 5,BD = 7. Tính AC.

Gợi ý đáp án

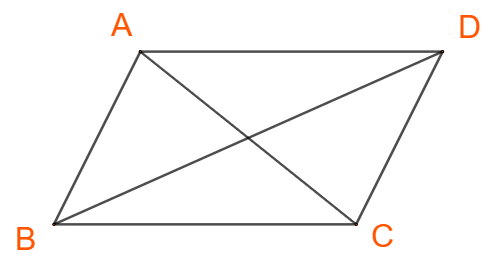
a) Áp dụng định lí cosin ta có

$\left\{ \begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\\B{D^2} = A{B^2} + A{D^2} - 2.AB.AD.\cos A\end{array} \right.$ $\left\{ \begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\\B{D^2} = A{B^2} + A{D^2} - 2.AB.AD.\cos A\end{array} \right.$

Mà $AD = BC;\cos A = \cos ({180^ \circ } - B) = - \cos B$ $AD = BC;\cos A = \cos ({180^ \circ } - B) = - \cos B$

$\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}A{C^2} = A{B^2} + B{C^2} + 2.AB.BC.\cos A\\B{D^2} = A{B^2} + B{C^2} - 2.AB.AD.\cos A\end{array} \right.\\ \Rightarrow A{C^2} + B{D^2} = 2\left( {A{B^2} + B{C^2}} \right)\end{array}$ $\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}A{C^2} = A{B^2} + B{C^2} + 2.AB.BC.\cos A\\B{D^2} = A{B^2} + B{C^2} - 2.AB.AD.\cos A\end{array} \right.\\ \Rightarrow A{C^2} + B{D^2} = 2\left( {A{B^2} + B{C^2}} \right)\end{array}$

b) Theo câu a, ta suy ra: $A{C^2} = 2\left( {A{B^2} + B{C^2}} \right) - B{D^2}$ $A{C^2} = 2\left( {A{B^2} + B{C^2}} \right) - B{D^2}$

$\begin{array}{l} \Rightarrow A{C^2} = 2\left( {{4^2} + {5^2}} \right) - {7^2} = 33\\ \Rightarrow AC = \sqrt {33} \end{array}$ $\begin{array}{l} \Rightarrow A{C^2} = 2\left( {{4^2} + {5^2}} \right) - {7^2} = 33\\ \Rightarrow AC = \sqrt {33} \end{array}$

Bài 6 trang 79

Cho tam giác ABC có a = 15,b = 20,c = 25.

a) Tính diện tích tam giác ABC

b) Tính bán kính đường tròn ngoại tiếp tam giác ABC

Gợi ý đáp án

a) Ta có: $p = \frac{{a + b + c}}{2} = \frac{{15 + 20 + 25}}{2} = 30$ $p = \frac{{a + b + c}}{2} = \frac{{15 + 20 + 25}}{2} = 30$

Áp dụng công thức heron, ta có: $S = \sqrt {30.(30 - 15).(30 - 20).(30 - 25)} = 150$ $S = \sqrt {30.(30 - 15).(30 - 20).(30 - 25)} = 150$

b) Ta có: $S = \frac{{abc}}{{4R}} \Rightarrow R = \frac{{abc}}{{4S}} = \frac{{15.20.25}}{{4.150}} = 12,5.$ $S = \frac{{abc}}{{4R}} \Rightarrow R = \frac{{abc}}{{4S}} = \frac{{15.20.25}}{{4.150}} = 12,5.$

Bài 7 trang 79

Cho tam giác ABC. Chứng minh rằng:

$\cot A + \cot B + \cot C = \frac{{R({a^2} + {b^2} + {c^2})}}{{abc}}$ $\cot A + \cot B + \cot C = \frac{{R({a^2} + {b^2} + {c^2})}}{{abc}}$

Gợi ý đáp án

Áp dụng hệ quả của định lí sin và định lí cosin, ta có:

$\frac{a}{{\sin A}} = 2R \Rightarrow \sin A = \frac{a}{{2R}}$ $\frac{a}{{\sin A}} = 2R \Rightarrow \sin A = \frac{a}{{2R}}$

và $\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}$ $\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}$

$\Rightarrow \cot A = \frac{{\cos A}}{{\sin A}} = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}:\frac{a}{{2R}} = R.\frac{{{b^2} + {c^2} - {a^2}}}{{abc}}$ $\Rightarrow \cot A = \frac{{\cos A}}{{\sin A}} = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}:\frac{a}{{2R}} = R.\frac{{{b^2} + {c^2} - {a^2}}}{{abc}}$

Tương tự ta có: $\cot B = R.\frac{{{a^2} + {c^2} - {b^2}}}{{abc}} và \cot C = R.\frac{{{a^2} + {b^2} - {c^2}}}{{abc}}$ $\cot B = R.\frac{{{a^2} + {c^2} - {b^2}}}{{abc}} và \cot C = R.\frac{{{a^2} + {b^2} - {c^2}}}{{abc}}$

$\begin{array}{l} \Rightarrow \cot A + \cot B + \cot C = \frac{R}{{abc}}\left[ {\left( {{b^2} + {c^2} - {a^2}} \right) + \left( {{a^2} + {c^2} - {b^2}} \right) + \left( {{a^2} + {b^2} - {c^2}} \right)} \right]\\ = \frac{R}{{abc}}\left( {2{b^2} + 2{c^2} + 2{a^2} - {a^2} - {c^2} - {b^2}} \right) = \frac{{R({a^2} + {b^2} + {c^2})}}{{abc}}\end{array}$ $\begin{array}{l} \Rightarrow \cot A + \cot B + \cot C = \frac{R}{{abc}}\left[ {\left( {{b^2} + {c^2} - {a^2}} \right) + \left( {{a^2} + {c^2} - {b^2}} \right) + \left( {{a^2} + {b^2} - {c^2}} \right)} \right]\\ = \frac{R}{{abc}}\left( {2{b^2} + 2{c^2} + 2{a^2} - {a^2} - {c^2} - {b^2}} \right) = \frac{{R({a^2} + {b^2} + {c^2})}}{{abc}}\end{array}$

Bài 8 trang 79

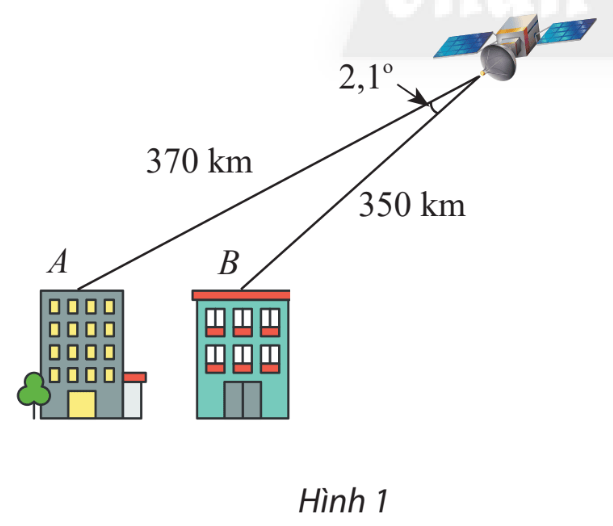
Tính khoảng cách AB giữa hai nóc tòa cao ốc. Cho biết khoảng cách từ hai điểm đó đến một vệ tinh viễn thông lần lượt là 370 km, 350 km và góc nhìn từ vệ tinh đến A và B là $2,{1^ \circ }.$ $2,{1^ \circ }.$

Gợi ý đáp án

Áp dụng định lí cosin, ta có:

$\begin{array}{l}A{B^2} = {370^2} + {350^2} - 2.370.350.\cos 2,{1^ \circ }\\ \Rightarrow AB \approx 23,96\;(km)\end{array}$ $\begin{array}{l}A{B^2} = {370^2} + {350^2} - 2.370.350.\cos 2,{1^ \circ }\\ \Rightarrow AB \approx 23,96\;(km)\end{array}$

Vậy khoảng cách giữa hai tòa nhà là 23,96 km.

Bài 9 trang 79

Hai chiếc tàu thủy P và Q cách nhau 300m và thẳng hàng với chân B của tháp hải đăng AB ở trên bờ biển (Hình 2). Từ P và Q, người ta nhìn thấy tháp hải đăng AB dưới các góc $\widehat {BPA} = {35^o}$ $\widehat {BPA} = {35^o}$ và $\widehat {BQA} = {48^o}.$ $\widehat {BQA} = {48^o}.$ Tính chiều cao của tháp hải đăng đó.

Gợi ý đáp án

Xét tam giác APB và AQB, ta có:

$\tan {35^ \circ } = \frac{{AB}}{{PB}} = \frac{{AB}}{{300 + QB}} và \tan {48^ \circ } = \frac{{AB}}{{QB}}$ $\tan {35^ \circ } = \frac{{AB}}{{PB}} = \frac{{AB}}{{300 + QB}} và \tan {48^ \circ } = \frac{{AB}}{{QB}}$

$\begin{array}{l} \Rightarrow AB = \tan {35^ \circ }.\left( {300 + QB} \right) = \tan {48^ \circ }.QB\\ \Leftrightarrow \tan {35^ \circ }.300 + \tan {35^ \circ }.QB = \tan {48^ \circ }.QB\\ \Leftrightarrow \tan {35^ \circ }.300 = \left( {\tan {{48}^ \circ } - \tan {{35}^ \circ }} \right).QB\\ \Leftrightarrow QB = \frac{{\tan {{35}^ \circ }.300}}{{\tan {{48}^ \circ } - \tan {{35}^ \circ }}}\end{array}$ $\begin{array}{l} \Rightarrow AB = \tan {35^ \circ }.\left( {300 + QB} \right) = \tan {48^ \circ }.QB\\ \Leftrightarrow \tan {35^ \circ }.300 + \tan {35^ \circ }.QB = \tan {48^ \circ }.QB\\ \Leftrightarrow \tan {35^ \circ }.300 = \left( {\tan {{48}^ \circ } - \tan {{35}^ \circ }} \right).QB\\ \Leftrightarrow QB = \frac{{\tan {{35}^ \circ }.300}}{{\tan {{48}^ \circ } - \tan {{35}^ \circ }}}\end{array}$

Mà $AB = \tan {48^ \circ }.QB$ $AB = \tan {48^ \circ }.QB$

$\Rightarrow AB = \tan {48^ \circ }.\frac{{\tan {{35}^ \circ }.300}}{{\tan {{48}^ \circ } - \tan {{35}^ \circ }}} \approx 568,5\;(m)$ $\Rightarrow AB = \tan {48^ \circ }.\frac{{\tan {{35}^ \circ }.300}}{{\tan {{48}^ \circ } - \tan {{35}^ \circ }}} \approx 568,5\;(m)$

Vậy tháp hải đăng cao khoảng 568,5 m.

Bài 10 trang 79

Muốn đo chiều cao của một ngọn tháp, người ta lấy hai điểm A, B trên mặt đất có khoảng cách AB = 12m cùng thẳng hàng với chân C của tháp để đặt hai giác kế. Chân của hai giác kế có chiều cao là h = 1,2m. Gọi D là đỉnh tháp và hai điểm ${A_1},{B_1}$ ${A_1},{B_1}$ cùng thẳng hàng với ${C_1}$ ${C_1}$ thuộc chiều cao CD của tháp. Người ta do được $\widehat {D{A_1}{C_1}} = {49^ \circ },\widehat {D{B_1}{C_1}} = {35^ \circ }$ $\widehat {D{A_1}{C_1}} = {49^ \circ },\widehat {D{B_1}{C_1}} = {35^ \circ }$. Tính chiều cao CD của tháp.

Gợi ý đáp án

Ta có: $\widehat {D{A_1}{C_1}} = \widehat {{A_1}D{B_1}} + \widehat {D{B_1}{A_1}} \Rightarrow \widehat {{A_1}D{B_1}} = {49^ \circ } - {35^ \circ } = {14^ \circ }$ $\widehat {D{A_1}{C_1}} = \widehat {{A_1}D{B_1}} + \widehat {D{B_1}{A_1}} \Rightarrow \widehat {{A_1}D{B_1}} = {49^ \circ } - {35^ \circ } = {14^ \circ }$

Áp dụng định lí sin trong tam giác ${A_1}D{B_1}$ ${A_1}D{B_1}$ , ta có:

$\begin{array}{l}\frac{{{A_1}D}}{{\sin {B_1}}} = \frac{{{A_1}{B_1}}}{{\sin D}} \Leftrightarrow \frac{{{A_1}D}}{{\sin {{35}^ \circ }}} = \frac{{12}}{{\sin {{14}^ \circ }}}\\ \Rightarrow {A_1}D = \sin {35^ \circ }.\frac{{12}}{{\sin {{14}^ \circ }}} \approx 28,45\end{array}$ $\begin{array}{l}\frac{{{A_1}D}}{{\sin {B_1}}} = \frac{{{A_1}{B_1}}}{{\sin D}} \Leftrightarrow \frac{{{A_1}D}}{{\sin {{35}^ \circ }}} = \frac{{12}}{{\sin {{14}^ \circ }}}\\ \Rightarrow {A_1}D = \sin {35^ \circ }.\frac{{12}}{{\sin {{14}^ \circ }}} \approx 28,45\end{array}$

Áp dụng định lí sin trong tam giác ${A_1}D{C_1}$ ${A_1}D{C_1}$ , ta có:

$\begin{array}{l}\frac{{{A_1}D}}{{\sin {C_1}}} = \frac{{{C_1}D}}{{\sin {A_1}}} \Leftrightarrow \frac{{28,45}}{{\sin {{90}^ \circ }}} = \frac{{{C_1}D}}{{\sin {{49}^ \circ }}}\\ \Rightarrow {C_1}D = \sin {49^ \circ }.\frac{{28,45}}{{\sin {{90}^ \circ }}} \approx 21,47\end{array}$ $\begin{array}{l}\frac{{{A_1}D}}{{\sin {C_1}}} = \frac{{{C_1}D}}{{\sin {A_1}}} \Leftrightarrow \frac{{28,45}}{{\sin {{90}^ \circ }}} = \frac{{{C_1}D}}{{\sin {{49}^ \circ }}}\\ \Rightarrow {C_1}D = \sin {49^ \circ }.\frac{{28,45}}{{\sin {{90}^ \circ }}} \approx 21,47\end{array}$

Do đó, chiều cao CD của tháp là: 21,47 + 1,2 = 22,67;(m)

Chia sẻ bởi: