Toán 6 Luyện tập chung trang 25 Giải Toán lớp 6 trang 25, 26 sách Kết nối tri thức với cuộc sống - Tập 2

Tải về

Giải Toán 6 Luyện tập chung giúp các em học sinh lớp 6 tham khảo đáp án của 6 bài tập SGK Toán 6 Kết nối tri thức với cuộc sống tập 2 trang 25, 26. Qua đó, giúp các em biết cách thực hiện phép cộng phân số, phép trừ phân số, phép nhân phân số, phép chia phân số.

Đồng thời, cũng giúp thầy cô soạn giáo án bài Luyện tập chung trang 25 Chương VI: Phân số - Toán 6 tập 2 Kết nối tri thức với cuộc sống cho học sinh của mình. Mời thầy cô và các em cùng tải miễn phí bài viết:

Giải Toán 6 bài Luyện tập chung trang 25 Kết nối tri thức với cuộc sống

Giải Toán 6 Kết nối tri thức với cuộc sống trang 25 tập 2

Bài 6.38

Tính:

a. $\frac{-1}{2}+\frac{5}{6}+\frac{1}{3}$ $\frac{-1}{2}+\frac{5}{6}+\frac{1}{3}$;

c. $\frac{3}{5}: (\frac{1}{4}.\frac{7}{5})$ $\frac{3}{5}: (\frac{1}{4}.\frac{7}{5})$;

b. $\frac{-3}{8}+\frac{7}{4}-\frac{1}{12}$ $\frac{-3}{8}+\frac{7}{4}-\frac{1}{12}$;

d. $\frac{10}{11}+\frac{4}{11}:4-\frac{1}{8}$ $\frac{10}{11}+\frac{4}{11}:4-\frac{1}{8}$.

Hướng dẫn giải

Thứ tự thực hiện phép tính: Nhân chia trước, cộng trừ sau
Tính chất giao hoán: a + b = b + a

Tính chất kết hợp: (a + b) + c = a + (b + c)

Tính chất phân phối của phép nhân đối với phép cộng: a . (b + c) = ab + ac
Muốn cộng hai phân số không cùng mẫu, ta thực hiện quy đồng mẫu số các phân số đưa chúng về dạng hai phân số cùng mẫu rồi cộng các tử, giữ nguyên mẫu.
Muốn trừ hai phân số không cùng mẫu, ta thực hiện quy đồng mẫu số các phân số đưa chúng về dạng hai phân số cùng mẫu rồi trừ hai phân số đó.

Gợi ý đáp án:

a. $\frac{-1}{2}+\frac{5}{6}+\frac{1}{3}=\frac{-3}{6}+\frac{5}{6}+\frac{2}{6}=\frac{2}{3}$ $\frac{-1}{2}+\frac{5}{6}+\frac{1}{3}=\frac{-3}{6}+\frac{5}{6}+\frac{2}{6}=\frac{2}{3}$.

b. $\frac{-3}{8}+\frac{7}{4}-\frac{1}{12}=\frac{-9}{24}+\frac{42}{24}-\frac{2}{24}=\frac{31}{24}$ $\frac{-3}{8}+\frac{7}{4}-\frac{1}{12}=\frac{-9}{24}+\frac{42}{24}-\frac{2}{24}=\frac{31}{24}$.

c. $\frac{3}{5}:(\frac{1}{4}.\frac{7}{5})=\frac{3}{5}:\frac{7}{20}=\frac{3}{5}.\frac{20}{7}=\frac{12}{7}$ $\frac{3}{5}:(\frac{1}{4}.\frac{7}{5})=\frac{3}{5}:\frac{7}{20}=\frac{3}{5}.\frac{20}{7}=\frac{12}{7}$.

d. $\frac{10}{11}+\frac{4}{11}:4-\frac{1}{8}=(\frac{10}{11}+\frac{1}{11})-\frac{1}{8}=1-\frac{1}{8}=\frac{7}{8}$ $\frac{10}{11}+\frac{4}{11}:4-\frac{1}{8}=(\frac{10}{11}+\frac{1}{11})-\frac{1}{8}=1-\frac{1}{8}=\frac{7}{8}$.

Bài 6.39

Tính một cách hợp lí.

$B= \frac{5}{13}.\frac{8}{15}+\frac{5}{13}.\frac{26}{15}-\frac{5}{13}.\frac{8}{15}$ $B= \frac{5}{13}.\frac{8}{15}+\frac{5}{13}.\frac{26}{15}-\frac{5}{13}.\frac{8}{15}$.

Gợi ý đáp án:

$B= \frac{5}{13}.\frac{8}{15}+\frac{5}{13}.\frac{26}{15}-\frac{5}{13}.\frac{8}{15}$ $B= \frac{5}{13}.\frac{8}{15}+\frac{5}{13}.\frac{26}{15}-\frac{5}{13}.\frac{8}{15}$

$B=\frac{5}{13}.(\frac{8}{15}+\frac{26}{15}-\frac{8}{15})$ $B=\frac{5}{13}.(\frac{8}{15}+\frac{26}{15}-\frac{8}{15})$

$B=\frac{5}{13}.\frac{26}{15}$ $B=\frac{5}{13}.\frac{26}{15}$

$B=\frac{2}{3}$ $B=\frac{2}{3}$

Bài 6.40

Tính giá trị của biểu thức sau:

$B=\frac{1}{3}.b+\frac{2}{9}.b-b:\frac{4}{9}$ $B=\frac{1}{3}.b+\frac{2}{9}.b-b:\frac{4}{9}$ với $b=\frac{9}{10}$ $b=\frac{9}{10}$.

Hướng dẫn giải

Thứ tự thực hiện phép tính: Nhân chia trước, cộng trừ sau
Muốn nhân hai phân số, ta nhân các tử với nhau và nhân các mẫu với nhau.
Muốn chia một phân số cho một phân số khác 0, ta nhân số bị chia với phân số nghịch đảo của số chia.

Gợi ý đáp án:

Với $b=\frac{9}{10}$ $b=\frac{9}{10}$, ta có:

$B=\frac{1}{3}.\frac{9}{10}+\frac{2}{9}.\frac{9}{10}-\frac{9}{10}:\frac{4}{9}$ $B=\frac{1}{3}.\frac{9}{10}+\frac{2}{9}.\frac{9}{10}-\frac{9}{10}:\frac{4}{9}$

$B=\frac{3}{10}+\frac{1}{5}-\frac{2}{5}$ $B=\frac{3}{10}+\frac{1}{5}-\frac{2}{5}$

$B=\frac{3}{10}-\frac{1}{5}=\frac{3}{10}-\frac{2}{10}=\frac{1}{10}$ $B=\frac{3}{10}-\frac{1}{5}=\frac{3}{10}-\frac{2}{10}=\frac{1}{10}$.

Bài 6.41

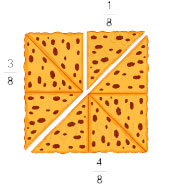
Nam cắt một chiếc bánh nướng hình vuông thành ba phần không bằng nhau (như hình vẽ). Nam đã ăn hai phần bánh, tổng cộng $\frac{1}{2}$ $\frac{1}{2}$ chiếc bánh. Đố em biết Nam đã ăn hai phần bánh nào?

Bài 6.41

Hướng dẫn giải

- Muốn tìm $\frac{m}{n}$ $\frac{m}{n}$ của một số a cho trước ta tính $a.\frac{m}{n};\left( {m \in \mathbb{N},n \in {\mathbb{N}^*}} \right)$ $a.\frac{m}{n};\left( {m \in \mathbb{N},n \in {\mathbb{N}^*}} \right)$

- Muốn tìm $\frac{m}{n}$ $\frac{m}{n}$ của một số b cho trước ta tính $b:\frac{m}{n};\left( {m,n \in {\mathbb{N}^*}} \right)$ $b:\frac{m}{n};\left( {m,n \in {\mathbb{N}^*}} \right)$

- Muốn nhân hai phân số, ta nhân các tử với nhau và nhân các mẫu với nhau.

- Muốn chia một phân số cho một phân số khác 0, ta nhân số bị chia với phân số nghịch đảo của số chia.

Gợi ý đáp án:

Ta có: $\frac{1}{8}+\frac{3}{8}=\frac{1}{2}$ $\frac{1}{8}+\frac{3}{8}=\frac{1}{2}$

Nên Nam đã ăn hai phần bánh là $\frac{1}{8}$ $\frac{1}{8}$ và $\frac{3}{8}$ $\frac{3}{8}$.

Bài 6.42

Để làm một chiếc bánh chưng trong dịp Tết cổ truyền, Vân phải chuẩn bị: Gạo nếp, đậu xanh không vỏ, thịt ba chỉ, lá dong và các gia vị khác. Khối lượng đậu xanh bằng $\frac{3}{5}$ $\frac{3}{5}$ khối lượng gạo nếp và gấp $\frac{3}{2}$ $\frac{3}{2}$ khối lượng thịt ba chỉ. Nếu có 150 gam đậu xanh thì cần bao nhiêu gam gạo nếp và bao nhiêu gam thịt ba chỉ?

Gợi ý đáp án:

Nếu có 150 gam đậu xanh thì cần số gạo nếp là: $150:\frac{3}{5}=250$ $150:\frac{3}{5}=250$ gam

Nếu có 150 gam đậu xanh thì cần số thịt ba chỉ là: $150:\frac{3}{2}=100$ $150:\frac{3}{2}=100$ gam

Bài 6.43

Hà thường đi xe đạp từ nhà đến trường với vận tốc 12 km/h, hết $\frac{1}{5}$ $\frac{1}{5}$ giờ. Hôm nay xe đạp bị hỏng nên Hà phải đi bộ đến trường với vận tốc 5 km/h. Hỏi hôm nay Hà đi đến trường mất bao lâu?

Hướng dẫn giải

- Quãng đường tính bằng vận tốc nhân với thời gian.

=> Thời gian bằng quãng đường chia cho vận tốc.

- Muốn nhân hai phân số, ta nhân các tử với nhau và nhân các mẫu với nhau.

- Muốn chia một phân số cho một phân số khác 0, ta nhân số bị chia với phân số nghịch đảo của số chia.

Gợi ý đáp án:

Quãng đường Hà đi đến trường là:

$12.\frac{1}{5}=\frac{12}{5}$ $12.\frac{1}{5}=\frac{12}{5}$ (km)

Thời gian Hà đi đến trường hôm nay là:

$\frac{12}{5}:5=\frac{12}{25}$ $\frac{12}{5}:5=\frac{12}{25}$ (giờ)

Lý thuyết Luyện tập chung trang 25

1. Phép cộng hai phân số

a) Cộng hai phân số cùng mẫu:

Muốn cộng hai phân số cùng mẫu, ta cộng các tử và giữ nguyên mẫu.

$\dfrac{a}{m} + \dfrac{b}{m} = \dfrac{{a + b}}{m}$ $\dfrac{a}{m} + \dfrac{b}{m} = \dfrac{{a + b}}{m}$ $(m \ne 0)$ $(m \ne 0)$

Ví dụ:

$\dfrac{8}{5} + \dfrac{7}{5} = \dfrac{{8 + 7}}{5} = \dfrac{{15}}{5} = 3$ $\dfrac{8}{5} + \dfrac{7}{5} = \dfrac{{8 + 7}}{5} = \dfrac{{15}}{5} = 3$

b) Cộng hai phân số khác mẫu:

Muốn cộng hai phân số khác mẫu, ta viết chúng dưới dạng hai phân số cùng mẫu rồi cộng các tử với nhau và giữ nguyên mẫu chung.

Ví dụ:

$\dfrac{3}{2} + \dfrac{{ - 3}}{5} = \dfrac{{15}}{{10}} + \dfrac{{ - 6}}{{10}} = \dfrac{{15 + \left( { - 6} \right)}}{{10}} = \dfrac{9}{{10}}$ $\dfrac{3}{2} + \dfrac{{ - 3}}{5} = \dfrac{{15}}{{10}} + \dfrac{{ - 6}}{{10}} = \dfrac{{15 + \left( { - 6} \right)}}{{10}} = \dfrac{9}{{10}}$

2. Phép trừ hai phân số

- Muốn trừ hai phân số cùng mẫu ta lấy tử của phân số thứ nhất trừ đi tử của phân số thứ hai và giữ nguyên mẫu.

$\dfrac{a}{m} - \dfrac{b}{m} = \dfrac{{a - b}}{m}$ $\dfrac{a}{m} - \dfrac{b}{m} = \dfrac{{a - b}}{m}$

- Muốn trừ hai phân số khác mẫu, ta quy đồng hai phân số, rồi trừ hai phân số đó.

Ví dụ:

a) $\dfrac{2}{7} - \dfrac{5}{7} = \dfrac{{2 - 5}}{7} = \dfrac{{ - 3}}{7}$ $\dfrac{2}{7} - \dfrac{5}{7} = \dfrac{{2 - 5}}{7} = \dfrac{{ - 3}}{7}$

b) $\dfrac{1}{6} - \dfrac{1}{2} = \dfrac{1}{6} + \left( { - \dfrac{1}{2}} \right) = \dfrac{1}{6} + \left( {\dfrac{{ - 3}}{6}} \right) = \dfrac{{1 + \left( { - 3} \right)}}{6} = \dfrac{{ - 2}}{6} = \dfrac{{ - 1}}{3}$ $\dfrac{1}{6} - \dfrac{1}{2} = \dfrac{1}{6} + \left( { - \dfrac{1}{2}} \right) = \dfrac{1}{6} + \left( {\dfrac{{ - 3}}{6}} \right) = \dfrac{{1 + \left( { - 3} \right)}}{6} = \dfrac{{ - 2}}{6} = \dfrac{{ - 1}}{3}$

Nhận xét: Muốn trừ một phân số cho một phân số, ta có thể cộng số bị trừ với số đối của số trừ.

3. Phép nhân hai phân số

+ Muốn nhân hai phân số, ta nhân các tử số với nhau và nhân các mẫu với nhau.

$\dfrac{a}{b}.\dfrac{c}{d} = \dfrac{{a.c}}{{b.d}}$ $\dfrac{a}{b}.\dfrac{c}{d} = \dfrac{{a.c}}{{b.d}}$

+ Muốn nhân một số nguyên với một phân số (hoặc một phân số với một số nguyên), ta nhân số nguyên với tử của phân số và giữ nguyên mẫu: $a.\dfrac{b}{c} = \dfrac{{a.b}}{c}$ $a.\dfrac{b}{c} = \dfrac{{a.b}}{c}$

Ví dụ:

a) $\dfrac{{ - 1}}{4}.\dfrac{1}{5} = \dfrac{{\left( { - 1} \right).1}}{{4.5}} = \dfrac{{ - 1}}{{20}}$ $\dfrac{{ - 1}}{4}.\dfrac{1}{5} = \dfrac{{\left( { - 1} \right).1}}{{4.5}} = \dfrac{{ - 1}}{{20}}$

b) $2.\dfrac{4}{5} = \dfrac{{2.4}}{5} = \dfrac{8}{5}$ $2.\dfrac{4}{5} = \dfrac{{2.4}}{5} = \dfrac{8}{5}$

4. Phép chia hai phân số

Muốn chia một phân số hay một số nguyên cho một phân số, ta nhân số bị chia với số nghịch đảo của số chia.

$\dfrac{a}{b}:\dfrac{c}{d} = \dfrac{a}{b}.\dfrac{d}{c} = \dfrac{{a.d}}{{b.c}}$ $\dfrac{a}{b}:\dfrac{c}{d} = \dfrac{a}{b}.\dfrac{d}{c} = \dfrac{{a.d}}{{b.c}}$

$a:\dfrac{c}{d} = a.\dfrac{d}{c} = \dfrac{{a.d}}{c}\left( {c \ne 0} \right)$ $a:\dfrac{c}{d} = a.\dfrac{d}{c} = \dfrac{{a.d}}{c}\left( {c \ne 0} \right)$

Ví dụ: $\dfrac{{ - 1}}{6}:\dfrac{3}{{13}} = \dfrac{{ - 1}}{6}.\dfrac{{13}}{3} = \dfrac{{\left( { - 1} \right).13}}{{6.3}} = \dfrac{{ - 13}}{{18}}$ $\dfrac{{ - 1}}{6}:\dfrac{3}{{13}} = \dfrac{{ - 1}}{6}.\dfrac{{13}}{3} = \dfrac{{\left( { - 1} \right).13}}{{6.3}} = \dfrac{{ - 13}}{{18}}$

Chia sẻ bởi:

Hàn Vũ

Tải về

Bài trước

Bài sau

Liên kết tải về

Toán 6 Luyện tập chung trang 25 236,7 KB

Tải về

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!