Toán 9 Luyện tập chung trang 108 Giải Toán 9 Kết nối tri thức tập 1 trang 108, 109, 110

Giải Toán lớp 9 Luyện tập chung bao gồm đáp án chi tiết cho từng phần, từng bài tập trong SGK Toán 9 Kết nối tri thức với cuộc sống tập 1 trang 108, 109, 110.

Lời giải Toán 9 KNTT trang 108, 109, 110 trình bày khoa học, biên soạn dễ hiểu, giúp các em nâng cao kỹ năng giải Toán 9, từ đó học tốt môn Toán lớp 9 hơn. Đồng thời, cũng giúp thầy cô nhanh chóng soạn giáo án Luyện tập chung Chương V: Đường tròn. Mời thầy cô và các em cùng theo dõi bài viết dưới đây của Eballsviet.com:

Giải Toán 9 Kết nối tri thức Tập 1 trang 109, 110

Bài 5.28

Cho hai đường thẳng a và b song song với nhau, điểm O nằm trong phần mặt phẳng ở giữa hai đường thẳng đó. Biết rằng khoảng cách từ O đến a và b lần lượt bằng 2 cm và 3 cm.

a) Hỏi bán kính của đường tròn (O; R) phải thỏa mãn điều kiện gì để (O; R) cắt cả hai đường thẳng a và b?

b) Biết rằng đường tròn (O; R) tiếp xúc với đường thẳng a. Hãy xác định vị trí tương đối của đường tròn (O; R) và đường thẳng b.

Lời giải:

a) Đường tròn (O; R) cắt cả hai đường thẳng a và b khi và chỉ khi R > 3 cm.

b) Đường tròn (O; R) tiếp xúc với đường thẳng a nên R = 2 cm < 3 cm.

Do đó (O; R) cắt đường thẳng b.

Bài 5.29

Khi chuyển động, giả sử đầu mũi kim dài của một chiếc đồng hồ vạch nên một đường tròn, kí hiệu là (T1), trong khi đầu mũi kim ngắn vạch nên một đường tròn khác, kí hiệu là (T2).

a) Hai đường tròn (T1) và (T2) có vị trí tương đối như thế nào?

b) Giả sử bán kính của (T1) và (T2) lần lượt là R1 và R2. Người ta vẽ trên mặt đồng hồ một họa tiết hình tròn có tâm nằm cách điểm trục kim đồng hồ một khoảng bằng \(\frac{1}{2}\)R1 và có bán kính bằng \(\frac{1}{2}\)R2. Hãy cho biết vị trí tương đối của đường tròn (T3) đối với mỗi đường tròn (T1) và (T2). Vẽ ba đường tròn đó nếu R1 = 3 cm, R2 = 2 cm.

Bài 5.30

Cho đường tròn (O) đường kính AB, tiếp tuyến xx' tại A và tiếp tuyến yy' tại B của (O). Một tiếp tuyến thứ ba của (O) tại điểm P (P khác A và B) cắt xx' tại M và cắt yy' tại N.

a) Chứng minh rằng MN = MA + NB.

b) Đường thẳng đi qua O và vuông góc với AB cắt NM tại Q. Chứng minh rằng Q là trung điểm của đoạn MN.

c) Chứng minh rằng AB tiếp xúc với đường tròn đường kính MN.

Lời giải:

a) MA và MC là hai tiếp tuyến cắt nhau của (O) nên MA = MC.

NB và NC là hai tiếp tuyến cắt nhau của (O) nên NA = NC.

Ta có: MN = MC + NC = MA + NB

b) Gọi K là giao điểm của AN và OQ.

Ta có: BN // OK (vì cùng vuông góc với AB) và O là trung điểm của AB.

Suy ra OK là đường trung bình của tam giác ABN.

Do đó K là trung điểm của AN.

Lại có: AM // QK (vì cùng vuông góc với AB) và K là trung điểm của AN.

Suy ra QK là đường trung bình của tam giác AMN.

Do đó Q là trung điểm của MN.

c) OK là đường trung bình của tam giác ABN nên OK= \(\frac{1}{2}\)NB.

QK là đường trung bình của tam giác AMN nên QK=\(\frac{1}{2}\)MA.

Suy ra: OQ=OK+QK=\(\frac{1}{2}\)NB+\(\frac{1}{2}\)MA=\(\frac{1}{2}\)MN hay OQ = AQ = BQ.

Do đó O thuộc đường tròn đường kính MN.

Bài 5.31

Cho đường tròn (O) và (O') tiếp xúc ngoài với nhau tại A và cùng tiếp xúc với đường thẳng d tại B và C (khác A), trong đó B ∈ (O) và C ∈ (O′). Tiếp tuyến của (O) tại A cắt BC tại M. Chứng minh rằng:

a) Đường thẳng MA tiếp xúc với (O');

b) Điểm M là trung điểm của đoạn thẳng BC, từ đó suy ra ABC là tam giác vuông.

Lời giải:

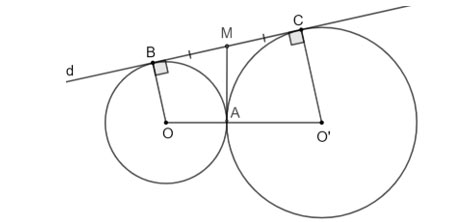
a) A thuộc (O') và O'A vuông góc với MA nên MA là tiếp tuyến tại A của (O).

b) MA và MB là hai tiếp tuyến cắt nhau của (O) nên MA = MB.

MA và MC là hai tiếp tuyến cắt nhau của (O) nên MA = MC.

Suy ra MB = MC = MA hay M là trung điểm của BC.

Do đó tam giác ABC vuông tại A.