Eballsviet.com Học tập Lớp 9 Toán 9 Kết nối tri thức

Toán 9 Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng Giải Toán 9 Kết nối tri thức tập 1 trang 74, 75 76, 77, 78

Tải về Bình luận
  • 9
Mục lục

Giải Toán 9 Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng là tài liệu vô cùng hữu ích giúp các em học sinh lớp 9 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 9 Kết nối tri thức với cuộc sống tập 1 trang 74, 75 76, 77, 78.

Giải bài tập Toán 9 Kết nối tri thức tập 1 trang 74 → 78 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh ôn tập Bài 12 Chương IV: Hệ thức lượng trong tam giác vuông. Mời thầy cô và các em theo dõi bài viết dưới đây của Eballsviet.com:

Toán 9 Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng Kết nối tri thức

Giải Toán 9 Kết nối tri thức Tập 1 trang 78

Bài 4.8

Giải tam giác ABC vuông tại A có BC = a,AC = b,AB = c, trong các trường hợp:

a) a = 21, b = 18;

b) b = 10,\widehat C = {30^0};\(\widehat C = {30^0};\)

c) c = 5, b = 3.

Lời giải:

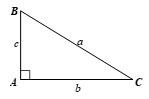
Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng

a) a = 21,b = 18;

Tam giác ABC vuông tại A, ta có: A{B^2} + A{C^2} = B{C^2}\(A{B^2} + A{C^2} = B{C^2}\) (định lý Pythagore)

Thay số ta có: A{B^2} + {18^2} = {21^2}\(A{B^2} + {18^2} = {21^2}\) hay AB = \sqrt {{{21}^2} - {{18}^2}} = 3\sqrt {13}\(AB = \sqrt {{{21}^2} - {{18}^2}} = 3\sqrt {13}\)(vì AB > 0)

Ta có \sin \widehat B = \frac{{AC}}{{BC}} = \frac{{18}}{{21}} = \frac{6}{7}\(\sin \widehat B = \frac{{AC}}{{BC}} = \frac{{18}}{{21}} = \frac{6}{7}\)nên\widehat B \approx {59^0}\(\widehat B \approx {59^0}\)

Mà \widehat B + \widehat C = {90^0}\(\widehat B + \widehat C = {90^0}\) nên \widehat C = {90^0} - \widehat B \approx {90^0} - {59^0} = {31^0}\(\widehat C = {90^0} - \widehat B \approx {90^0} - {59^0} = {31^0}\)

b) b = 10,\widehat C = {30^0};\(\widehat C = {30^0};\)

Tam giác ABC vuông tại A, ta có \tan \widehat C = \frac{{AC}}{{AB}}\(\tan \widehat C = \frac{{AC}}{{AB}}\) hay \tan {30^0} = \frac{{10}}{{AB}}\(\tan {30^0} = \frac{{10}}{{AB}}\) suy ra AB = \frac{{10}}{{\tan {{30}^0}}} = 10\sqrt 3\(AB = \frac{{10}}{{\tan {{30}^0}}} = 10\sqrt 3\)

\sin \widehat C = \frac{{AC}}{{BC}}\(\sin \widehat C = \frac{{AC}}{{BC}}\) hay \sin {30^0} = \frac{{10}}{{BC}}\(\sin {30^0} = \frac{{10}}{{BC}}\) suy ra BC = \frac{{10}}{{\sin {{30}^0}}} = 20\(BC = \frac{{10}}{{\sin {{30}^0}}} = 20\)

Mà \widehat B + \widehat C = {90^0} nên \widehat C = {90^0} - \widehat B = {90^0} - {30^0} = {60^0}\(\widehat B + \widehat C = {90^0} nên \widehat C = {90^0} - \widehat B = {90^0} - {30^0} = {60^0}\)

c) c = 5,b = 3.

Tam giác ABC vuông tại A, ta có: A{B^2} + A{C^2} = B{C^2}\(A{B^2} + A{C^2} = B{C^2}\) (định lý Pythagore)

Thay số ta có: B{C^2} = {5^2} + {3^2} = 34\(B{C^2} = {5^2} + {3^2} = 34\) hay BC = \sqrt {34} (vì BC > 0)\(BC = \sqrt {34} (vì BC > 0)\)

Ta có \sin \widehat B = \frac{{AC}}{{BC}} = \frac{3}{{\sqrt {34} }} nên \widehat B \approx {30^0}58\(\sin \widehat B = \frac{{AC}}{{BC}} = \frac{3}{{\sqrt {34} }} nên \widehat B \approx {30^0}58'\)

Mà \widehat B + \widehat C = {90^0}\(\widehat B + \widehat C = {90^0}\) nên \widehat C = {90^0} - \widehat B \approx {90^0} - {30^0}57\(\widehat C = {90^0} - \widehat B \approx {90^0} - {30^0}57' = {59^0}02'\)

Bài 4.9

Tính góc nghiêng α của thùng xe chở rác trong Hình 4.22.

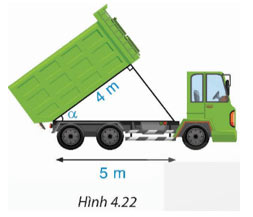
Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng

Lời giải:

Theo định nghĩa tỉ số lượng giác cos, ta có cosα=4/5\(cosα=4/5\), từ đó tính được α ≈ 36°52’.

Vậy góc nghiêng α của thùng xe chở rác khoảng 36°52’.

Bài 4.10

Tìm góc nghiêng α và chiều rộng AB của mái nhà kho trong Hình 4.23.

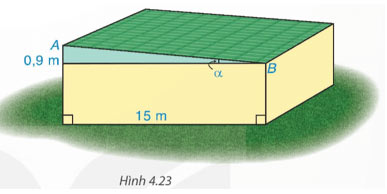
Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng

Lời giải:

Ta có: \tan \alpha = \frac{{0,9}}{{15}}\(\tan \alpha = \frac{{0,9}}{{15}}\) hay \alpha \approx {3^0}26\(\alpha \approx {3^0}26'\)

Độ dài cạnh AB là AB = \sqrt {0,{9^2} + {{15}^2}} = \sqrt {225,81} \approx 15,03 m\(\sqrt {0,{9^2} + {{15}^2}} = \sqrt {225,81} \approx 15,03 m\)

Vậy góc nghiêng \alpha của mái nhà kho khoảng {3^0}26\({3^0}26'\) và chiều rộng AB \approx 15,03\(AB \approx 15,03\)

Bài 4.11

Tính các góc của hình thoi có hai đường chéo dài 2\sqrt 3\(2\sqrt 3\) và 2.

Lời giải:

Xét hình thoi ACBE có hai đường chéo ED và đường chéo AB lần lượt là 2\sqrt 3\(2\sqrt 3\) và 2.

Hai đường chéo cắt nhau tại C nên C là trung điểm của hai đường chéo

Do đó: CE = CD = \sqrt 3\(CE = CD = \sqrt 3\) ;AC = CB = 1

Tam giác ACD vuông tại C (tính chất hai đường chéo của hình thoi) ta có:

CE = CD = \sqrt 3\(CE = CD = \sqrt 3\) hay \widehat {DAC} = {60^0}\(\widehat {DAC} = {60^0}\) nên \widehat {DAE} = 2\widehat {DAC} = {2.60^0} = {120^0}\(\widehat {DAE} = 2\widehat {DAC} = {2.60^0} = {120^0}\) (tính chất hình thoi)

\widehat {DAC} + \widehat {ADC} = {90^0}\(\widehat {DAC} + \widehat {ADC} = {90^0}\) (Do tam giác ACD vuông tại C)

Nên\widehat {ADC} = {90^0} - {60^0} = {30^0}\(\widehat {ADC} = {90^0} - {60^0} = {30^0}\) nên \widehat {ADB} = 2.\widehat {ADC} = {2.30^0} = {60^0}\(\widehat {ADB} = 2.\widehat {ADC} = {2.30^0} = {60^0}\)

Vậy hình thoi có các góc là 1200 và 600

Bài 4.12

Cho hình thang ABCD (AD // BC) có AD = 16cm,BC = 4cm,\widehat A = \widehat B = \widehat {ACD} = {90^0}.\(\widehat A = \widehat B = \widehat {ACD} = {90^0}.\)

a) Kẻ đường cao CE của tam giác ACD. Chứng minh \widehat {ADC} = \widehat {ACE}. Tính sin của các góc \widehat {ADC},\widehat {ACE} và suy ra A{C^2} = AE.AD. Từ đó tính AC.

b) Tính góc D của hình thang.

Lời giải:

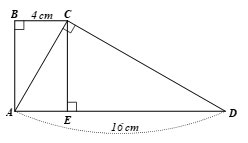
Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng

a) Ta có \widehat {ADC} = \widehat {ACE}\(\widehat {ADC} = \widehat {ACE}\) (cùng phụ với góc DCE)

Ta có \sin \widehat {ADC} = \frac{{AC}}{{AD}};\sin \widehat {ACE} = \frac{{AE}}{{AC}}\(\sin \widehat {ADC} = \frac{{AC}}{{AD}};\sin \widehat {ACE} = \frac{{AE}}{{AC}}\). Từ đó ta có \frac{{AC}}{{AD}} = \frac{{AE}}{{AC}}\(\frac{{AC}}{{AD}} = \frac{{AE}}{{AC}}\) hay A{C^2} = AE.AD.\(A{C^2} = AE.AD.\)

AECB là hình chữ nhật do \widehat {BAE} = \widehat {ABC} = \widehat {AEC} = {90^0}\(\widehat {BAE} = \widehat {ABC} = \widehat {AEC} = {90^0}\) do đó ta có AE = BC = 4 cm.

Nên A{C^2} = AE.AD = 4.16 = 64\(A{C^2} = AE.AD = 4.16 = 64\) hay AC = \sqrt {64} = 8 cm (vì AC > 0)\(AC = \sqrt {64} = 8 cm (vì AC > 0)\)

b) \sin \widehat {ADC} = \frac{{AC}}{{AD}}\(\sin \widehat {ADC} = \frac{{AC}}{{AD}}\) hay \sin \widehat {ADC} = \frac{8}{{16}} = \frac{1}{2}\(\sin \widehat {ADC} = \frac{8}{{16}} = \frac{1}{2}\) hay \sin \widehat {ADC} = {30^0}\(\sin \widehat {ADC} = {30^0}\)

Bài 4.13

Một người đứng tại điểm A, cách gương phẳng đặt nằm trên mặt đất tại điểm B là 1,2 m, nhìn thấy hình phản chiếu qua gương B của ngọn cây (cây có gốc ở tại điểm C cách B là 4,8 m, B nằm giữa A và C). Biết khoảng cách từ mặt đất đến mắt người đó là 1,65 m. Tính chiều cao của cây (H.4.24).

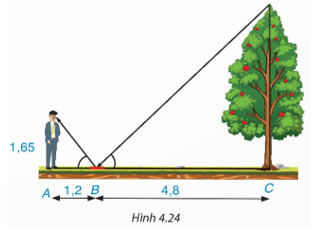
Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng

Lời giải:

Gọi D là điểm tại mắt của người đứng, E là điểm trên đầu ngọn cây, ta có hình vẽ sau;

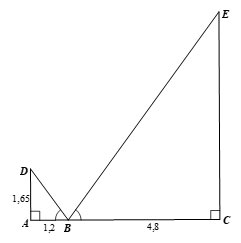
Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng

Chiều cao của cây là đoạn EC

Ta có \tan \widehat {ABD} = \frac{{1,65}}{{1,2}} = \frac{{11}}{8}\(\tan \widehat {ABD} = \frac{{1,65}}{{1,2}} = \frac{{11}}{8}\) hay \tan \widehat {EBC} = \frac{{11}}{8}\(\tan \widehat {EBC} = \frac{{11}}{8}\) (do\widehat {ABC} = \widehat {DBC})\(\widehat {ABC} = \widehat {DBC})\)

Mà \tan \widehat {EBC} = \frac{{EC}}{{BC}}\(\tan \widehat {EBC} = \frac{{EC}}{{BC}}\) suy ra \frac{{EC}}{{4,8}} = \frac{{11}}{8}\(\frac{{EC}}{{4,8}} = \frac{{11}}{8}\) hay EC = \frac{{11}}{8}.4,8 = 6,6 m\(EC = \frac{{11}}{8}.4,8 = 6,6 m\)

Vậy chiều cao của cây là 6,6 m.

Chia sẻ bởi: 👨 Tiểu Hy
Liên kết tải về

Link Download chính thức:

Tìm thêm: Toán lớp 9 Toán 9 Giải SGK Toán 9 Kết nối tri thức với cuộc sống
Sắp xếp theo
👨

Tài liệu tham khảo khác

Chủ đề liên quan

Có thể bạn quan tâm

Xem thêm

Mới nhất trong tuần

Toán 9 - Kết nối tri thức
Chỉ thành viên Download Pro tải được nội dung này! Download Pro - Tải nhanh, website không quảng cáo! Tìm hiểu thêm
Mua Download Pro 79.000đ