Toán 9 Bài tập cuối chương V Giải Toán 9 Kết nối tri thức tập 1 trang 112, 113

Giải Toán lớp 9 Bài tập cuối chương V bao gồm đáp án chi tiết cho từng phần, từng bài tập trong SGK Toán 9 Kết nối tri thức với cuộc sống tập 1 trang 112, 113.

Lời giải Toán 9 KNTT trang 112, 113 trình bày khoa học, biên soạn dễ hiểu, giúp các em nâng cao kỹ năng giải Toán 9, từ đó học tốt môn Toán lớp 9 hơn. Đồng thời, cũng giúp thầy cô nhanh chóng soạn giáo án Bài tập cuối chương V: Đường tròn. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Eballsviet.com:

Giải Toán 9 Kết nối tri thức Tập 1 trang 112 - Trắc nghiệm

Bài 5.32

Cho đường tròn (O; 4 cm) và hai điểm A, B. Biết rằng OA=\(\sqrt{15}\) cm và OB = 4 cm. Khi đó:

A. Điểm A nằm trong (O), điểm B nằm ngoài (O).

B. Điểm A nằm ngoài (O), điểm B nằm trên (O).

C. Điểm A nằm trên (O), điểm B nằm trong (O).

D. Điểm A nằm trong (O), điểm B nằm trên (O).

Đáp án đúng là: D

Bài 5.33

Cho hình 5.43, trong đó BD là đường kính, \(\hat{AOB}\) =40°;  \(\hat{BOC}\)=100°.

Khi đó:

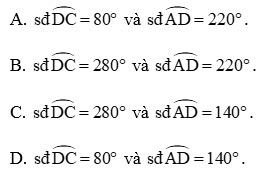
Bài 5.34

Cho hai đường tròn (A; R1), (B; R2), trong đó R2 < R1. Biết rằng hai đường tròn (A) và (B) cắt nhau (H.5.44).

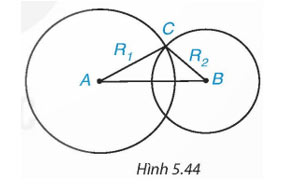
Khi đó:

A. AB < R1 − R2.

B. R1 − R2 < AB < R1 + R2.

C. AB > R1 + R2.

D. AB = R1 + R2.

Đáp án đúng là: B

Bài 5.35

Cho đường tròn (O; R) và hai đường thẳng a1 và a2. Gọi d1, d2 lần lượt là khoảng cách từ điểm O đến a1 và a2. Biết rằng (O) cắt a1 và tiếp xúc với a2 (H.5.45).

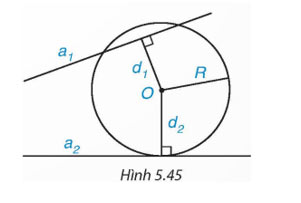
Khi đó:

A. d1 < R, d2 = R.

B. d1 = R, d2 < R.

C. d1 > R, d2 = R.

D. d1 < R, d2 < R.

Đáp án đúng là: A

Giải Toán 9 Kết nối tri thức Tập 1 trang 112, 113 - Tự luận

Bài 5.36

Cho đường tròn (O) đường kính BC và điểm A (khác B và C).

a) Chứng minh rằng nếu A nằm trên (O) thì ABC là một tam giác vuông; ngược lại, nếu ABC là tam giác vuông tại A thì nằm trên (O).

b) Giả sử A là một trong hai giao điểm của đường tròn (B; BO) với đường tròn (O). Tính các góc của tam giác ABC.

c) Với cùng giả thiết câu b), tính độ dài cung AC và diện tích hình quạt nằm trong (O) giới hạn bởi các bán kính OA và OC, biết rằng BC = 6 cm.

Bài 5.37

Cho AB là một dây bất kì (không phải là đường kính) của đường tròn (O; 4 cm). Gọi C và D lần lượt là các điểm đối xứng với A và B qua tâm O.

a) Hai điểm C và D có nằm trên đường tròn (O) không? Vì sao?

b) Biết rằng ABCD là một hình vuông. Tính độ dài cung lớn AB và diện tích hình quạt tròn tạo bởi hai bán kính OA và OB.

Bài 5.38

Cho điểm B nằm giữa hai điểm A và C, sao cho AB = 2 cm và BC = 1 cm. Vẽ các đường tròn (A; 1,5 cm), (B; 3 cm) và (C; 2 cm). Hãy xác định các cặp đường tròn:

a) Cắt nhau;

b) Không giao nhau;

c) Tiếp xúc với nhau.

Lời giải:

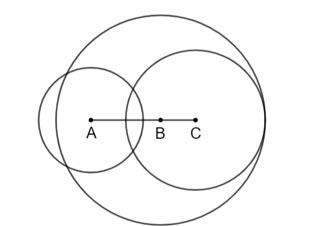
a) Cặp đường thẳng cắt nhau: (A) và (B); (A) và (C).

b) Không có cặp đường tròn nào không giao nhau.

c) Tiếp xúc với nhau: (B) và (C).

Bài 5.39

Cho tam giác vuông ABC ( góc A vuông). Vẽ hai đường tròn (B; BA) và (C; CA) cắt nhau tại A và A'. Chứng minh rằng:

a) BA và BA' là hai tiếp tuyến cắt nhau của (C; CA).

b) CA và CA' là hai tiếp tuyến cắt nhau của (B; BA).

Lời giải:

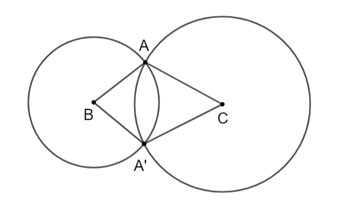
a) Xét ΔABC và ΔA'BC có:

BA = BA'

BC chung

CA = CA'

Do đó ΔABC = ΔA'BC (c.c.c).

Suy ra \(\hat{BAC} = \hat{BA'C}\)=90° (hai góc tương ứng)

Khi đó CA′ ⊥ BA′ tại A′ nên BA′ là tiếp tuyến của (C; CA)

Lại có: CA ⊥ BA tại A nên BA là tiếp tuyến của (C; CA)

Vậy CA và CA′ là hai tiếp tuyến cắt nhau của (C; CA).

b) CA′ ⊥ BA′ tại A′ nên CA′ là tiếp tuyến của (B; BA).

CA ⊥ BA tại A nên CA là tiếp tuyến của (B; BA).

Vậy BA và BA′ là hai tiếp tuyến cắt nhau của (B; BA).

Bài 5.40

Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Một đường thẳng d đi qua A cắt (O) tại E và cắt (O') tại F (E và F) khác A. Biết điểm A nằm trong đoạn EF. Gọi I và K lần lượt là trung điểm của AE và AF (H.5.46).

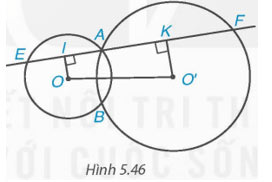
a) Chứng minh rằng tứ giác OO'KI là một hình thang vuông.

b) Chứng minh rằng IK=\(\frac{1}{2}\)EF.

c) Khi d ở vị trí nào (d vẫn qua A) thì OO'KI là một hình chữ nhật?