Toán 9 Luyện tập chung trang 18 Giải Toán 9 Kết nối tri thức tập 2 trang 18, 19, 20

Tải về Bình luận

Giải bài tập Toán 9 Luyện tập chung với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán 9 Tập 2 Kết nối tri thức trang 18, 19, 20. Qua đó, giúp các em ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán.

Giải Toán 9 chi tiết, đồng thời còn giúp các em hệ thống lại toàn bộ kiến thức trọng tâm của bài Luyện tập chung Chương VI: Hàm số y = ax² (a ≠ 0). Bên cạnh đó, cũng giúp thầy cô soạn giáo án cho học sinh của mình. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Eballsviet.com:

Toán 9 Luyện tập chung Kết nối tri thức

Giải Toán 9 Kết nối tri thức Tập 2 trang 19, 20

Giải Toán 9 Kết nối tri thức Tập 2 trang 19, 20

Bài 6.16 trang 19 Toán 9 Tập 2

Biết rằng parabol y = ax² (a ≠ 0) đi qua điểm $A\left( {2;4\sqrt 3 } \right)$ $A\left( {2;4\sqrt 3 } \right)$.

a) Tìm hệ số a và vẽ đồ thị của hàm số y = ax² với a vừa tìm được.

b) Tìm tung độ của điểm thuộc parabol có hoành độ x = – 1.

c) Tìm các điểm thuộc parabol có tung độ $y = 5\sqrt 3$ $y = 5\sqrt 3$.

Hướng dẫn giải:

a) Vì đồ thị của hàm số đi qua điểm $A\left( {2;4\sqrt 3 } \right)$ $A\left( {2;4\sqrt 3 } \right)$ nên:

$4\sqrt3\;=a.2^2$ $4\sqrt3\;=a.2^2$

$\Rightarrow a=\sqrt3$ $\Rightarrow a=\sqrt3$

Vậy hàm số cần tìm là: $y = \sqrt 3 {x^2}$ $y = \sqrt 3 {x^2}$.

Lập bảng một số cặp giá trị tương ứng của x và y:

x	– 2	– 1	0	1	2
y	$4\sqrt{3}$ $4\sqrt{3}$	$\sqrt{3}$ $\sqrt{3}$	0	$\sqrt{3}$ $\sqrt{3}$	$4\sqrt{3}$ $4\sqrt{3}$

Biểu diễn các điểm $\left( { - 2;4\sqrt 3 } \right);\left( { - 1;\sqrt 3 } \right);\left( {0;0} \right);\left( {1;\sqrt 3 } \right);\left( {2;4\sqrt 3 } \right)$ $\left( { - 2;4\sqrt 3 } \right);\left( { - 1;\sqrt 3 } \right);\left( {0;0} \right);\left( {1;\sqrt 3 } \right);\left( {2;4\sqrt 3 } \right)$ trên mặt phẳng tọa độ Oxy và nối chúng lại ta được đồ thị hàm số $y = \sqrt 3 {x^2}$ $y = \sqrt 3 {x^2}$ như hình vẽ.

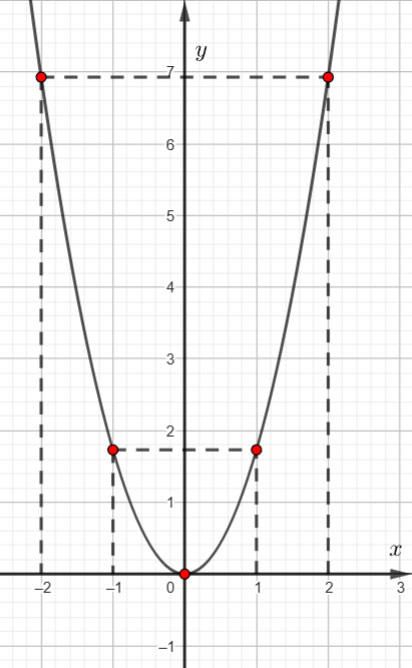
Luyện tập chung

b) Thay x = – 1 vào hàm số $y = \sqrt 3 {x^2}$ $y = \sqrt 3 {x^2}$ ta có:

$y = \sqrt 3 .{\left( { - 1} \right)^2} = \sqrt 3$ $y = \sqrt 3 .{\left( { - 1} \right)^2} = \sqrt 3$

Vậy tung độ của điểm thuộc parabol có hoành độ x = – 1 là $y = \sqrt 3$ $y = \sqrt 3$.

c) Ta có: $y = 5\sqrt 3$ $y = 5\sqrt 3$

⇒ $5\sqrt3\;=\sqrt3.x^2$ $5\sqrt3\;=\sqrt3.x^2$

⇒ $x = \sqrt 5$ $x = \sqrt 5$ hoặc $x=\;-\sqrt5$ $x=\;-\sqrt5$.

Vậy các điểm thuộc parabol có tung độ $y = 5\sqrt 3$ $y = 5\sqrt 3$ là $\left( {\sqrt 5 ;5\sqrt 3 } \right);\left( { - \sqrt 5 ;5\sqrt 3 } \right)$ $\left( {\sqrt 5 ;5\sqrt 3 } \right);\left( { - \sqrt 5 ;5\sqrt 3 } \right)$.

Bài 6.17 trang 20 Toán 9 Tập 2

Công thức $E = \frac{1}{2}m{v^2}\left( J \right)$ $E = \frac{1}{2}m{v^2}\left( J \right)$ được dùng để tính động năng của một vật có khối lượng m (kg) khi chuyển động với vận tốc v (m/s) (theo Vật lí đại cương, NXB Giáo dục Việt Nam, 2016).

a) Giả sử một quả bóng có khối lượng 2 kg đang bay với vận tốc 6 m/s. Tính động năng của quả bóng đó.

b) Giả sử động năng của quả bóng đang bay có khối lượng 1,5 kg là 48 J, hãy tính vận tốc bay của quả bóng đó.

Hướng dẫn giải:

a) Với m = 2, v = 6 động năng của quả bóng là:

$E = \frac{1}{2}{.2.6^2} = 36\left( J \right)$ $E = \frac{1}{2}{.2.6^2} = 36\left( J \right)$

b) Với E = 48 J và m = 1,5 nên ta có phương trình:

$48 = \frac{1}{2}.1,5.{v^2}$ $48 = \frac{1}{2}.1,5.{v^2}$

⇒ v² = 64

⇒ v = 8 (do v > 0)

Vậy vận tốc bay của quả bóng là 8 m/s.

Bài 6.18 trang 20 Toán 9 Tập 2

Cho hình chóp tam giác đều có đáy là tam giác đều cạnh a (cm) và chiều cao 10 cm.

a) Tính diện tích đáy S của hình chóp theo a.

b) Từ kết quả ở câu a, tính thể tích V của hình chóp theo a và tính giá trị của V khi a = 4 cm.

c) Nếu độ dài cạnh đáy giảm đi hai lần thì thể tích hình chóp thay đổi như thế nào?

Hướng dẫn giải:

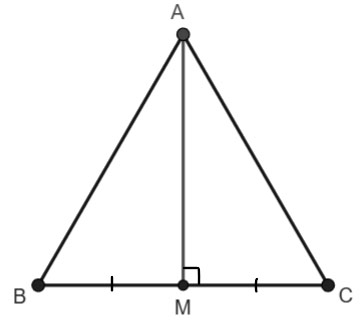
Luyện tập chung

Gọi A, B, C lần lượt là các đỉnh của đáy hình chóp tam giác đều

Khi đó AB = AC = BC = a và $\widehat{B}=60^{\circ}$ $\widehat{B}=60^{\circ}$

Kẻ AM ⊥ BC (M ∈ BC)

Xét tam giác ABM vuông tại M, ta có:

AM = AB . sin 60^o = $\frac{a\sqrt{3}}{2}$ $\frac{a\sqrt{3}}{2}$

Vậy diện tích đáy S của hình chóp là:

$S = \frac{1}{2}AM.BC= \frac{1}{2}.\frac{a\sqrt 3}{2}.a = \frac{a^2\sqrt 3}{4}$ $S = \frac{1}{2}AM.BC= \frac{1}{2}.\frac{a\sqrt 3}{2}.a = \frac{a^2\sqrt 3}{4}$ (cm²)

b) Thể tích V của hình chóp là:

$V = \frac{1}{3}S.h = \frac{1}{3}.\frac{a^2\sqrt 3}{4} . 10 = \frac{5\sqrt 3}{6} a^2$ $V = \frac{1}{3}S.h = \frac{1}{3}.\frac{a^2\sqrt 3}{4} . 10 = \frac{5\sqrt 3}{6} a^2$ (cm³)

Với a = 4 cm, thể tích hình chóp là:

$V = \frac{5\sqrt 3}{6}. 4^2=\frac{40\sqrt 3}{3}$ $V = \frac{5\sqrt 3}{6}. 4^2=\frac{40\sqrt 3}{3}$ (cm³)

c) Độ dài cạnh đáy sau khi thay đổi là $a'=\frac{a}{2}$

Khi đó thể tích hình chóp là:

$V = \frac{5a$ $V = \frac{5a'^2\sqrt 3}{6} =\frac{5\left (\frac{a}{2} ' \right ) ^2\sqrt 3}{6} =\frac{ 5.\frac{a}{4} ' .\sqrt 3}{6} =\frac{1}{4} V$

Vậy nếu độ dài cạnh đáy giảm đi hai lần thì thể tích hình chóp giảm đi 4 lần.

Bài 6.19 trang 20 Toán 9 Tập 2

Sử dụng công thức nghiệm hoặc công thức nghiệm thu gọn, giải các phương trình sau:

a) ${x^2} - 2\sqrt 5 x + 1 = 0$ ${x^2} - 2\sqrt 5 x + 1 = 0$

b) 3x² - 9x + 3 = 0

c) 11x² - 13x + 5 = 0

d) $2{x^2} + 2\sqrt 6 x + 3 = 0$ $2{x^2} + 2\sqrt 6 x + 3 = 0$

Hướng dẫn giải:

a) ${x^2} - 2\sqrt 5 x + 1 = 0$ ${x^2} - 2\sqrt 5 x + 1 = 0$

Ta có: ∆' = 5 - 1 = 4 > 0

Do đó phương trình có hai nghiệm phân biệt:

$x_1=\sqrt5\;+2;x_2=\sqrt5\;-2$ $x_1=\sqrt5\;+2;x_2=\sqrt5\;-2$

b) 3x² - 9x + 3 = 0

Ta có: ∆ = (- 9)² - 4 . 3 . 3 = 45 > 0

Do đó phương trình có hai nghiệm phân biệt:

${x_1} = \frac{{3 + \sqrt 5 }}{2};{x_2} = \frac{{3 - \sqrt 5 }}{2}$ ${x_1} = \frac{{3 + \sqrt 5 }}{2};{x_2} = \frac{{3 - \sqrt 5 }}{2}$

c) 11x² - 13x + 5 = 0

Ta có: ∆ = (- 13)² - 4 . 11 . 5 = - 51 < 0

Do đó phương trình vô nghiệm.

d) $2{x^2} + 2\sqrt 6 x + 3 = 0$ $2{x^2} + 2\sqrt 6 x + 3 = 0$

Ta có: ∆' = 6 - 2 . 3 = 0

Do đó phương trình có nghiệm kép ${x_1} = {x_2} = \frac{{ - \sqrt 6 }}{2}$ ${x_1} = {x_2} = \frac{{ - \sqrt 6 }}{2}$.

Bài 6.20 trang 20 Toán 9 Tập 2

Sử dụng máy tính cầm tay, tìm nghiệm gần đúng của các phương trình sau (làm tròn kết quả đến chữ số thập phân thứ hai):

a) $\sqrt{2}x^2-\sqrt{5}x-1=0$ $\sqrt{2}x^2-\sqrt{5}x-1=0$

b) $x^2-\left(\sqrt{3}-1\right)x-\sqrt{7}=0$ $x^2-\left(\sqrt{3}-1\right)x-\sqrt{7}=0$

Hướng dẫn giải:

a) $\sqrt{2}x^2-\sqrt{5}x-1=0$ $\sqrt{2}x^2-\sqrt{5}x-1=0$

Phương trình có hai nghiệm phân biệt x₁ ≈ 1,94, x₂ ≈ - 0,36

b) $x^2-\left(\sqrt{3}-1\right)x-\sqrt{7}=0$ $x^2-\left(\sqrt{3}-1\right)x-\sqrt{7}=0$

Phương trình có hai nghiệm phân biệt x₁ ≈ 2,03, x₂ ≈ - 1,3.

Bài 6.21 trang 20 Toán 9 Tập 2

Từ một tấm tôn hình vuông, người ta cắt bỏ bốn hình vuông có độ dài cạnh 8 cm ở bốn góc, sau đó gập thành một chiếc thùng có dạng hình hộp chữ nhật không có nắp và có thể tích là 200 cm³. Tính độ dài cạnh của tấm tôn hình vuông ban đầu.

Hướng dẫn giải:

Gọi x (cm) là độ dài cạnh của tấm tôn ban đầu (x > 16)

Sau khi cắt bỏ bốn hình vuông có độ dài cạnh 8 cm ở bốn góc, ta có các kích thước của chiếc thùng có dạng hình hộp chữ nhật là:

⦁ 2 cạnh đáy đều là: x – 8 . 2 = x – 16 (cm)

⦁ chiều cao là: 8 (cm)

Thể tích hình hộp chữ nhật: 8(x – 16)² (cm³).

Vì thể tích của hộp là 200 cm³ nên ta có phương trình:

8(x – 16)² = 200

⇒ (x – 16)² = 25

⇒ x – 16 = 5 hoặc x – 16 = –5

⇒ x = 21 (tm) hoặc x = 11 (loại)

Vậy độ dài cạnh của tấm tôn ban đầu là 21 cm.

Bài 6.22 trang 20 Toán 9 Tập 2

Giả sử doanh thu (nghìn đồng) của một cửa hàng bán phở trong một ngày có thể mô hình hoá bằng công thức R(x) = x(220 – 4x) với 30 ≤ x ≤ 50, trong đó x (nghìn đồng) là giá tiền của một bát phở. Nếu muốn doanh thu của cửa hàng đạt 3 triệu đồng thì giá bán của mỗi bát phở phải là bao nhiêu?

Chia sẻ bởi: