Toán 9 Bài 1: Phương trình quy về phương trình bậc nhất một ẩn Giải Toán 9 Cánh diều tập 1 trang 5, 6, 7, 8, 9, 10, 11

Giải bài tập Toán 9 Bài 1: Phương trình quy về phương trình bậc nhất một ẩn với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán 9 Tập 1 Cánh diều trang 5, 6, 7, 8, 9, 10, 11.. Qua đó, giúp các em ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán.

Giải Toán 9 Bài 1 chi tiết phần luyện tập, bài tập, đồng thời còn giúp các em hệ thống lại toàn bộ kiến thức trọng tâm của Bài 1 Chương I: Phương tình và hệ phương trình bậc nhất. Bên cạnh đó, cũng giúp thầy cô soạn giáo án cho học sinh của mình. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Eballsviet.com:

Phần Luyện tập

Luyện tập 1 trang 6 Toán 9 tập 1

Giải phương trình: (4x + 5)(3x - 2) = 0.

Lời giải:

Để giải phương trình đã cho, ta giải hai phương trình sau:

Vậy phương trình đã cho có hai nghiệm là \(x=-\frac{5}{4}\) và \(x=\frac{2}{3}\).

Luyện tập 2 trang 7 Toán 9 tập 1

Giải các phương trình:

a) x² - 10x + 25 = 5(x - 5)

b) 4x² - 16 = 5(x + 2).

Lời giải:

a) Ta có: x² - 10x + 25 = 5(x - 5)

(x - 5)² - 5(x - 5) = 0

(x - 5)(x - 10) = 0

Để giải phương trình đã cho, ta giải hai phương trình sau:

Vậy phương trình đã cho có hai nghiệm là x = 5 và x = 10.

b) Ta có: 4x² - 16 = 5(x + 2).

4(x² - 4) = 5(x + 2)

4(x + 2)(x - 2) - 5(x + 2) = 0

(x + 2)(4x - 13) = 0

Để giải phương trình đã cho, ta giải hai phương trình sau:

Vậy phương trình đã cho có hai nghiệm là x = - 2 và \(x=\frac{13}{4}\).

Luyện tập 3 trang 8 Toán 9 tập 1

Tìm điều kiện xác định của phương trình sau:

\(\frac{x-8}{x-7}=8+\frac{1}{1-x}\)

Lời giải:

Điều kiện xác định của phương trình \(\frac{x-8}{x-7}=8+\frac{1}{1-x}\) là:

x - 7 ≠ 0 và 1 - x ≠ 0 hay x ≠ 7 và x ≠ 1.

Luyện tập 4 trang 9 Toán 9 tập 1

Giải phương trình:

\(\frac{x}{x-2}+\frac{1}{x-3}=\frac{2}{\left(2-x\right)\left(x-3\right)}\)

Lời giải:

Điều kiện xác định: x ≠ 2 và x ≠ 3.

\(\frac{x}{x-2}+\frac{1}{x-3}=\frac{2}{\left(2-x\right)\left(x-3\right)}\)

\(\frac{x\left(x-3\right)}{\left(x-2\right)\left(x-3\right)}+\frac{x-2}{\left(x-2\right)\left(x-3\right)}=\frac{-2}{\left(x-2\right)\left(x-3\right)}\)

x(x + 3) + x - 2 = - 2

x² + 3x + x - 2 + 2 = 0

x² + 4x = 0

x(x + 4) = 0

x = 0 hoặc x = - 4 (tmđk)

Vậy phương trình đã cho có hai nghiệm là x = 0 và x = - 4.

Luyện tập 5 trang 10 Toán 9 tập 1

Một đội công nhân làm đường nhận nhiệm vụ trải nhựa 8100 m ² mặt đường. Ở giai đoạn đầu, đội trải được 3 600 m ² mặt đường. Ở giai đoạn sau, đội công nhân tăng năng suất thêm 300 m ² /ngày rồi hoàn thành công việc. Hỏi đội công nhân đã hoàn thành công việc trong bao nhiêu ngày? Biết rằng thời gian làm việc của hai giai đoạn là như nhau và năng suất lao động của đội trong từng giai đoạn là không thay đổi.

Lời giải:

Gọi số ngày đội công nhân hoàn thành công việc là x (ngày) (x > 0)

Số ngày làm việc ở mỗi giai đoạn là: \(\frac{x}{2}\) (ngày)

Năng suất của đội trong giai đoạn đầu là: \(\frac{3600}{\frac{x}{2}}=\frac{7200}{x}\) (m²/ngày)

Năng suất của đội trong giai đoạn sau là: \(\frac{8100-3600}{\frac{x}{2}}=\frac{9000}{x}\) (m²/ngày)

Do ở giai đoạn sau, đội công nhân tăng năng suất thêm 300 m²/ngày nên ta có phương trình:

\(\frac{9000}{x}-\frac{7200}{x}=300\)

\(\frac{1800}{x}=300\)

x = 6 (tmđk)

Vậy đội công nhân đã hoàn thành công việc trong 6 ngày.

Phần Bài tập

Bài 1 trang 11 Toán 9 tập 1

Giải các phương trình:

a) (9x – 4)(2x + 5) = 0;

b) (1,3x + 0,26)(0,2x – 4) = 0;

c) 2x(x + 3) – 5(x + 3) = 0;

d) x² – 4 + (x + 2)(2x – 1) = 0.

Lời giải:

a) Để giải được phương trình (9x – 4)(2x + 5) = 0, ta giải hai phương trình sau:

Vậy phương trình đã cho có hai nghiệm là x= \(\frac{4}{9}\) và x=\(\frac{-5}{2}\)

b) Để giải được phương trình (1,3x + 0,26)(0,2x – 4) = 0, ta giải hai phương trình sau:

Vậy phương trình đã cho có hai nghiệm là x = –0,2 và x = 20.

c) 2x(x + 3) – 5(x + 3) = 0

(x + 3)(2x – 5) = 0.

Để giải được phương trình (x + 3)(2x – 5) = 0, ta giải hai phương trình sau:

Vậy phương trình đã cho có hai nghiệm là x = –3 và x=\(\frac{5}{2}\)

d) x² – 4 + (x + 2)(2x – 1) = 0

(x – 2)(x + 2) + (x + 2)(2x – 1) = 0

(x + 2)(x – 2 + 2x – 1) = 0

(x + 2)(3x – 3) = 0.

Để giải được phương trình (x + 2)(3x – 3) = 0, ta giải hai phương trình sau:

Vậy phương trình đã cho có hai nghiệm là x = –2 và x = 1.

Bài 2 trang 11 Toán 9 tập 1

Giải các phương trình:

a) \(\frac{1}{x}=\frac{5}{3\left(x+2\right)}\)

b) \(\frac{x}{2x-1}=\frac{x-2}{2x+5}\)

c) \(\frac{5x}{x-2}=7+\frac{10}{x-2}\)

d) \(\frac{x^2-6}{x}=x+\frac{3}{2}\)

Lời giải:

a) Điều kiện xác định của phương trình: x ≠ 0 và x ≠ - 2.

\(\frac{1}{x}=\frac{5}{3\left(x+2\right)}\)

\(\frac{3\left(x+2\right)}{3x\left(x+2\right)}=\frac{5x}{3x\left(x+2\right)}\)

3(x + 2) = 5x

3x + 6 = 5x

2x = 6

x = 3

Ta thấy x = 3 thỏa mãn điều kiện xác định của phương trình.

Vậy phương trình đã cho có nghiệm là x = 3.

b) Điều kiện xác định của phương trình: x ≠ \(\frac{1}{2}\) và x ≠ \(-\frac{5}{2}\).

\(\frac{x}{2x-1}=\frac{x-2}{2x+5}\)

\(\frac{x\left(2x+5\right)}{\left(2x-1\right)\left(2x+5\right)}=\frac{\left(x-2\right)\left(2x-1\right)}{\left(2x-1\right)\left(2x+5\right)}\)

x(2x + 5) = (x - 2)(2x - 1)

2x² + 5x = 2x² + 10x - 2x - 5

3x = 5

\(x=\frac{5}{3}\)

Ta thấy \(x=\frac{5}{3}\) thỏa mãn điều kiện xác định của phương trình.

Vậy phương trình đã cho có nghiệm là \(x=\frac{5}{3}\).

c) Điều kiện xác định của phương trình: x ≠ 2.

\(\frac{5x}{x-2}=7+\frac{10}{x-2}\)

\(\frac{5x}{x-2}=\frac{7\left(x-2\right)}{x-2}+\frac{10}{x-2}\)

5x = 7x - 14 + 10

2x = 4

x = 2

Ta thấy x = 2 thỏa mãn điều kiện xác định của phương trình.

Vậy phương trình đã cho có hai nghiệm là x = 2.

d) Điều kiện xác định của phương trình: x ≠ 0.

\(\frac{x^2-6}{x}=x+\frac{3}{2}\)

\(\frac{2\left(x^2-6\right)}{2x}=\frac{2x^2}{2x}+\frac{3x}{2x}\)

2(x² - 6) = 2x² + 3x

2x² - 12 = 2x² + 3x

3x = - 12

x = - 4

Ta thấy x = - 4 thỏa mãn điều kiện xác định của phương trình.

Vậy phương trình đã cho có hai nghiệm là x = - 4.

Bài 3 trang 11 Toán 9 tập 1

Một ca nô đi xuôi dòng từ địa điểm A đến địa điểm B, rồi lại đi ngược dòng từ địa điểm B trở về địa điểm A. Thời gian cả đi và về là 3 giờ. Tính tốc độ của dòng nước. Biết tốc độ của ca nô khi nước yên lặng là 27km/h và độ dài quãng đường AB là 40km.

Lời giải:

Gọi tốc độ của dòng nước là: \(x\) (km/h, 0 < x < 27)

Vận tốc cano khi xuôi dòng là:\(27 + x\) (km/h);

Vận tốc cano khi ngược dòng là: \(27 - x\) (km/h);

Thời gian cano khi xuôi dòng là: \(\frac{{40}}{{27 + x}}\) (giờ);

Thời gian cano khi ngược dòng là: \(\frac{{40}}{{27 - x}}\) (giờ).

Do thời gian cả đi và về là 3 giờ nên ta có phương trình:

\(\frac{{40}}{{27 + x}} + \frac{{40}}{{27 - x}} = 3\)

\(\frac{{40\left( {27 - x} \right)}}{{\left( {27 + x} \right)\left( {27 - x} \right)}} + \frac{{40\left( {27 + x} \right)}}{{\left( {27 + x} \right)\left( {27 - x} \right)}} = \frac{{3\left( {27 + x} \right)\left( {27 - x} \right)}}{{\left( {27 + x} \right)\left( {27 - x} \right)}}\)

\(1080 - 40x + 1080 + 40x = 3\left( {729 - {x^2}} \right)\)

\(2160 = 2187 - 3{x^2}\)

\(3{x^2} - 27 = 0\)

\(3{x^2} = 27\)

\({x^2} = 9\)

\(x = 3\) (Thỏa mãn điều kiện).

Vậy tốc độ của dòng nước là 3 (km/h).

Bài 4 trang 11 Toán 9 tập 1

Một doanh nghiệp sử dụng than để sản xuất sản phẩm. Doanh nghiệp đó lập kế hoạch tài chính cho việc loại bỏ chất ô nhiễm khí thải theo dự kiến sau: Để loại bỏ \(p\%\) chất ô nhiễm trong khí thải thì chi phí \(C\) (Triệu đồng) được tính theo công thức: \(C = \frac{{80}}{{100 - p}}\) với \(0 \le p < 100\). Với chi phí là 420 triệu đồng thì doanh nghiệp loại bỏ được bao nhiêu phần trăm chất gây ô nhiễm trong khí thải (làm tròn kết quả đến hàng phần mười)?

Lời giải:

Với chi phí là 420 triệu đồng ta có: \(420 = \frac{{80}}{{100 - p}}\)

\(4200 - 420p = 80\)

\(420p = 4120\)

\(p \approx 9,8\).

Vậy với chi phí là 420 triệu đồng thì doanh nghiệp loại bỏ được 9,8% chất gây ô nhiễm trong khí thải.

Bài 5 trang 11 Toán 9 tập 1

Bạn Hoa dự định dùng hết số tiền 600 nghìn đồng để mua một số chiếc áo đồng giá tặng các bạn có hoàn cảnh khó khăn. Khi đến cửa hàng, loại áo mà bạn Hoa dự định mua được giảm giá 30 nghìn đồng/chiếc. Do vậy, bạn Hoa đã mua được số lượng áo gấp 1,25 lần so với số lượng dự định. Tính giá tiền của mỗi chiếc áo bạn Hoa đã mua.

Lời giải:

Gọi giá tiền của mỗi chiếc áo bạn Hoa đã mua là \(x\) (nghìn đồng, \(0 < x < 600\)).

Giá tiền của mỗi chiếc áo bạn Hoa dự định mua là: \(x - 30\) (nghìn đồng)

Số lượng áo bạn Hoa đã mua là: \(\frac{{600}}{x}\) (chiếc)

Số lượng áo bạn Hoa dự định mua là: \(\frac{{600}}{{x - 30}}\) (chiếc)

Do bạn Hoa đã mua được số lượng áo gấp 1,25 lần so với số lượng dự định nên ta có phương trình:

\(1,25.\frac{{600}}{x} = \frac{{600}}{{x - 30}}\)

\(\frac{{750\left( {x - 30} \right)}}{{x\left( {x - 30} \right)}} = \frac{{600x}}{{x\left( {x - 30} \right)}}\)

\(750x - 22500 = 600x\)

\(750x - 600x = 22500\)

\(150x = 22500\)

\(x = 150\)(Thoả mãn điều kiện).

Vậy giá tiền mỗi chiếc áo bạn Hoa đã mua là 150 nghìn đồng.

Bài 6 trang 11 Toán 9 tập 1

Một mảnh đất có dạng hình chữ nhật với chu vi bằng 52 m. Trên mảnh đất đó, người ta làm một vườn rau có dạng hình chữ nhật với diện tích là 112 m² và một lối đi xung quanh vườn rộng 1 m (Hình 2). Tính các kích thước của mảnh đất đó.

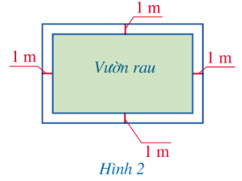
Lời giải:

Nửa chu vi của mảng đất hình chữ nhật là 52 : 2 = 26 (m).

Gọi chiều rộng của mảnh đất hình chữ nhật là x (m) (x < 13).

Khi đó, chiều dài của mảnh đất hình chữ nhật là 26 – x (m).

Chiều rộng của vườn rau là x – 1 – 1 = x – 2 (m).

Chiều dài của vườn rau là 26 – x – 1 – 1 = 24 – x (m).

Diện tích của vườn rau là (x – 2)(24 – x) (m2).

Theo bài, vườn rau có dạng hình chữ nhật với diện tích là 112 m² nên ta có phương trình: (x – 2)(24 – x) = 112.

Giải phương trình:

(x – 2)(24 – x) = 112

24x – x2 – 48 + 2x – 112 = 0

– x² + 26x – 160 = 0

x² – 26x + 160 = 0

x² – 10x – 16x + 160 = 0

(x² – 10x) – (16x – 160) = 0

x(x – 10) – 16(x – 10) = 0

(x – 10)(x – 16) = 0

x – 10 = 0 hoặc x – 16 = 0

x = 10 hoặc x = 16.

Do x < 13 nên x = 10.

Vậy mảnh đất có chiều rộng là 10 m và chiều dài là 26 – 10 = 16 m.