Toán 9 Bài 3: Căn thức bậc hai và căn thức bậc ba của biểu thức đại số Giải Toán 9 Cánh diều tập 1 trang 61, 62, 63, 64, 65, 66

Tải về Bình luận

Bài trước

Mục lục

Bài sau

Giải Toán 9 Bài 3: Căn thức bậc hai và căn thức bậc ba của biểu thức đại số là tài liệu vô cùng hữu ích giúp các em học sinh lớp 9 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 9 Cánh diều tập 1 trang 61, 62, 63, 64, 65, 66.

Giải bài tập Toán 9 Cánh diều tập 1 Bài 3 - Chương III: Căn thức được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh học tập. Vậy mời thầy cô và các em theo dõi bài viết dưới đây của Eballsviet.com:

Toán 9 Bài 3: Căn thức bậc hai và căn thức bậc ba của biểu thức đại số Cánh diều

Giải Toán 9 Cánh diều Tập 1 trang 65, 66
- Bài 1
- Bài 2
- Bài 3
- Bài 4
- Bài 5
- Bài 7

Giải Toán 9 Cánh diều Tập 1 trang 65, 66

Bài 1

Tính giá trị của mỗi căn thức bậc hai sau:

a. $\sqrt[{}]{{17 - {x^2}}}$ $\sqrt[{}]{{17 - {x^2}}}$ tại x = 1; x = - 3; x = $2\sqrt[{}]{2};$ $2\sqrt[{}]{2};$

b. $\sqrt[{}]{{{x^2} + x + 1}}$ $\sqrt[{}]{{{x^2} + x + 1}}$ tại x = 0;x = - 1; x = - 7.

Hướng dẫn giải:

a. Thay x = 1 vào biểu thức, ta được: $\sqrt {17 - {1^2}} = \sqrt {17 - 1} = \sqrt {16} = 4.$ $\sqrt {17 - {1^2}} = \sqrt {17 - 1} = \sqrt {16} = 4.$

Thay x = - 3 vào biểu thức, ta được: $\sqrt {17 - {{\left( { - 3} \right)}^2}} = \sqrt {17 - 9} = \sqrt 8 .$ $\sqrt {17 - {{\left( { - 3} \right)}^2}} = \sqrt {17 - 9} = \sqrt 8 .$

Thay $x = 2\sqrt 2$ $x = 2\sqrt 2$ vào biểu thức, ta được: $\sqrt {17 - {{\left( {2\sqrt 2 } \right)}^2}} = \sqrt {17 - 8} = \sqrt 9 = 3.$ $\sqrt {17 - {{\left( {2\sqrt 2 } \right)}^2}} = \sqrt {17 - 8} = \sqrt 9 = 3.$

b. Thay x = 0 vào biểu thức, ta được: $\sqrt {{0^2} + 0 + 1} = \sqrt 1 = 1.$ $\sqrt {{0^2} + 0 + 1} = \sqrt 1 = 1.$

Thay x = - 1 vào biểu thức, ta được: $\sqrt {{{\left( { - 1} \right)}^2} + \left( { - 1} \right) + 1} = \sqrt 1 = 1.$ $\sqrt {{{\left( { - 1} \right)}^2} + \left( { - 1} \right) + 1} = \sqrt 1 = 1.$

Thay x = - 7 vào biểu thức, ta được: $\sqrt {{{\left( { - 7} \right)}^2} + \left( { - 7} \right) + 1} = \sqrt {49 - 7 + 1} = \sqrt {43} .$ $\sqrt {{{\left( { - 7} \right)}^2} + \left( { - 7} \right) + 1} = \sqrt {49 - 7 + 1} = \sqrt {43} .$

Bài 2

Tìm điều kiện xác định cho mỗi căn thức bậc hai sau:

a. $\sqrt[{}]{{x - 6}}$ $\sqrt[{}]{{x - 6}}$

b. $\sqrt[{}]{{17 - x}}$ $\sqrt[{}]{{17 - x}}$

c. $\sqrt[{}]{{\frac{1}{x}}}$ $\sqrt[{}]{{\frac{1}{x}}}$

Hướng dẫn giải:

a. $\sqrt {x - 6}$ $\sqrt {x - 6}$xác định khi $x - 6 \ge 0$ $x - 6 \ge 0$ hay $x \ge 6.$ $x \ge 6.$

b. $\sqrt {17 - x}$ $\sqrt {17 - x}$ xác định khi 1 $7 - x \ge 0$ $7 - x \ge 0$ hay $x \le 17.$ $x \le 17.$

c. $\sqrt {\frac{1}{x}}$ $\sqrt {\frac{1}{x}}$xác định khi $\frac{1}{x} \ge 0$ $\frac{1}{x} \ge 0$ và $x \ne 0$ $x \ne 0$ hay x > 0.

Bài 3

Tính giá trị của mỗi căn thức bậc ba sau:

a. $\sqrt[3]{{2x - 7}}$ $\sqrt[3]{{2x - 7}}$ tại x = - 10; x = 7,5; x = - 0,5

b. $\sqrt[3]{{{x^2} + 4}}$ $\sqrt[3]{{{x^2} + 4}}$ tại x = 0; x = 2 ; $x = \sqrt[{}]{{23}}.$ $x = \sqrt[{}]{{23}}.$

Hướng dẫn giải:

a. Thay x = - 10 vào biểu thức, ta được:

Thay x = 7,5 vào biểu thức, ta được: $\sqrt[3]{{2.7,5 - 7}} = \sqrt[3]{{15 - 7}} = \sqrt[3]{8} = 2.$ $\sqrt[3]{{2.7,5 - 7}} = \sqrt[3]{{15 - 7}} = \sqrt[3]{8} = 2.$

Thay x = - 0,5 vào biểu thức, ta được: $\sqrt[3]{{2.\left( { - 0,5} \right) - 7}} = \sqrt[3]{{ - 1 - 7}} = \sqrt[3]{{ - 8}} = - 2.$ $\sqrt[3]{{2.\left( { - 0,5} \right) - 7}} = \sqrt[3]{{ - 1 - 7}} = \sqrt[3]{{ - 8}} = - 2.$

b. Thay x = 0 vào biểu thức, ta được: $\sqrt[3]{{{0^2} + 4}} = \sqrt[3]{4}.$ $\sqrt[3]{{{0^2} + 4}} = \sqrt[3]{4}.$

Thay x = 2 vào biểu thức, ta được: $\sqrt[3]{{{2^2} + 4}} = \sqrt[3]{{4 + 4}} = \sqrt[3]{8} = 2.$ $\sqrt[3]{{{2^2} + 4}} = \sqrt[3]{{4 + 4}} = \sqrt[3]{8} = 2.$

Thay $x = \sqrt[{}]{{23}}$ $x = \sqrt[{}]{{23}}$ vào biểu thức, ta được: $\sqrt[3]{{{{\left( {\sqrt[{}]{{23}}} \right)}^2} + 4}} = \sqrt[3]{{23 + 4}} = \sqrt[3]{{27}} = 3.$ $\sqrt[3]{{{{\left( {\sqrt[{}]{{23}}} \right)}^2} + 4}} = \sqrt[3]{{23 + 4}} = \sqrt[3]{{27}} = 3.$

Bài 4

Tìm điều kiện xác định cho mỗi căn thức bậc ba sau:

a. $\sqrt[3]{{3x + 2}}$ $\sqrt[3]{{3x + 2}}$

b. $\sqrt[3]{{{x^3} - 1}}$ $\sqrt[3]{{{x^3} - 1}}$

c. $\sqrt[3]{{\frac{1}{{2 - x}}}}$ $\sqrt[3]{{\frac{1}{{2 - x}}}}$

Hướng dẫn giải:

a. $\sqrt[3]{{3x + 2}}$ $\sqrt[3]{{3x + 2}}$ xác định với mọi số thực x vì 3x + 2 xác định với mọi số thực x.

b. $\sqrt[3]{{{x^3} - 1}}$ $\sqrt[3]{{{x^3} - 1}}$ xác định với mọi số thực x vì ${x^3}$ ${x^3}$ - 1 xác định với mọi số thực x.

c. $\sqrt[3]{{\frac{1}{{2 - x}}}}$ $\sqrt[3]{{\frac{1}{{2 - x}}}}$ xác định với $x \ne 2$ $x \ne 2$ vì $\frac{1}{{2 - x}}$ $\frac{1}{{2 - x}}$ xác định với x \ne 2.

Bài 5

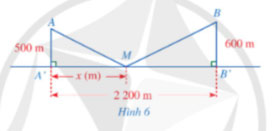
Có hai xã A, B cùng ở một bên bờ sông Lam, khoảng cách từ hai xác đó đến bờ sông lần lượt là AA' = 500m,BB' = 600m và người ta đo dược A'B' = 2200m. Các kĩ sư muốn xây một trạm cung cấp nước sạch nằm bên bờ sông Lam cho người dân hai xã. Giả sử vị trí của trạm cung cấp nước sạch đó là điểm M trên đoạn A'B' với MA' = x\left( m \right), 0 < x < 2200 (minh họa ở Hình 6).

a. Hãy tính tổng khoảng cách MA + MB theo x.

b. Tính tổng khoảng cách MA + MB khi x = 1200 (làm tròn kết quả đến hàng đơn vị của mét).

Hình 6

Hướng dẫn giải:

a. Ta có: MB = 2200 - x

Áp dụng định lý Py – ta – go vào tam giác MAA’ ta có:

$\begin{array}{l}M{A^2} = MA{$ $\begin{array}{l}M{A^2} = MA{'^2} + AA{'^2}\\M{A^2} = {x^2} + {500^2}\\MA = \sqrt {{x^2} + {{500}^2}} \end{array}$

Áp dụng định lý Py – ta – go vào tam giác MBB' ta có:

$\begin{array}{l}M{B^2} = BB{$ $\begin{array}{l}M{B^2} = BB{'^2} + MB{'^2} \Rightarrow M{B^2} = {600^2} + {\left( {2200 - x} \right)^2}\\M{B^2} = 360000 + 4840000 - 4400x + {x^2} = 5200000 - 4400x + {x^2}\\MB = \sqrt {5200000 - 4400x + {x^2}} \end{array}$

Vậy $MA + MB = \sqrt {{x^2} + {{500}^2}} + \sqrt {5200000 - 4400x + {x^2}} .$ $MA + MB = \sqrt {{x^2} + {{500}^2}} + \sqrt {5200000 - 4400x + {x^2}} .$

b. Thay x = 1200vào biểu thức tính MA + MB, ta được:

$\begin{array}{l}MA + MB = \sqrt {{{1200}^2} + {{500}^2}} + \sqrt {5200000 - 4400.1200 + {{1200}^2}} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \sqrt {1440000 + 250000} + \sqrt {5200000 - 5280000 + 1440000} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \sqrt {1690000} + \sqrt {1360000} \\MA + MB \approx 2466\left( {cm} \right) \approx 24\left( m \right).\end{array}$ $\begin{array}{l}MA + MB = \sqrt {{{1200}^2} + {{500}^2}} + \sqrt {5200000 - 4400.1200 + {{1200}^2}} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \sqrt {1440000 + 250000} + \sqrt {5200000 - 5280000 + 1440000} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \sqrt {1690000} + \sqrt {1360000} \\MA + MB \approx 2466\left( {cm} \right) \approx 24\left( m \right).\end{array}$

Bài 7

Chiều cao ngang vai của một con voi đực ở châu Phi là h (cm) có thể được tính xấp xỉ bằng công thức: $h = 62,5.\sqrt[3]{t} + 75,8$ $h = 62,5.\sqrt[3]{t} + 75,8$ với t là tuổi của con voi tính theo năm.

a. Một con voi đực 8 tuổi có chiều cao ngang vai là bao nhiêu centimét?

b. Nếu một con voi đực có chiều cao ngang vai là 205cm thì con voi đó bao nhiêu tuổi (làm tròn kết quả đến hàng đơn vị)?

Hướng dẫn giải:

a. Một con voi đực 8 tuổi thì có chiều cao ngang vai là:

$h = 62,5.\sqrt[3]{8} + 75,8 = 62,5.2 + 75,8 = 200,8\left( {cm} \right)$ $h = 62,5.\sqrt[3]{8} + 75,8 = 62,5.2 + 75,8 = 200,8\left( {cm} \right)$

b. Nếu một con voi đực có chiều cao ngang vai là 205cm thì con voi đó số tuổi là:

$\begin{array}{l}205 = 62,5\sqrt[3]{t} + 75,8\\\sqrt[3]{t} = 2,0672\\t \approx 9\end{array}$ $\begin{array}{l}205 = 62,5\sqrt[3]{t} + 75,8\\\sqrt[3]{t} = 2,0672\\t \approx 9\end{array}$

Vậy nếu một con voi đực có chiều cao ngang vai là 205cm thì con voi đó 9 tuổi.

Chia sẻ bởi: