Toán 9 Bài 2: Phương trình bậc nhất hai ẩn. Hệ hai phương trình bậc nhất hai ẩn Giải Toán 9 Cánh diều tập 1 trang 12, 13, 14, 15, 16, 17, 18

Giải Toán 9 Bài 2: Phương trình bậc nhất hai ẩn, Hệ hai phương trình bậc nhất hai ẩn là tài liệu vô cùng hữu ích giúp các em học sinh lớp 9 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 9 Cánh diều tập 1 trang 12, 13, 14, 15, 16, 17, 18.

Giải bài tập Toán 9 Cánh diều tập 1 Bài 2 - Chương I: Phương tình và hệ phương trình bậc nhất được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh học tập. Vậy mời thầy cô và các em theo dõi bài viết dưới đây của Eballsviet.com:

Giải Toán 9 Cánh diều Tập 1 trang 17, 18

Bài 1

Trong các cặp số (8; 1), (–3; 6), (4; –1), (0; 2), cho biết cặp số nào là nghiệm của mỗi phương trình sau:

a) x – 2y = 6;

b) x + y = 3.

Lời giải:

a) ⦁ Thay x = 8 và y = 1 vào vế trái của phương trình x – 2y = 6, ta có:

8 – 2.1 = 8 – 2 = 6.

Do đó cặp số (8; 1) là nghiệm của phương trình x – 2y = 6.

⦁ Thay x = –3 và y = 6 vào vế trái của phương trình x – 2y = 6, ta có:

–3 – 2.6 = –3 – 12 = –15 ≠ 6.

Do đó cặp số (–3; 6) không là nghiệm của phương trình x – 2y = 6.

⦁ Thay x = 4 và y = –1 vào vế trái của phương trình x – 2y = 6, ta có:

4 – 2.(–1) = 4 + 2 = 6.

Do đó cặp số (4; –1) là nghiệm của phương trình x – 2y = 6.

⦁ Thay x = 0 và y =2 vào vế trái của phương trình x – 2y = 6, ta có:

0 – 2.2 = 0 + 4 = 4 ≠ 6.

Do đó cặp số (0; 2) không là nghiệm của phương trình x – 2y = 6.

Vậy các cặp số (8; 1) và (4; –1) là nghiệm của phương trình x – 2y = 6.

b) ⦁ Thay x = 8 và y = 1 vào vế trái của phương trình x + y = 3, ta có:

8 + 1 = 9 ≠ 3.

Do đó cặp số (8; 1) không là nghiệm của phương trình x + y = 3.

⦁ Thay x = –3 và y = 6 vào vế trái của phương trình x + y = 3, ta có:

–3 + 6 = 3.

Do đó cặp số (–3; 6) là nghiệm của phương trình x + y = 3.

⦁ Thay x = 4 và y = –1 vào vế trái của phương trình x + y = 3, ta có:

4 + (–1) = 3.

Do đó cặp số (4; –1) là nghiệm của phương trình x + y = 3.

⦁ Thay x = 0 và y =2 vào vế trái của phương trình x + y = 3, ta có:

0 + 2 = 2 ≠ 3.

Do đó cặp số (0; 2) không là nghiệm của phương trình x + y = 3.

Vậy các cặp số (–3; 6) và (4; –1) là nghiệm của phương trình x + y = 3.

Bài 2

Cho hệ phương trình:

\(\left\{ \begin{array}{l}x + 2y = 1\\3x - 2y = 3;\end{array} \right.\)

Trong các cặp số sau, cặp số nào là nghiệm của hệ phương trình đã cho?

a) (3; –1).

b) (1; 0).

Lời giải:

a) Thay x = 3 và y = –1 vào mỗi phương trình trong hệ, ta có:

3 + 2.(–1) = 1;

3.3 – 2.(–1) = 11 ≠ 3.

Do đó, cặp số (3; –1) không là nghiệm của phương trình thứ hai trong hệ.

Vậy cặp số (3; –1) không là nghiệm của hệ phương trình đã cho.

b) Thay x = 1 và y = 0 vào mỗi phương trình trong hệ, ta có:

1 + 2.0 = 1;

3.1 – 2.0 = 3.

Do đó, cặp số (1; 0) là nghiệm của từng phương trình trong hệ.

Vậy cặp số (1; 0) là nghiệm của hệ phương trình đã cho.

Bài 3

Nhân dịp tết Trung thu, một doanh nghiệp dự định sản xuất hai loại bánh: bánh nướng và bánh dẻo. Lượng đường cần cho mỗi chiếc bánh nướng, bánh dẻo lần lượt là 60 g, 50 g. Gọi x và y lần lượt là số lượng bánh nướng và bánh dẻo mà doanh nghiệp dự định sản xuất để lượng đường sản xuất bánh là 500 kg. Viết phương trình bậc nhất hai ẩn x, y biểu thị lượng đường để sản xuất hai loại bánh và chỉ ra ba nghiệm của phương trình đó.

Lời giải:

Lượng đường trong x chiếc bánh nướng là 60x (g).

Lượng đường trong y chiếc bánh dẻo là 50y (g).

Khi đó, lượng đường trong x chiếc bánh nướng và y chiếc bánh dẻo là 60x + 50y (g).

Theo bài, lượng đường để sản xuất bánh là 500 kg = 500 000 g, nên ta có phương trình bậc nhất hai ẩn x, y biểu thị lượng đường để sản xuất hai loại bánh là:

60x + 50y = 500 000 hay 6x + 5y = 50 000.

Ba nghiệm của phương trình trên là: (5 000; 4 000), (6 000; 2 800), (8 000; 400).

Bài 4

Năm bạn Châu, Hà, Khang, Minh, Phong cùng đi mua sticker để trang trí vở. Có hai loại sticker: loại I giá 2 nghìn đồng/chiếc và loại II giá 3 nghìn đồng/chiếc. Mỗi bạn mua 1 chiếc và tổng số tiền năm bạn phải trả là 12 nghìn đồng. Gọi x và y lần lượt là số sticker loại I và loại II mà năm bạn đã mua.

a) Viết hệ hai phương trình bậc nhất hai ẩn x, y biểu thị mối quan hệ giữa các đại lượng.

b) Cặp số (3; 2) có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?

Lời giải:

a) Do mỗi bạn mua 1 chiếc sticker nên năm bạn đã mua tất cả 5 chiếc sticker, do đó ta có phương trình: x + y = 5. (1)

Số tiền các bạn phải trả khi mua x chiếc sticker loại I là: 2x (nghìn đồng).

Số tiền các bạn phải trả khi mua y chiếc sticker loại II là: 3y (nghìn đồng).

Số tiền các bạn phải trả khi mua các sticker trên là 2x + 3y (nghìn đồng).

Theo bài, tổng số tiền năm bạn phải trả là 12 nghìn đồng nên ta có phương trình: 2x + 3y = 12. (2)

Từ (1) và (2) ta có hệ hai phương trình bậc nhất hai ẩn x, y biểu thị mối quan hệ giữa các đại lượng: \(\left\{ \begin{array}{l}x + y = 5\\2x + 3y = 12;\end{array} \right.\)

b) Thay x = 3 và y = 2 vào mỗi phương trình trong hệ \(\left\{ \begin{array}{l}x + y = 5\\2x + 3y = 12;\end{array} \right.\) ta có:

3 + 2 = 5;

2.3 + 3.2 = 12.

Do đó, cặp số (3; 2) là nghiệm của từng phương trình trong hệ.

Vậy cặp số (3; 2) là nghiệm của hệ phương trình ở câu a.

Bài 5

Để chuẩn bị cho buổi liên hoan của gia đình, bác Ngọc mua hai loại thực phẩm là thịt lợn và cá chép. Giá tiền thịt lợn là 130 nghìn đồng/kg, giá tiền cá chép là 50 nghìn đồng/kg. Bác Ngọc đã chi 295 nghìn để mua 3,5 kg hai loại thực phẩm trên. Gọi x và y lần lượt là số kilôgam thịt lợn và cá chép mà bác Ngọc đã mua.

a) Viết hệ hai phương trình bậc nhất hai ẩn x, y biểu thị mối quan hệ giữa các đại lượng.

b) Cặp số (1,5; 2) có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?

Lời giải:

a) Bác Ngọc đã mua 3,5 kg hai loại thực phẩm (thịt lợn và cá chép) nên ta có phương trình: x + y = 3,5. (1)

Số tiền bác Ngọc đã chi để mua x kilôgam thịt lợn là 130x (nghìn đồng).

Số tiền bác Ngọc đã chi để mua y kilôgam cá chép là 50y (nghìn đồng).

Theo bài, bác Ngọc đã chi 295 nghìn để mua hai loại thực phẩm trên nên ta có phương trình: 130x + 50y = 295. (2)

Từ (1) và (2) ta có hệ phương trình bậc nhất hai ẩn x, y biểu thị mối quan hệ giữa các đại lượng: \(\left\{ \begin{array}{l}x + y = 3,5\\130x + 50y = 295;\end{array} \right.\)

b) Thay x = 1,5 và y = 2 vào mỗi phương trình trong hệ \(\left\{ \begin{array}{l}x + y = 3,5\\130x + 50y = 295;\end{array} \right.\), ta có:

1,5 + 2 = 3,5;

130.1,5 + 50.2 = 195 + 100 = 295.

Do đó, cặp số (1,5; 2) là nghiệm của từng phương trình trong hệ.

Vậy cặp số (1,5; 2) là nghiệm của hệ phương trình ở câu a.

Bài 6

Người ta cần sơn hai loại sản phẩm A, B bằng hai loại sơn: sơn xanh, sơn vàng. Lượng sơn để sơn mỗi loại sản phẩm đó được cho ở Bảng 1 (đơn vị: kg/ 1 sản phẩm).

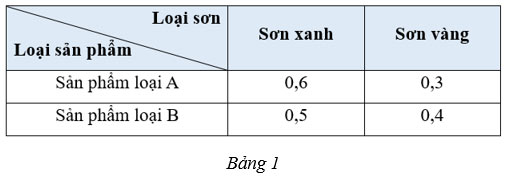
Người ta dự định sử dụng 85 kg sơn xanh và 50 kg sơn vàng để sơn tất cả các sản phẩm của hai loại đó. Gọi x, y lần lượt là số sản phẩm loại A, số sản phẩm loại B được sơn.

a) Viết hệ hai phương trình bậc nhất hai ẩn x, y biểu thị mối quan hệ giữa các đại lượng.

b) Cặp số (100; 50) có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?

Lời giải:

a) Lượng sơn xanh để sơn sản phẩm loại A là: 0,6x (kg).

Lượng sơn xanh để sơn sản phẩm loại B là: 0,5y (kg).

Theo bài, người ta dự định sử dụng 85 kg sơn xanh nên ta có phương trình:

0,6x + 0,5y = 85. (1).

Lượng sơn vàng để sơn sản phẩm loại A là: 0,3x (kg).

Lượng sơn vàng để sơn sản phẩm loại B là: 0,4y (kg).

Theo bài, người ta dự định sử dụng 50 kg sơn vàng nên ta có phương trình:

0,3x + 0,4y = 50. (2).

Từ (1) và (2) ta có hệ hai phương trình bậc nhất hai ẩn x, y biểu thị mối quan hệ giữa các đại lượng: \(\left\{ \begin{array}{l}0,6x + 0,5y = 85\\0,3x + 0,4y = 50;\end{array} \right.\)

b) Thay x = 100 và y = 50 vào mỗi phương trình trong hệ \(\left\{ \begin{array}{l}0,6x + 0,5y = 85\\0,3x + 0,4y = 50;\end{array} \right.\), ta có:

0,6 . 100 + 0,5 . 50 = 60 + 25 = 85;

0,3 . 100 + 0,4 . 50 = 30 + 20 = 50.

Do đó, cặp số (100; 50) là nghiệm của từng phương trình trong hệ.

Vậy cặp số (100; 50) là nghiệm của hệ phương trình ở câu a.