Toán 9 Bài tập cuối chương IV Giải Toán 9 Cánh diều tập 1 trang 92

Giải Toán 9 Bài tập cuối chương IV: Hệ thức lượng trong tam giác vuông là tài liệu vô cùng hữu ích giúp các em học sinh lớp 9 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 9 Cánh diều tập 1 trang 92.

Giải bài tập Toán 9 Cánh diều tập 1 trang 92 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh học tập. Vậy mời thầy cô và các em theo dõi bài viết dưới đây của Eballsviet.com:

Giải Toán 9 Cánh diều Tập 1 trang 92

Bài 1

Cho tam giác ABC vuông tại A có đường cao AH và \(\widehat B = \alpha\)(Hình 40).

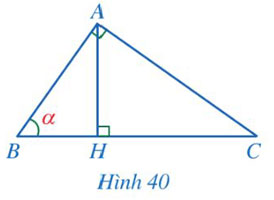
a) Tỉ số \(\frac{{HA}}{{HB}}\) bằng:

A. sinα.

B. cosα.

C. tanα.

D. cotα.

b) Tỉ số \(\frac{{HA}}{{HC}}\) bằng:

A. sinα.

B. cosα.

C. tanα.

D. cotα.

c) Tỉ số \(\frac{{HA}}{{AC}}\) bằng:

A. sinα.

B. cosα.

C. tanα.

D. cotα.

Hướng dẫn giải

a) Chọn đáp án C.

b) Xét tam giác AHC vuông tại H có:

\(\tan C = \frac{{HA}}{{HC}}.\)

Do \(\widehat B + \widehat C = 90^\circ\)nên \(\tan C = \cot B.\)

Vậy \(\cot \alpha = \frac{{HA}}{{HC}}.\)

Chọn đáp án D.

c) Xét tam giác AHC vuông tại H có:

\(\sin C = \frac{{HA}}{{AC}}.\)

Do \(\widehat B + \widehat C = 90^\circ\)nên \(\sin C = \cos B.\)

Vậy \(\cos \alpha = \frac{{HA}}{{AC}}.\)

Chọn đáp án B.

Bài 2

Cho hình thoi ABCD có AB = a,\(\widehat {BAD} = 2\alpha \left( {0^\circ < \alpha < 90^\circ } \right)\). Chứng minh:

a) BD = 2a.sinα;

b) AC = 2a.cosα.

Hướng dẫn giải

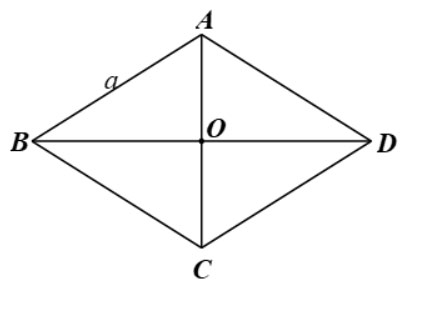
Do \(\widehat {BAD} = 2\alpha \Rightarrow \widehat {OAB} = \alpha .\)

a) Xét tam giác BOA vuông tại O có :

\(BO = AB.\sin \alpha = a.\sin \alpha .\)

Mà \(BD = 2BO = 2a.\sin \alpha .\)

b) Xét tam giác BOA vuông tại O có:

\(CO = AB.\cos \alpha = a.\cos \alpha .\)

Mà \(AC = 2CO = 2a.\cos \alpha .\)

Bài 3

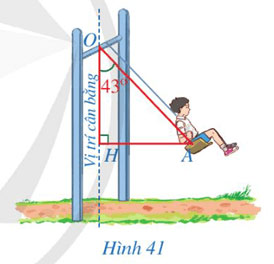
Trong trò chơi xích đu ở Hình 41, khi dây căng xích đu (không dãn) \(OA = 3m\) tạo với phương thẳng đứng một góc là \(\widehat {AOH} = 43^\circ\) thì khoảng cách \(AH\) từ em bé đến vị trí cân bằng là bao nhiêu mét (làm tròn kết quả đến hàng phần trăm)?

Hướng dẫn giải

Xét tam giác \(OHA\) vuông tại \(H\) ta có:

\(AH = OA.\sin \widehat {AOH} = 3.\sin 43^\circ \approx 2,05\left( m \right)\).

Vậy khoảng cách \(AH\) từ em bé đến vị trí cân bằng khoảng 2,05m.

Bài 4

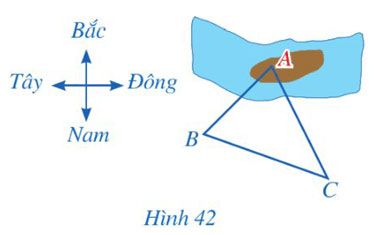
Một người đứng ở vị trí \(B\) trên bờ sông muốn sử dụng la bàn để ước lượng khoảng cách từ vị trí đó đến một vị trí \(A\) ở trên một cù lao giữa dòng sông. Người đó đã làm như sau:

- Sử dụng la bàn, xác định được phương \(BA\) lệch với phương Nam – Bắc về hướng Đông \(52^\circ\).

- Người đó di chuyển đến vị trí \(C\), cách \(B\) một khoảng là 187m. Sử dụng la bàn, xác định được phương \(CA\) lệch với phương Nam – Bắc về hướng Tây \(27^\circ\); \(CB\) lệch với phương Nam – Bắc về hướng Tây \(70^\circ\) (Hình 42).

Em hãy giúp người đó tính khoảng cách \(AB\) từ những dữ liệu trên (làm tròn kết quả đến hàng đơn vị của mét).