Toán 9 Bài 5: Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên Giải Toán 9 Cánh diều tập 1 trang 118, 119, 120, 121, 122, 123

Giải Toán 9 Bài 5: Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên là tài liệu vô cùng hữu ích giúp các em học sinh lớp 9 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 9 Cánh diều tập 1 trang 118, 119, 120, 121, 122, 123.

Giải bài tập Toán 9 Cánh diều tập 1 Bài 5 - Chương V: Đường tròn được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh học tập. Vậy mời thầy cô và các em theo dõi bài viết dưới đây của Eballsviet.com:

Giải Toán 9 Cánh diều Tập 1 trang 122, 123

Bài 1

Quan sát các hình 83, 84, 85, 86.

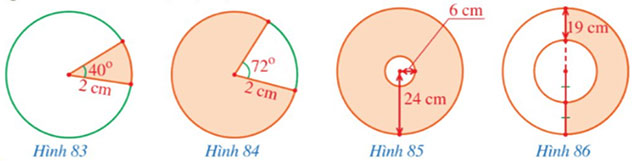
a) Tính diện tích phần được tô màu mỗi hình đó.

b) Tính độ dài cung tròn được tô màu xanh ở mỗi hình 83, 84.

Bài 2

Hình 87 mô tả mặt cắt của chiếc đèn led có dạng hình vành khuyên màu trắng với bán kính các đường tròn lần lượt là 15 cm, 18 cm, 21 cm, 24 cm. Tính diện tích hai hình vành khuyên đó.

Hướng dẫn giải:

Diện tích hình vành khuyên bên trong là: S₁ = π(18² – 15²) = 99π (cm²).

Diện tích hình vành khuyên bên ngoài là S₁ = π(24² – 21²) = 135π (cm²).

Bài 3

Hình 88 mô tả mặt cắt của một khung gỗ có dạng ghép của năm hình: hai nửa hình tròn đường kính 2 cm; hai hình chữ nhật kích thước 2 cm × 8 cm (Hình 88b); một phần tư hình vành khuyên giới hạn bởi hai đường tròn cùng tâm có bán kính lần lượt là 4 cm và 6 cm. Tính diện tích của mặt cắt của khung gỗ đó.

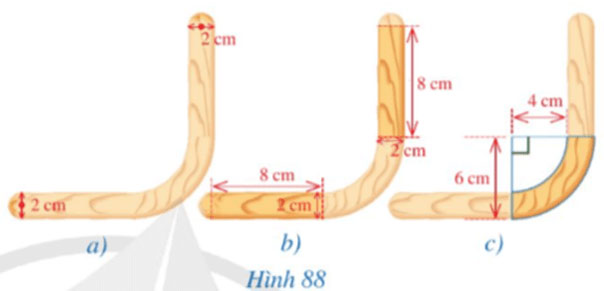
Hướng dẫn giải:

Tổng diện tích hai nửa hình tròn đường kính 2 cm (bán kính 1 cm) chính là diện tích của một hình tròn bán kính 1 cm, và bằng: S₁ = π.1² = π (cm²).

Tổng diện tích hai hình chữ nhật kích thước 2 cm × 8 cm là: S₂ = 2.(2.8) = 32 (cm²).

Diện tích một phần tư hình vành khuyên giới hạn bởi hai đường tròn cùng tâm có bán kính lần lượt là 4 cm và 6 cm là:

S₃=\(\frac{1}{4}\)⋅π(6²−4²)=5π(cm²).

Diện tích của mặt cắt của khung gỗ đó là:

S = S ₁ + S ₂ + S ₃ = π + 32 + 5π = 6π + 32 (cm ² ).

Bài 4

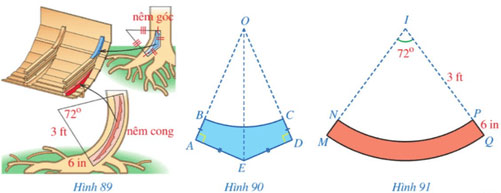
Khi đóng đáy thuyền cho những con thuyền vượt biển, người Vikings sử dụng hai loại nêm: nêm góc và nêm cong (lần lượt tô màu xanh, màu đỏ trong Hình 89). Mặt cắt ABCD của nêm góc có dạng hai tam giác vuông OAE, ODE bằng nhau với cạnh huyền chung và bỏ đi hình quạt tròn OBC (Hình 90), được làm từ những thân cây mọc thẳng. Mặt cắt MNPQ của nêm cong có dạng một phần của hình vành khuyên (Hình 91), được làm từ những thân cây cong. Kích thước của nêm cong được cho như ở Hình 91.

a) Diện tích của nêm cong là bao nhiêu centimét vuông (lấy 1 ft = 30,48 cm, 1 in = 2,54 cm và làm tròn kết quả đến hàng đơn vị)?

b) Cần phải biết những kích thước nào của nêm góc để tính được diện tích của nêm đó?

Hướng dẫn giải:

a)

+ Diện tích quạt tròn \(INP\) là:

\(S = \frac{{\pi {R^2}n}}{{360}} = \frac{{\pi {{.90}^2}.72}}{{360}} = 1620\pi \approx 5087\left( {c{m^2}} \right)\)

+ Diện tích quạt tròn \(IMQ\) là:

\(S = \frac{{\pi {R^2}n}}{{360}} = \frac{{\pi {{\left( {6.2,54.30.3} \right)}^2}.72}}{{360}} = \frac{{\pi .1371,{6^2}.72}}{{360}} \approx 1181448\left( {c{m^2}} \right)\)

+ Diện tích của nêm cong là:

\(S = {S_{IMQ}} - {S_{INP}} \approx 1181448 - 5087 \approx 1176361\left( {c{m^2}} \right)\)

b) Để tính được nêm góc cần biết: diện tích hình \(OAD\), góc \(AOD\), độ dài cạnh \(OB\)