Toán 9 Bài 3: Ứng dụng của tỉ số lượng giác của góc nhọn Giải Toán 9 Cánh diều tập 1 trang 88, 89, 90, 91

Giải Toán 9 Bài 3: Ứng dụng của tỉ số lượng giác của góc nhọn là tài liệu vô cùng hữu ích giúp các em học sinh lớp 9 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 9 Cánh diều tập 1 trang 88, 89, 90, 91.

Giải bài tập Toán 9 Cánh diều tập 1 Bài 3 - Chương IV: Hệ thức lượng trong tam giác vuông được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh học tập. Vậy mời thầy cô và các em theo dõi bài viết dưới đây của Eballsviet.com:

Giải Toán 9 Cánh diều Tập 1 trang 90, 91

Bài 1

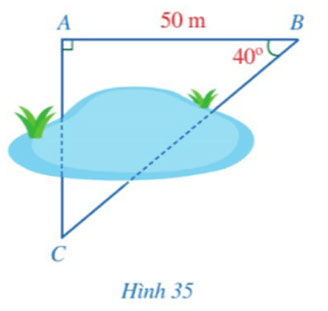
Hình 35 mô tả ba vị trí A, B, C là ba đỉnh của một tam giác vuông và không đo được trực tiếp các khoảng cách từ C đến A và từ C đến B. Biết AB = 50 m, \(\widehat {ABC}\)=40°. Tính các khoảng cách CA và BC (làm tròn kết quả đến hàng đơn vị của mét).

Bài 2

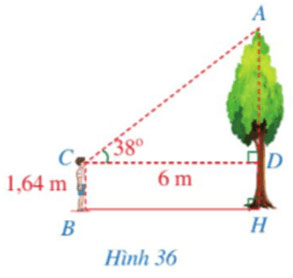
Để ước lượng chiều cao của một cây trong sân trường, bạn Hoàng đứng ở sân trường (theo phương thẳng đứng), mắt bạn Hoàng đặt tại vị trí C cách mặt đất một khoảng CB = DH = 1,64 m và cách cây một khoảng CD = BH = 6 m. Tính chiều cao AH của cây (làm tròn kết quả đến hàng phần trăm của mét), biết góc nhìn ACD bằng 38° minh hoạ ở Hình 36.

Hướng dẫn giải:

Xét ∆ACD vuông tại D, ta có:

AD = CD.tan ACD= 6.tan38^o ≈ 4,69 (m).

Ta có AG = AD + DH ≈ 4,69 + 1,64 = 6,33 (m).

Vậy chiều cao AH của cây khoảng 6,33 m.

Bài 3

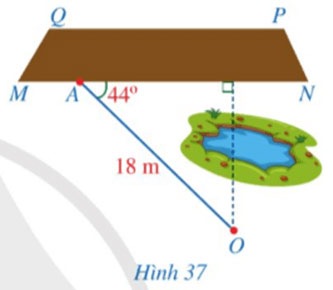
Người ta cần ước lượng khoảng cách từ vị trí O đến khu đất có dạng hình thang MNPQ nhưng không thể đo được trực tiếp, khoảng cách đó được tính bằng khoảng cách từ O đến đường thẳng MN. Người ta chọn vị trí A ở đáy MN và đo được OA = 18 m, \(\widehat {OAN}\)=44° (Hình 37). Tính khoảng cách từ vị trí O đến khu đất (làm tròn kết quả đến hàng phần mười của mét).

Hướng dẫn giải:

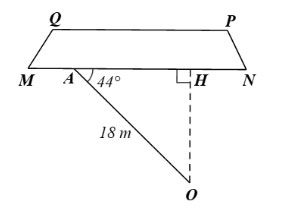
Gọi H là chân đường vuông góc kẻ từ O đến MN.

Xét ∆OAH vuông tại H, ta có: OH = OA.sinA = 18.sin44° ≈ 12,5 (m).

Vậy khoảng cách từ vị trí O đến khu đất khoảng 12,5 m.

Bài 4

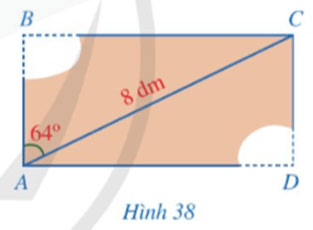
Một mảnh gỗ có dạng hình chữ nhật ABCD với đường chéo AC = 8 dm. Do bảo quản không tốt nên mảnh gỗ bị hỏng phía hai đỉnh B và D. Biết \(\widehat {BAC}\)=64° (Hình 38). Người ta cần biết độ dài AB và AD để khôi phục lại mảnh gỗ ban đầu. Độ dài AB, AD bằng bao nhiêu decimét (làm tròn kết quả đến hàng phần mười)?

Hướng dẫn giải:

Xét ∆ABC vuông tại B, ta có:

AB = AC.cos\(\widehat {BAC}\)= 8.cos64^o ≈ 3,5 (dm).

BC = AC.sin \(\widehat {BAC}\)= 8.sin64^o ≈ 7,2 (dm).

Do ABCD là hình chữ nhật nên AD = BC ≈ 7,2 dm.

Vậy AB ≈ 3,5 dm và AD ≈ 7,2 dm.

Bài 5

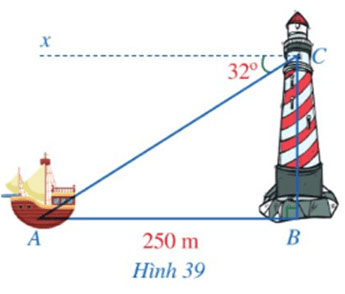
Trên mặt biển, khi khoảng cách AB từ ca nô đến chân tháp hải đăng là 250 m, một người đứng trên tháp hải đăng đó, đặt mắt tại vị trí C và nhìn về phía ca nô theo phương CA tạo với phương nằm ngang Cx một góc là \(\widehat {ACx}\)=32° (Hình 39). Tính chiều cao của tháp hải đăng (làm tròn kết quả đến hàng phần mười của mét), biết AB // Cx và độ cao từ tầm mắt của người đó đến đỉnh tháp hải đăng là 3,2 m.