Giải Toán 9 Bài 2: Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt Giải SGK Toán 9 Hình học Tập 2 (trang 117, 118, 119, 120)
Giải Toán lớp 9 trang 117, 118, 119, 120 tập 2 giúp các bạn học sinh có thêm nhiều gợi ý tham khảo để trả lời các câu hỏi và bài tập của Bài 2 Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt thuộc chương 4 Hình học 9 tập 2.
Giải Toán 9 Bài 2 tập 2 Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa môn Toán. Giải Toán lớp 9 trang 117, 118, 119, 120 tập 2 là tài liệu cực kì hữu ích hỗ trợ các em học sinh trong quá trình giải bài tập. Đồng thời phụ huynh có thể sử dụng để hướng dẫn con em học tập và đổi mới phương pháp giải phù hợp hơn.
Toán 9 Bài 2: Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt
- Lý thuyết Toán 9 Chương 4 Bài 2
- Trả lời câu hỏi Toán 9 Bài 2
- Giải Toán 9 trang 117, 118, 119, 120 tập 2
- Giải Luyện tập Toán 9 trang 119, 120 tập 2
Lý thuyết Toán 9 Chương 4 Bài 2
1. Hình nón
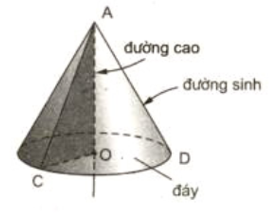
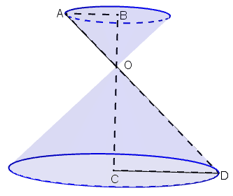
Khi quay tam giác vuông AOC một vòng quanh cạnh OA cố định thì được một hình nón.
+ Điểm A được gọi đỉnh của hình nón.
+ Hình tròn (O) được gọi là đáy của hình nón.
+ Mỗi vị trí của AC được gọi là một đường sinh của hình nón.
+ Đoạn AO được gọi là đường cao của hình nón.
2. Diện tích – thể tích của hình nón
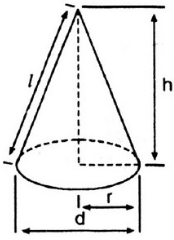
Đặt AC = l; l là đường sinh
Cho hình nón có bán kính đáy R và đường sinh l, chiều cao h.
+ Diện tích xung quanh: Sxq = πRl
+Diện tích toàn phần: Stp = πRl + πR2
3. Hình nón cụt
Khi cắt hình nón bởi một mặt phẳng song song với đáy thì phần hình nón nằm giữa mặt phẳng nói trên và mặt phẳng đáy được gọi là một hình nón cụt.
+ Hai hình tròn (O) và (O') được gọi là hai đáy.
+ Đoạn OO' được gọi là trục. Độ dài OO' là chiều cao.
+ Đoạn AC được gọi là đường sinh.
4. Diện tích – thể tích hình nón cụt
Cho hình nón cụt có các bán kính đáy R và r, chiều cao h, đường sinh l.
+ Diện tích xung qaunh: Sxq = π(R + r)l
+ Thể tích: ![]() \(V=\dfrac {1}{3}\pi h (r_1^2+r_2^2+r_1r_2)\)
\(V=\dfrac {1}{3}\pi h (r_1^2+r_2^2+r_1r_2)\)
Trả lời câu hỏi Toán 9 Bài 2
Chiếc nón (h.88) có dạng mặt xung quanh là một hình nón. Quan sát hình và cho biết, đâu là đường tròn đáy, đâu là mặt xung quanh, đâu là đường sinh của nón.
Gợi ý đáp án
Đường tròn đáy là phần vành rộng nhất của nón
Mặt xung quanh là phần bên ngoài của nón, tính từ đỉnh nón đến đường tròn đáy
Đường sinh là đường thẳng bất kì, nối từ đỉnh đến đường tròn đáy
Giải Toán 9 trang 117, 118, 119, 120 tập 2
Bài 15 (trang 117 SGK Toán 9 Tập 2)
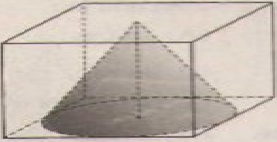
Một hình nón được đặt vào bên trong một hình lập phương như hình vẽ (cạnh của hình lập phương bằng 1) (h.93). Hãy tính:
a) Bán kính đáy của hình nón.
b) Độ dài đường sinh.
Gợi ý đáp án
a) Ta có đường tròn đáy của hình nón nội tiếp trong hình vuông của một mặt của hình lập phương. Do đo bán kính của hình tròn đáy của hình nón bằng một nửa của cạnh hình lập phương và bằng 0,5.
b) Đỉnh của hình nón tiếp xúc với một mặt của hình lập phương nên đường cao của hình nón bằng với cạnh của hình lập phương và bằng 1.
Theo định lí Pitago, độ dài đường sinh của hình nón là:
![]() \(l^2=r^2+h^2 \Rightarrow l= \sqrt{1^2+ 0,5^2}=\dfrac{\sqrt{5}}{2}\)
\(l^2=r^2+h^2 \Rightarrow l= \sqrt{1^2+ 0,5^2}=\dfrac{\sqrt{5}}{2}\)
Bài 16 (trang 117 SGK Toán 9 Tập 2)
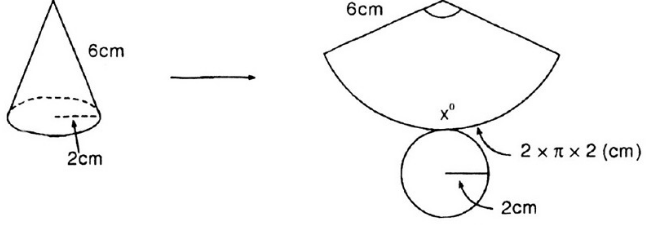
Cắt mặt cắt xung quanh của một hình nón theo một đường sinh và trải phẳng ra thành một hình quạt. Biết bán kính hình quạt tròn bằng độ dài đường sinh và độ dài cung bằng chu vi đáy.
Quan sát hình 94 và tính số đo cung của hình quạt tròn.
Gợi ý đáp án
+ Ta thấy hình nón có bán kính đáy r = 2cm. Suy ra chu vi đáy ![]() \(C = 2\pi r = 2\pi .2 = 4\pi \left( {cm} \right)\)
\(C = 2\pi r = 2\pi .2 = 4\pi \left( {cm} \right)\)
+ Lại thấy hình quạt có bán kính R = 6cm và độ dài cung là ![]() \(l = C = 4\pi \left( {cm} \right)\)
\(l = C = 4\pi \left( {cm} \right)\)
Gọi ![]() \(x^\circ \,\left( {x > 0} \right)\) là số đo cung của hình quạt.
\(x^\circ \,\left( {x > 0} \right)\) là số đo cung của hình quạt.
Khi đó độ dài cung là ![]() \(l = \dfrac{{\pi Rx}}{{180}} \Leftrightarrow \dfrac{{\pi .6.x}}{{180}} = 4\pi \Leftrightarrow 6x = 720 \Leftrightarrow x = 120. (tm)\)
\(l = \dfrac{{\pi Rx}}{{180}} \Leftrightarrow \dfrac{{\pi .6.x}}{{180}} = 4\pi \Leftrightarrow 6x = 720 \Leftrightarrow x = 120. (tm)\)
Vậy số đo cung của hình quạt tròn là ![]() \(120^\circ .\)
\(120^\circ .\)
Bài 17 (trang 117 SGK Toán 9 Tập 2)
Khi quay tam giác vuông để tạo ra một hình nón như hình 87 thì góc CAO gọi là nửa góc ở đỉnh của hình nón. Biết nửa góc ở đỉnh của một hình nón là 30o, độ dài đường sinh là a. Tính số đo cung của hình quạt khi khai triển mặt xung quanh của hình nón.
Gợi ý đáp án
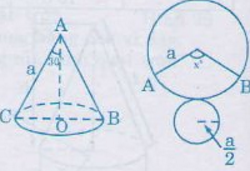
Theo đề bài có ![]() \(\widehat {CAO}=30^0\) nên góc ở đỉnh của hình nón là
\(\widehat {CAO}=30^0\) nên góc ở đỉnh của hình nón là ![]() \(\widehat {CAB}=60^0\), suy ra đường kính của đường tròn đáy của hình nón bằng a (do ∆ABC đều).
\(\widehat {CAB}=60^0\), suy ra đường kính của đường tròn đáy của hình nón bằng a (do ∆ABC đều).
Vậy bán kính đáy của hình nón là ![]() \(\dfrac{a}{2}.\)
\(\dfrac{a}{2}.\)
Chu vi đáy hình nón là ![]() \(C=2\pi\dfrac{a}{2}=\pi a\)
\(C=2\pi\dfrac{a}{2}=\pi a\)
Đường sinh của hình nón là a.
Khai triển mặt xung quanh hình nón ta được hình quạt AOB có bán kính R = a.
Độ dài cung AB có số đo ![]() \(x^0\), bán kính a là
\(x^0\), bán kính a là ![]() \(l=\dfrac{\pi ax}{180}\)
\(l=\dfrac{\pi ax}{180}\)
Nhận thấy độ dài cung AB bằng chu vi đáy hình nón nên ta có phương trình
![]() \(\dfrac{\pi ax}{180}=\pi a\)
\(\dfrac{\pi ax}{180}=\pi a\)
Suy ra :![]() \(x^0=180^0.\)
\(x^0=180^0.\)
Bài 18 (trang 117 SGK Toán 9 Tập 2)
Hình ABCD (h.95) khi quay quanh BC thì tạo ra:
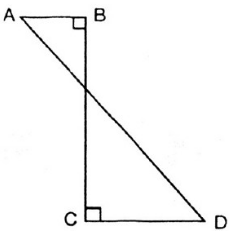
(A) Một hình trụ
(B) Một hình nón
(C) Một hình nón cụt
(D) Hai hình nón
(E) Hai hình trụ
Hãy chọn câu trả lời đúng.
Gợi ý đáp án
Nếu gọi O là giao điểm của BC và AD. Khi quay hình ABCD quanh BC thì có nghĩa là quay tam giác vuông OAB quanh OB và tam giác vuông OCD quanh OC. Mỗi hình quay sẽ tạo ra một hình nón. Vậy hình tạo ra sẽ là hai hình nón.
 Vậy chọn D.
Vậy chọn D.
Bài 19 (trang 118 SGK Toán 9 Tập 2)
Hình khai triển của mặt xung quanh của một hình nón là một hình quạt. Nếu bán kính hình quạt là 16cm, số đo cung là 120 thì độ dài đường sinh của hình nón là:
A. 16 CM
B. 8 cm
C. 16/3 cm
D. 4 cm
E. 16/5 cm
Gợi ý đáp án
Khi khai triển mặt xung quanh của hình nón, ta được một hình quạt có bán kính bằng độ dài đường sinh.
Đề bài cho ta bán kính hình tròn chứa hình quạt là 16cm nên độ dài đường sinh của hình nón là 16cm.
Vậy chọn A.
Bài 20 (trang 118 SGK Toán 9 Tập 2)
Hãy điền đủ vào các ô trống ở bảng sau (xem hình 96):
| Bán kính đáy r(cm) | Đường kính đáy d(cm) | Chiều cao h(cm) | Độ dài đường sinh l(cm) | Thể tích V |
| 10 | 10 | |||
| 10 | 10 | |||
| 10 | 1000 | |||
| 10 | 1000 | |||
| 1000 |
Gợi ý đáp án
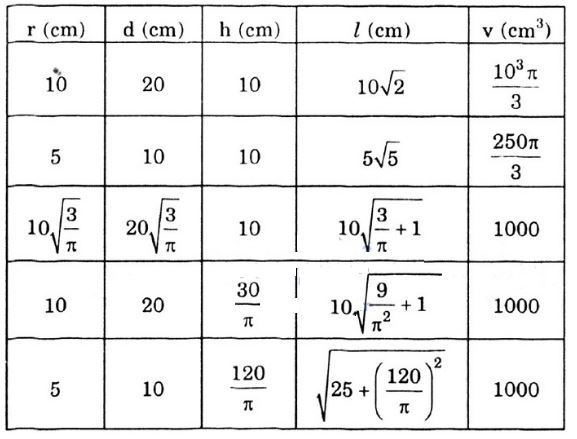
+ Dòng thứ nhất:
d = 2r = 1.10 = 20(cm)
![]() \(l = \sqrt{h^2 + r^2 }= \sqrt{10^2 + 10^2}= 10\sqrt{2}\) (cm)
\(l = \sqrt{h^2 + r^2 }= \sqrt{10^2 + 10^2}= 10\sqrt{2}\) (cm)
![]() \(V = \dfrac{1}{3}\pi r^2h = \dfrac{1}{3}. 10^2. 10. \pi= 10^3. \pi.\dfrac{1}3 (cm^3)\)
\(V = \dfrac{1}{3}\pi r^2h = \dfrac{1}{3}. 10^2. 10. \pi= 10^3. \pi.\dfrac{1}3 (cm^3)\)
+ Dòng thứ hai: ![]() \(r= \dfrac{d}{2}= 5\) (cm)
\(r= \dfrac{d}{2}= 5\) (cm)
![]() \(l = \sqrt{h^2 + r^2}= \sqrt{10^2 + 5^2}= 5\sqrt{5}\) (cm)
\(l = \sqrt{h^2 + r^2}= \sqrt{10^2 + 5^2}= 5\sqrt{5}\) (cm)
![]() \(V = \frac{1}{3}\pi r^2h = \dfrac{1}{3}. 5^2. 10. \pi= 250. \pi.\dfrac{1}3 (cm3)\)
\(V = \frac{1}{3}\pi r^2h = \dfrac{1}{3}. 5^2. 10. \pi= 250. \pi.\dfrac{1}3 (cm3)\)
+ Dòng thứ ba: ![]() \(Khi h = 10cm;V = 1000\,c{m^3}\)
\(Khi h = 10cm;V = 1000\,c{m^3}\)
Ta có ![]() \(V = \dfrac{1}{3}\pi {r^2}h \Leftrightarrow {r^2} = \dfrac{{3V}}{{\pi h}} = \dfrac{{3.1000}}{{\pi .10}} = \dfrac{{300}}{\pi }\, \Rightarrow r = 10\sqrt {\dfrac{3}{\pi }} \,cm\)
\(V = \dfrac{1}{3}\pi {r^2}h \Leftrightarrow {r^2} = \dfrac{{3V}}{{\pi h}} = \dfrac{{3.1000}}{{\pi .10}} = \dfrac{{300}}{\pi }\, \Rightarrow r = 10\sqrt {\dfrac{3}{\pi }} \,cm\)
- Đường kính đáy ![]() \(d = 2r = 20\sqrt {\dfrac{3}{\pi }} \,cm\)
\(d = 2r = 20\sqrt {\dfrac{3}{\pi }} \,cm\)
- Đường sinh ![]() \(l = \sqrt {{h^2} + {r^2}} = \sqrt {100 + \dfrac{{300}}{\pi }} = 10\sqrt {\dfrac{3}{\pi } + 1}\)
\(l = \sqrt {{h^2} + {r^2}} = \sqrt {100 + \dfrac{{300}}{\pi }} = 10\sqrt {\dfrac{3}{\pi } + 1}\)
+ Dòng thứ tư : Khi r = 10cm;![]() \(V = 1000\,c{m^3}\)
\(V = 1000\,c{m^3}\)
Ta có V = ![]() \(\dfrac{1}{3}\pi {r^2}h \Leftrightarrow h = \dfrac{{3V}}{{\pi {r^2}}} = \dfrac{{3.1000}}{{\pi {{.10}^2}}} = \dfrac{{30}}{\pi }cm\)
\(\dfrac{1}{3}\pi {r^2}h \Leftrightarrow h = \dfrac{{3V}}{{\pi {r^2}}} = \dfrac{{3.1000}}{{\pi {{.10}^2}}} = \dfrac{{30}}{\pi }cm\)
- Đường kính đáy d = 2r = 20cm
- Đường sinh ![]() \(l = \sqrt {{h^2} + {r^2}} = \sqrt {\dfrac{{900}}{\pi } + 100} = 10\sqrt {\dfrac{9}{{{\pi ^2}}} + 1}\)
\(l = \sqrt {{h^2} + {r^2}} = \sqrt {\dfrac{{900}}{\pi } + 100} = 10\sqrt {\dfrac{9}{{{\pi ^2}}} + 1}\)
+ Dòng thứ 5: Khi d = 10cm;![]() \(V = 1000c{m^3} ta có r = \dfrac{d}{2} = 5cm\)
\(V = 1000c{m^3} ta có r = \dfrac{d}{2} = 5cm\)
- Lại có ![]() \(V = \dfrac{1}{3}\pi {r^2}h \Leftrightarrow h = \dfrac{{3V}}{{\pi {r^2}}} = \dfrac{{3.1000}}{{\pi {{.5}^2}}} = \dfrac{{120}}{\pi }cm\)
\(V = \dfrac{1}{3}\pi {r^2}h \Leftrightarrow h = \dfrac{{3V}}{{\pi {r^2}}} = \dfrac{{3.1000}}{{\pi {{.5}^2}}} = \dfrac{{120}}{\pi }cm\)
- Đường sinh  \(l = \sqrt {{r^2} + {h^2}} = \sqrt {{5^2} + {{\left( {\dfrac{{120}}{\pi }} \right)}^2}}\)
\(l = \sqrt {{r^2} + {h^2}} = \sqrt {{5^2} + {{\left( {\dfrac{{120}}{\pi }} \right)}^2}}\)
Bài 21 (trang 118 SGK Toán 9 Tập 2)
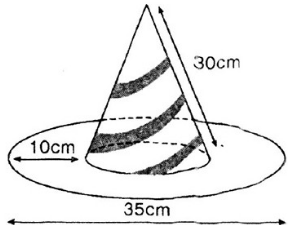
Cái mũ của chú hề với các kích thước cho theo hình vẽ (h.97). Hãy tính tổng diện tích vải cần có để làm nên cái mũ (không kể riềm, mép, phần thừa).
Gợi ý đáp án
Gọi S là diện tích vải cần có, ![]() \({S_{xq}}\) là diện tích xung quanh hình nón,
\({S_{xq}}\) là diện tích xung quanh hình nón, ![]() \({S_{vk}}\) là diện tích hình vành khăn thì
\({S_{vk}}\) là diện tích hình vành khăn thì ![]() \(S = {S_{xq}} + {S_{vk}}\)
\(S = {S_{xq}} + {S_{vk}}\)
+ Đường kính đường tròn lớn là 35cm nên bán kính đường tròn lớn là ![]() \(R = \dfrac{{35}}{2} = 17,5cm\)
\(R = \dfrac{{35}}{2} = 17,5cm\)
Suy ra bán kính đường tròn nhỏ là r = 17,5 - 10 = 7,5cm.
Với ![]() \(\pi = 3,14\) ta có
\(\pi = 3,14\) ta có
+ Diện tích hình vành khăn là ![]() \({S_{vk}} = \pi {R^2} - \pi {r^2} = \pi .17,{5^2} - \pi .7,{5^2} = 785c{m^2}\,\)
\({S_{vk}} = \pi {R^2} - \pi {r^2} = \pi .17,{5^2} - \pi .7,{5^2} = 785c{m^2}\,\)
+ Hình nón có đường sinh l = 30cm và bán kính đáy r = 7,5cm nên có diện tích xung quanh là ![]() \({S_{xq}} = \pi rl = \pi .7,5.30 = 706,5c{m^2}\)
\({S_{xq}} = \pi rl = \pi .7,5.30 = 706,5c{m^2}\)
Vậy diện tích vải cần làm mũ là ![]() \(S = {S_{vk}} + {S_{xq}} = 785 + 706,5 = 1491,5c{m^2} .\)
\(S = {S_{vk}} + {S_{xq}} = 785 + 706,5 = 1491,5c{m^2} .\)
Bài 22 (trang 118 SGK Toán 9 Tập 2)
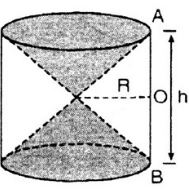
Hình 98 cho ta hình ảnh của một cái đồng hồ cát với các kích thước kèm theo (AO = OB).
Hãy so sánh tổng thể tích của hai hình nón và thể tích của hình trụ.
Gợi ý đáp án
Nhận thấy hai hình nón trên hình bằng nhau.
Chiều cao của 1 hình nón là:![]() \(\dfrac{h}{2}\)
\(\dfrac{h}{2}\)
Thể tích của hai hình nón là:
![]() \(2{V_{nón}}=2.\dfrac{1}{3} \pi .R^2 .\dfrac{h}{2}= \dfrac{\pi R^2 h}{3}\)
\(2{V_{nón}}=2.\dfrac{1}{3} \pi .R^2 .\dfrac{h}{2}= \dfrac{\pi R^2 h}{3}\)
Thể tích của hình trụ là: ![]() \({V_{trụ}} = \pi {R^2}h\)
\({V_{trụ}} = \pi {R^2}h\)
Nên  \(\dfrac{2V_{nón}}{V_{trụ}}= \dfrac{\dfrac{\pi R^2 h}{3}}{\pi R^2 h}= \dfrac{1}{3}.\)
\(\dfrac{2V_{nón}}{V_{trụ}}= \dfrac{\dfrac{\pi R^2 h}{3}}{\pi R^2 h}= \dfrac{1}{3}.\)
Giải Luyện tập Toán 9 trang 119, 120 tập 2
Bài 23 (trang 119 SGK Toán 9 Tập 2)
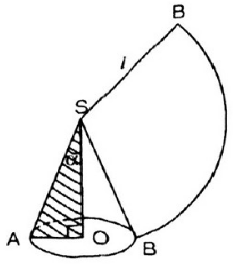
Viết công thức tính nửa góc ở đỉnh của một hình nón (góc α của tam giác vuông OAS – hình 99) sao cho diện tích mặt khai triển của mặt nón bằng một một phần tư diện tích của hình tròn (bán kính SA).
Gợi ý đáp án
Diện tích hình quạt :
![]() \(S_{quạt} = \dfrac{\pi r^2 n^o}{360^o}= \dfrac{\pi.l^2.90}{360}=\dfrac{\pi.l^2}4.\)
\(S_{quạt} = \dfrac{\pi r^2 n^o}{360^o}= \dfrac{\pi.l^2.90}{360}=\dfrac{\pi.l^2}4.\)
Diện tích xung quanh của hình nón: ![]() \({S_{xq}} = \pi rl\)
\({S_{xq}} = \pi rl\)
Theo đầu bài ta có: ![]() \({S_{xq}} = S_{quạt} \Rightarrow πrl= \dfrac{\pi.l^2}4.\)
\({S_{xq}} = S_{quạt} \Rightarrow πrl= \dfrac{\pi.l^2}4.\)
Vậy l = 4r.
Suy ra ![]() \(\sin \alpha =\dfrac {OA}{SA}= \dfrac{r}l = \dfrac {1}4\) (vì l=4r.)
\(\sin \alpha =\dfrac {OA}{SA}= \dfrac{r}l = \dfrac {1}4\) (vì l=4r.)
Vậy ![]() \(\alpha= {14^0}28'.\)
\(\alpha= {14^0}28'.\)
Bài 24 (trang 119 SGK Toán 9 Tập 2)
Hình khai triển của mặt xung quanh của một hình nón là một hình quạt, bán kính hình quạt đó là 16cm, số đo cung là 120o. Tang của nửa góc ở đỉnh của hình nón là:
![]() \((A) \dfrac{\sqrt{2}}4\)
\((A) \dfrac{\sqrt{2}}4\)
![]() \((B) \dfrac{\sqrt{2}}2\)
\((B) \dfrac{\sqrt{2}}2\)
![]() \((C) \sqrt{2}\)
\((C) \sqrt{2}\)
![]() \((D) 2\sqrt{2}\)
\((D) 2\sqrt{2}\)
Gợi ý đáp án
Đường sinh của hình nón là l = 16.
Độ dài cung AB của đường tròn chứa hình quạt là ![]() \(\dfrac {\pi .16.120}{180}=\dfrac{32. \pi}{3},\) và độ dài cung này bằng chu vi đáy hình nón C= 2πr suy ra
\(\dfrac {\pi .16.120}{180}=\dfrac{32. \pi}{3},\) và độ dài cung này bằng chu vi đáy hình nón C= 2πr suy ra ![]() \(2 \pi r=\dfrac{32. \pi}{3}\Rightarrow r= \dfrac{16}{3}.\)
\(2 \pi r=\dfrac{32. \pi}{3}\Rightarrow r= \dfrac{16}{3}.\)
Trong tam giác vuông AOS có:
 \(h= \sqrt{16^2-{\left( {\dfrac{{16}}{3}} \right)^2}}= 16\sqrt{\dfrac{8}{9}}= \dfrac{32\sqrt{2}}{3}\)
\(h= \sqrt{16^2-{\left( {\dfrac{{16}}{3}} \right)^2}}= 16\sqrt{\dfrac{8}{9}}= \dfrac{32\sqrt{2}}{3}\)
Vậy ta có: ![]() \(\tan \alpha= \dfrac{r}{h} = \dfrac{\sqrt{2}}{4}.\)
\(\tan \alpha= \dfrac{r}{h} = \dfrac{\sqrt{2}}{4}.\)
Chọn A.
Bài 25 (trang 119 SGK Toán 9 Tập 2)
Hãy tính diện tích xung quanh của hình nón cụt biết hai bán kính đáy là a, b (a < b) và độ dài đường sinh là l (a, b, l có cùng đơn vị đo).
Gợi ý đáp án
Kí hiệu như hình vẽ. SA=l1;AB=l;OB=b;O'A=a.
Vì O'A//OB ![]() \(\Rightarrow \Delta SO'A \backsim \Delta SOB\)
\(\Rightarrow \Delta SO'A \backsim \Delta SOB\)
![]() \(\Rightarrow \dfrac{{SA}}{{SB}} = \dfrac{{OA}}{{OB}} \Leftrightarrow \dfrac{{{l_1}}}{{l + {l_1}}} = \dfrac{a}{b} \Leftrightarrow b{l_1} = al + a{l_1} \Leftrightarrow {l_1}\left( {b - a} \right) = al \Leftrightarrow {l_1} = \dfrac{a}{{b - a}}l\)
\(\Rightarrow \dfrac{{SA}}{{SB}} = \dfrac{{OA}}{{OB}} \Leftrightarrow \dfrac{{{l_1}}}{{l + {l_1}}} = \dfrac{a}{b} \Leftrightarrow b{l_1} = al + a{l_1} \Leftrightarrow {l_1}\left( {b - a} \right) = al \Leftrightarrow {l_1} = \dfrac{a}{{b - a}}l\)
Suy ra ![]() \(SB = l + {l_1} = l + \dfrac{a}{{b - a}}l = \dfrac{b}{{b - a}}l\)
\(SB = l + {l_1} = l + \dfrac{a}{{b - a}}l = \dfrac{b}{{b - a}}l\)
Diện tích xung quanh hình nón lớn là ![]() \({S_1} = \pi .b.SB = \pi .b.\dfrac{b}{{b - a}}l = \dfrac{{{b^2}}}{{b - a}}\pi l\)
\({S_1} = \pi .b.SB = \pi .b.\dfrac{b}{{b - a}}l = \dfrac{{{b^2}}}{{b - a}}\pi l\)
Diện tích xung quanh hình nón nhỏ là ![]() \({S_2} = \pi .a.SA = \pi .a.\dfrac{a}{{b - a}}l = \dfrac{{{a^2}}}{{b - a}}\pi l\)
\({S_2} = \pi .a.SA = \pi .a.\dfrac{a}{{b - a}}l = \dfrac{{{a^2}}}{{b - a}}\pi l\)
Diện tích xung quanh hình nón cụt là ![]() \(S = {S_1} - {S_2} = \dfrac{{{b^2}}}{{b - a}}\pi l - \dfrac{{{a^2}}}{{b - a}}\pi l = \pi l.\dfrac{{{b^2} - {a^2}}}{{b - a}} = \left( {a + b} \right)\pi l\)
\(S = {S_1} - {S_2} = \dfrac{{{b^2}}}{{b - a}}\pi l - \dfrac{{{a^2}}}{{b - a}}\pi l = \pi l.\dfrac{{{b^2} - {a^2}}}{{b - a}} = \left( {a + b} \right)\pi l\)
Vậy diện tích xung quanh nón cụt là ![]() \(S = \pi \left( {a + b} \right)l\)
\(S = \pi \left( {a + b} \right)l\)
Bài 26 (trang 119 SGK Toán 9 Tập 2)
Hãy điền đủ vào các ô trống cho ở bảng sau (đơn vị độ dài: cm):
| Bán kính đáy r(cm) | Đường kính đáy d(cm) | Chiều cao h(cm) | Độ dài đường sinh l(cm) | Thể tích V(cm3) |
| 5 | 12 | |||
| 16 | 15 | |||
| 7 | 25 | |||
| 40 | 29 |
Gợi ý đáp án
Lấy ![]() \(\pi=3,14\)
\(\pi=3,14\)
+ Dòng thứ nhất: Khi r = 5cm;h = 12cm ta có
- Đường kính d = 2r = 2.5 = 10cm
- Đường sinh ![]() \(l = \sqrt {{r^2} + {h^2}} = \sqrt {{5^2} + {{12}^2}} = 13\,cm\)
\(l = \sqrt {{r^2} + {h^2}} = \sqrt {{5^2} + {{12}^2}} = 13\,cm\)
- Thể tích ![]() \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {.5^2}.12 = 100\pi=314 \left( {c{m^3}} \right)\)
\(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {.5^2}.12 = 100\pi=314 \left( {c{m^3}} \right)\)
+ Dòng thứ hai: Khi d = 16cm;h = 15cm ta có
- Bán kính ![]() \(r = \dfrac{d}{2} = \dfrac{{16}}{2} = 8cm\)
\(r = \dfrac{d}{2} = \dfrac{{16}}{2} = 8cm\)
- Đường sinh ![]() \(l = \sqrt {{r^2} + {h^2}} = \sqrt {{8^2} + {{15}^2}} = 17\,cm\)
\(l = \sqrt {{r^2} + {h^2}} = \sqrt {{8^2} + {{15}^2}} = 17\,cm\)
- Thể tích ![]() \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {.8^2}.15 = 320\pi =1004,8\left( {c{m^3}} \right)\)
\(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {.8^2}.15 = 320\pi =1004,8\left( {c{m^3}} \right)\)
+ Dòng thứ ba: Khi r = 7cm;l = 25cm ta có
- Đường kính d = 2r = 2.7 = 14cm
- Vì ![]() \({l^2} = {h^2} + {r^2} \Rightarrow h = \sqrt {{l^2} - {r^2}} = \sqrt {{{25}^2} - {7^2}} = 24cm\)
\({l^2} = {h^2} + {r^2} \Rightarrow h = \sqrt {{l^2} - {r^2}} = \sqrt {{{25}^2} - {7^2}} = 24cm\)
- Thể tích ![]() \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {.7^2}.24 = 392\pi \approx 1230,9\left( {c{m^3}} \right)\)
\(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {.7^2}.24 = 392\pi \approx 1230,9\left( {c{m^3}} \right)\)
+ Dòng thứ tư: Khi d = 40cm;l = 29cm ta có
- Đường kính ![]() \(r = \dfrac{d}{2} = \dfrac{{40}}{2} = 20cm\)
\(r = \dfrac{d}{2} = \dfrac{{40}}{2} = 20cm\)
- Vì ![]() \({l^2} = {h^2} + {r^2} \Rightarrow h = \sqrt {{l^2} - {r^2}} = \sqrt {{{29}^2} - {{20}^2}} = 21cm\)
\({l^2} = {h^2} + {r^2} \Rightarrow h = \sqrt {{l^2} - {r^2}} = \sqrt {{{29}^2} - {{20}^2}} = 21cm\)
Thể tích ![]() \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {.20^2}.21 = 2800\pi =8792 \left( {c{m^3}} \right)\)
\(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {.20^2}.21 = 2800\pi =8792 \left( {c{m^3}} \right)\)
Từ đó ta được bảng sau
| Bán kính đáy r(cm) | Đường kính đáy d(cm) | Chiều cao h(cm) | Độ dài đường sinh l(cm) | Thể tích V(cm3) |
| 5 | 10 | 12 | 13 | 314 |
| 8 | 16 | 15 | 17 | 320 π |
| 7 | 14 | 24 | 25 | 392 π |
| 20 | 40 | 21 | 29 | 2800 π |
Bài 27 (trang 119 SGK Toán 9 Tập 2)
Một dụng cụ gồm một phần có dạng hình trụ, phần còn lại có dạng hình nón. Các kích thước cho trên hình 100. Hãy tính:
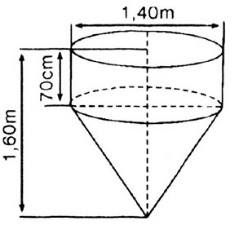
a) Thể tích của dụng cụ này.
b) Diện tích mặt ngoài của dụng cụ (không tính nắp đậy).
Gợi ý đáp án
Lấy ![]() \(\pi=3,14\)
\(\pi=3,14\)
a) Thể tích cần tính gồm một hình trụ, đường kính đáy 1,4m, chiều cao 70cm=0,7m, và một hình nón, bán kính đáy bằng bán kính hình trụ, chiều cao hình nón bằng 0,9m.
Thể tích hình trụ:
 \(V_{trụ} \displaystyle =\pi {R^2}h = 3,14.{\left( {{{1,4} \over 2}} \right)^2}.0,7=1,077({m^3}).\)
\(V_{trụ} \displaystyle =\pi {R^2}h = 3,14.{\left( {{{1,4} \over 2}} \right)^2}.0,7=1,077({m^3}).\)
Thể tích hình nón:
 \(\displaystyle V_{nón}={1 \over 3}.3,14.{\left( {{{1,4} \over 2}} \right)^2}.0,9 = 0,462({m^3}).\)
\(\displaystyle V_{nón}={1 \over 3}.3,14.{\left( {{{1,4} \over 2}} \right)^2}.0,9 = 0,462({m^3}).\)
Vậy thể tích cái phễu:
![]() \(V =V_{trụ}+ V_{nón} =1,077+0,462=1,539({m^3}).\)
\(V =V_{trụ}+ V_{nón} =1,077+0,462=1,539({m^3}).\)
b) Diện tích cần tính gồm diện tích xung quanh hình trụ và diện tích xung quanh hình nón. Đường sinh của hình nón là:
![]() \(l = \sqrt{h^2 + r^2}=\sqrt{0,9^2+(1,4/2)^2}= \sqrt{1,3} \approx 1,14(m)\)
\(l = \sqrt{h^2 + r^2}=\sqrt{0,9^2+(1,4/2)^2}= \sqrt{1,3} \approx 1,14(m)\)
![]() \(\displaystyle S_{xq \, \, trụ}= 2\pi rh = 2.3,14.{{1,4} \over 2}.0,7 = 3,077({m^2})\)
\(\displaystyle S_{xq \, \, trụ}= 2\pi rh = 2.3,14.{{1,4} \over 2}.0,7 = 3,077({m^2})\)
![]() \(S_{xq \, \, nón}=\displaystyle \pi rl = 3,14.{{1,4} \over 2}.1,4 = 2,506({m^2})\)
\(S_{xq \, \, nón}=\displaystyle \pi rl = 3,14.{{1,4} \over 2}.1,4 = 2,506({m^2})\)
Vậy diện tích toàn phần của phễu:
![]() \(S=S_{xq \, \, trụ}+S_{xq \, \, nón} = 3,077 + 2,506 = 5,583 (m^2)\)
\(S=S_{xq \, \, trụ}+S_{xq \, \, nón} = 3,077 + 2,506 = 5,583 (m^2)\)
Bài 28 (trang 120 SGK Toán 9 Tập 2)
Một cái xô bằng inox có dạng hình nón cụt đựng hóa chất, có các kích thước cho ở hình 101 (đơn vị: cm).
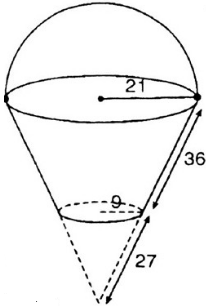
a) Hãy tính diện tích xung quanh của xô.
b) Khi xô chứa đầy hóa chất thì dung tích của nó là bao nhiêu?
Gợi ý đáp án
Gọi l là đường sinh của hình nón lớn.
Theo định lý Ta-lét ta có:![]() \(\dfrac{l}{l-36}=\dfrac{21}{9}\)
\(\dfrac{l}{l-36}=\dfrac{21}{9}\)
Suy ra 9.l=21.(l-36) ![]() \(\Rightarrow 12l=432\Rightarrow l=63\)
\(\Rightarrow 12l=432\Rightarrow l=63\)
a) Diện tích cần tính gồm diện tích xung quanh của hình xung quanh của hình nón cụt và diện tích hình tròn đáy có bán kính 9cm.
Đường sinh của hình nón lớn là l = 63 cm.
Đường sinh của hình nón nhỏ là 63-36=27 cm.
Diện tích xung quanh của hình nón lớn, hình nón nhỏ:
![]() \(S_{xq \, \, hình \, \, nón \, \, lớn} =πrl= 3,14.21.63 =4154,22 \, cm^2.\)
\(S_{xq \, \, hình \, \, nón \, \, lớn} =πrl= 3,14.21.63 =4154,22 \, cm^2.\)
![]() \(S_{xq \, \, hình \, \, nón \, \, nhỏ} =3,14.9.27 =763,02 \, cm^2.\)
\(S_{xq \, \, hình \, \, nón \, \, nhỏ} =3,14.9.27 =763,02 \, cm^2.\)
Diện tích xung quanh của xô chính là diện tích xung quanh hình nón cụt:
![]() \(S_{xq \, \, hình \, \, nón \, \, cụt} = S_{xq \, \, hình \, \, nón \, \, lớn} - S_{xq \, \, hình \, \, nón \, \, nhỏ} \\\)
\(S_{xq \, \, hình \, \, nón \, \, cụt} = S_{xq \, \, hình \, \, nón \, \, lớn} - S_{xq \, \, hình \, \, nón \, \, nhỏ} \\\)
= 4154,22 - 763,02 = 3391,2 .
b) Chiều cao của hình nón lớn:
![]() \(h= \sqrt{63^2 + 21^2} = 59,397 \, cm.\)
\(h= \sqrt{63^2 + 21^2} = 59,397 \, cm.\)
Chiều cao của hình nón nhỏ:
![]() \(h'= \sqrt{27^2 - 9^2}= 25,546 \, cm.\)
\(h'= \sqrt{27^2 - 9^2}= 25,546 \, cm.\)
Thể tích của hình nón lớn:
![]() \(V_{hình \, \, nón \, \, lớn}={1 \over 3}\pi rh = {1 \over 3}.3,{14.21^2}.59,397 = 27416,467(c{m^3}).\)
\(V_{hình \, \, nón \, \, lớn}={1 \over 3}\pi rh = {1 \over 3}.3,{14.21^2}.59,397 = 27416,467(c{m^3}).\)
Thể tích hình nón nhỏ:
![]() \(\displaystyle V_{hình \, \, nón \, \, nhỏ}={1 \over 3}\pi rh = {1 \over 3}.3,{14.9^2}.25,456\)
\(\displaystyle V_{hình \, \, nón \, \, nhỏ}={1 \over 3}\pi rh = {1 \over 3}.3,{14.9^2}.25,456\)
![]() \(= 2158,160(c{m^3})\)
\(= 2158,160(c{m^3})\)
Khi xô chứa đầy hóa chất thì dung tích của nó là:
![]() \(\displaystyle V=V_{hình \, \, nón \, \, lớn}-V_{hình \, \, nón \, \, nhỏ}\)
\(\displaystyle V=V_{hình \, \, nón \, \, lớn}-V_{hình \, \, nón \, \, nhỏ}\)
![]() \(=27416,467 - 2158,160 \approx 25258 \, cm^3.\)
\(=27416,467 - 2158,160 \approx 25258 \, cm^3.\)
Bài 29 (trang 120 SGK Toán 9 Tập 2)
Cối xay gió của Đôn-ki-hô-tê (từ tác phẩm của Xéc-van-téc (Cervantès).
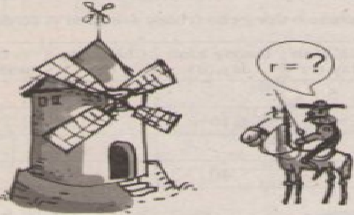
Phần trên của cối xay gió có dạng một hình nón (h.102). Chiều cao của hình nón là 42cm và thể tích của nó là 17 600 cm3.
Em hãy giúp chàng Đôn-ki-hô-tê tính bán kính đáy của hình nón (làm tròn kết quả đên chữ số thập phân thứ hai).
Gợi ý đáp án
Theo đề bài ta có:
![]() \(V = 17 600 \, cm^3, h = 42 \, cm.\)
\(V = 17 600 \, cm^3, h = 42 \, cm.\)
Từ công thức ![]() \(V = \dfrac{1}{3}\pi r^2 h\) ta suy ra
\(V = \dfrac{1}{3}\pi r^2 h\) ta suy ra ![]() \(r =\sqrt{\dfrac{3V}{\pi h}}.\)
\(r =\sqrt{\dfrac{3V}{\pi h}}.\)
Thay số vào ta được:
 \(r =\sqrt{\dfrac{3. 17600}{3,14.42 }}\)
\(r =\sqrt{\dfrac{3. 17600}{3,14.42 }}\)
\Rightarrow r ≈ 20 cm.
Vậy bán kính của hình tròn là r = 20 cm.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:












 Đề thi giữa kì 2 lớp 9
Đề thi giữa kì 2 lớp 9
 Đề thi học kì 2 Lớp 9
Đề thi học kì 2 Lớp 9
 Đề thi giữa kì 1 lớp 9
Đề thi giữa kì 1 lớp 9
 Đề thi học kì 1 Lớp 9
Đề thi học kì 1 Lớp 9
 Toán 9
Toán 9
 Toán 9 Kết nối tri thức
Toán 9 Kết nối tri thức
 Toán 9 Cánh Diều
Toán 9 Cánh Diều
 Toán 9 Chân trời sáng tạo
Toán 9 Chân trời sáng tạo
 Văn 9 Kết nối tri thức
Văn 9 Kết nối tri thức









