Toán 11 Bài tập cuối chương VIII Giải Toán 11 Cánh diều trang 116, 117 - Tập 2

Giải Toán 11 Bài tập cuối chương VIII là tài liệu vô cùng hữu ích giúp các em học sinh lớp 11 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 11 Cánh diều tập 2 trang 116, 117.

Toán 11 Cánh diều tập 2 trang 116, 117 được biên soạn đầy đủ, chi tiết trả lời các câu hỏi từ bài 1 đến bài 8 chương Quan hệ vuông góc trong không gian - Phép chiếu song song giúp các bạn có thêm nhiều nguồn ôn tập đối chiếu với kết quả mình đã làm. Vậy sau đây là nội dung chi tiết giải Toán 11 trang 116, 117 Cánh diều Tập 2, mời các bạn cùng theo dõi tại đây.

Giải Toán 11 trang 116, 117 Cánh diều - Tập 2

Bài 1

Cho hình lập phương MNPQ.M'N'P'Q' có cạnh bằng a

a) Góc giữa đường thẳng MN và M'P' bằng:

A. 30^∘

B. 45^∘

C. 60^∘

D. 90^∘

b) Gọi là số đo góc giữa đường thẳng M'P và mặt phẳng (MNPQ). Giá trị bằng:

A. 1

B. 2

C. \(\sqrt{2}\)

D. \(\frac{1}{\sqrt{2} }\)

c) Số đo của góc nhị diện [N, MM', P] bằng:

A. 30^∘

B. 45^∘

C. 60^∘

D. 90^∘

d) Khoảng cách từ điểm M đến mặt phẳng (NQQ'N') bằng:

A. a

B. \(\frac{a}{\sqrt{2} }\)

C. a\(\sqrt{2}\)

D. \(\frac{a}{2}\)

Gợi ý đáp án

a) Đáp án B

b) Đáp án D

c) Đáp án B

d) Đáp án B

Bài 2

Cho hình hộp chữ nhật MNPQ.M'N'P'Q' có MN=2a,MQ=3a,MM′=4a. Khoảng cách giữa hai đường thẳng NP và M'N' bằng

A. 2a

B. 3a

C. 4a

D. 5a

Gợi ý đáp án

Đáp án C

Bài 3

Cho khối lăng trụ có diện tích đáy bằng a² và chiều cao bằng 3a. Thể tích của khối lăng trụ đó bằng:

A. a³

B. 3a³

C. a\(\frac{a^{3} }{3}\)

D. 9a³

Gợi ý đáp án

Đáp án B

Bài 4

Cho khối chóp có diện tích đáy là a2 và chiều cao là 3a. Thể tích của khối chóp bằng:

A. a³

B. 3a³

C. a\(\frac{a^{3} }{3}\)

D. 9a³

Gợi ý đáp án

Đáp án A

Bài 5

Cho tứ diện OABC thỏa mãn OA = a, OB = b, OC = c,

\(\widehat{AOB}\) = \(\widehat{BOC}\) = \(\widehat{COA}\) = 90^∘. Thể tích của khối tứ diện OABC bằng:

A. abc

B. \(\frac{abc}{2}\)

C. \(\frac{abc}{3}\)

D. \(\frac{abc}{6}\)

Gợi ý đáp án

Đáp án D

Bài 6

Cho hình chóp S.ABC có: SA ⊥ (ABC), AC ⊥ BC, SA = BC = a\(\sqrt{3}\), AC = a

a) Tính góc giữa hai đường thẳng SA và BC

b) Tính góc giữa đường thẳng SC và mặt phẳng (ABC)

c) Tính số đo góc nhị diện [B, SA, C]

d) Tính khoảng cách từ B đến mặt phẳng (SAC)

e) Tính khoảng cách giữa hai đường thẳng SA và BC

g) Tính thể tích của khối chóp S.ABC

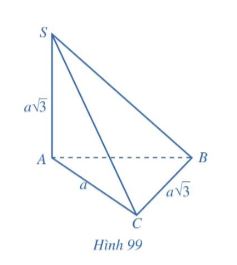
Gợi ý đáp án

a) SA ⊥ (ABC) => SA ⊥ BC => (SA, BC) = \(90^{\circ}\)

b) SA ⊥ (ABC) => (SC, (ABC)) = (SC, AC) = \(\widehat{SCA}\)

Có tam giác SAC vuông tại A

=> \(tan\widehat{SCA}=\frac{SA}{AC}=\frac{a\sqrt{3}}{a}=\sqrt{3}\)

=> \(\widehat{SCA}=60^{\circ}\)

c) \(SA \perp (ABC) => SA\perp AB, SA\perp AC\)

=> \(\widehat{BAC}\) là góc nhị diện [B,SA,C]

=> \(tan \widehat{BAC}=\frac{BC}{AC}=\frac{a\sqrt{3}}{a}=\sqrt{3}\)

=> \(\widehat{BAC}=60^{\circ}\)

d) Có \(SA \perp BC, AC \perp BC => BC \perp (SAC)\)

=> d (B,(SAC)) = BC = \(a\sqrt{3}\)

e) \(SA \perp (ABC) => SA \perp AC, AC\perp BC\)

=> d (SA,BC) = AC = a

g) \(S_{\Delta ABC}=\frac{1}{2}AC\cdot BC=\frac{a^{2}\sqrt{3}}{2}\)

h = SA = \(a\sqrt{3}\)

=> \(V_{S.ABC}=\frac{1}{3}\cdot S_{\Delta ABC}.SA=\frac{a^{3}}{2}\)

Bài 7

Cho hình lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh bằng a. Gọi M là trung điểm của AB (Hình 100).

a) Tính góc giữa hai đường thẳng AB và B'C'.

b) Tính góc giữa đường thẳng A’B và mặt phẳng (ABC).

c) Tính số đo của góc nhị diện [B, CC,M).

d) Chứng minh rằng CC’ // (ABB’A’). Tính khoảng cách giữa đường thẳng CC và mặt phẳng (ABB’A’).

e) Chứng minh rằng CM ⊥ (ABB'A’). Tính khoảng cách giữa hai đường thẳng CC” và A’M.

g) Tính thể tích của khối lăng trụ tam giác đều ABC.A’B’C’ và thể tích khối chóp A’.MBC.

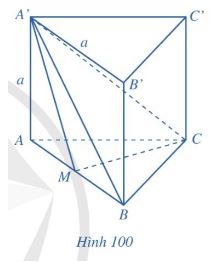
Gợi ý đáp án

a) BCC'B' là hình chữ nhật => BC // B'C'

=> (AB, B'C') = (AB,BC) = \(\widehat{ABC}=60^{\circ}\)

b) Có tam giác AA'B vuông tại A => \(tan\widehat{AB'A}=\frac{AA'}{AB}=\frac{a}{a}=1 => \widehat{ABA'}=45^{\circ}\)

c) Có CC' ⊥ (ABC) => CC' ⊥ BC, CC' ⊥ CM

=> \(\widehat{BCM}\) là góc nhị diện [B, CC', M]

Có tam giác ABC đều => \(\widehat{BCM}=\frac{1}{2}\widehat{ACB}=30^{\circ}\)

d) Có SA ⊥ (ABC) => SA ⊥ CM

mà tam giác ABC đều => CM ⊥ AB

=> CM ⊥ (ABB'A')

=> CMCM = \(\frac{AB\sqrt{3}}{2}=\frac{a\sqrt{3}}{2}\)

- Có CC' // (ABB'A')

=> d (CC', (ABB'A'))= d(C, (ABB'A')) = CM = \(\frac{a\sqrt{3}}{2}\)

e) Có CM ⊥ (ABB'A') => CM ⊥ A'M

=> CC' ⊥ (ABC) => CC' ⊥ CM

=> d (CC', A'M) = CM = \(\frac{a\sqrt{3}}{2}\)

g) \(S_{\Delta ABC}=\frac{AB^{2}\sqrt{3}}{4}=\frac{a^{2}\sqrt{3}}{4} , h=AA'=a\)

=> \(V_{ABC.A'B'C'}=S_{\Delta ABC}.AA'=\frac{a^{2}\sqrt{3}}{4}.a=\frac{a^{3}\sqrt{3}}{4}\)

Có \(S_{\Delta MBC}=\frac{1}{2}S_{\Delta ABC}=\frac{a^{2}\sqrt{3}}{8}\)

=> \(V_{A'.MBC}=\frac{1}{3}S_{\Delta MBC}.AA'=\frac{1}{3}\cdot \frac{a^{2}\sqrt{3}}{8}\cdot a=\frac{a^{3}\sqrt{3}}{24}\)

Bài 8

Đền Kukulcan (Hình 101) là một kim tự tháp Trung Mỹ nằm ở khu di tích Chichen Itza, Mexico, được người Maya xây vào khoảng từ thế kỉ IX đến thế kỉ XII. Phần thân của đền, không bao gồm ngôi đền nằm phía trên, có dạng một khối chóp cụt tứ giác đều (không tính cầu thang và coi các mặt bên là phẳng) với độ dài đáy dưới là 55,3 m, chiều cao là 24 m, góc giữa cạnh bên và mặt phẳng đáy là khoảng 47.