Toán 11 Bài 5: Khoảng cách Giải Toán 11 Cánh diều trang 100, 101, 102,103, 104, 105, 106 - Tập 2
Toán lớp 11 trang 106 Cánh diều tập 2 là tài liệu vô cùng hữu ích mà Eballsviet.com muốn giới thiệu đến quý thầy cô cùng các bạn học sinh lớp 11 tham khảo.
Giải Toán 11 Cánh diều Bài 5 Khoảng cách được biên soạn đầy đủ, chi tiết trả lời các câu hỏi phần bài tập trang 100, 101, 102,103, 104, 105, 106. Qua đó giúp các bạn học sinh có thể so sánh với kết quả mình đã làm. Vậy sau đây là nội dung chi tiết giải Toán 11 trang 106 Cánh diều Tập 2, mời các bạn cùng theo dõi tại đây.
Giải Toán 11 trang 106 Cánh diều - Tập 2
Bài 1
Hình 76 gợi nên hình ảnh hai mặt phẳng (P) và (Q) song song với nhau. Cột gỗ cao 4,2 m. Khoảng cách giữa (P) và (Q) là bao nhiêu mét?
Gợi ý đáp án
Khoảng cách giữa (P) và (Q) là cây cột gỗ gao 4,2m
Bài 2
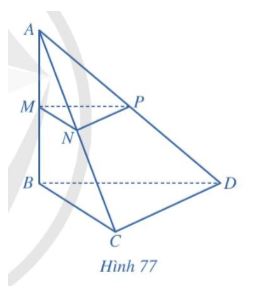
Cho hình tứ diện ABCD có AB = a, BC = b, ![]() \(\widehat{ABC}\) =
\(\widehat{ABC}\) = ![]() \(\widehat{ABD}\) =
\(\widehat{ABD}\) = ![]() \(\widehat{BCD}\) = 90∘. Gọi M, N, P lần lượt là trung điểm của AB, AC, AD
\(\widehat{BCD}\) = 90∘. Gọi M, N, P lần lượt là trung điểm của AB, AC, AD
a) Tính khoảng cách từ điểm C đến đường thẳng AB.
b) Tính khoảng cách từ điểm D đến mặt phẳng (ABC).
c) Tính khoảng cách giữa hai đường thẳng AB và CD.
Gợi ý đáp án
a) Có ![]() \(\widehat{ABC}\) = 90∘
\(\widehat{ABC}\) = 90∘
=> AB ⊥ BC => d(C,AB) = BC = b
b) Có ![]() \(AB\perp BC, AB\perp BD\)
\(AB\perp BC, AB\perp BD\)
=> AB ⊥ (BCD)
=> AB ⊥ CD
mà BC ⊥ CD (Vì ![]() \(\widehat{BCD}\) = 90∘)
\(\widehat{BCD}\) = 90∘)
=> CD ⊥ (ABC)
=> d(D,(ABC)) = CD = ![]() \(\sqrt{BD^{2} - BC^{2} } = \sqrt{c^{2}-b^{2} }\)
\(\sqrt{BD^{2} - BC^{2} } = \sqrt{c^{2}-b^{2} }\)
c) AB ⊥ BC, BC ⊥ CD => d(AB,CD) = BC = b
Bài 3
Với giả thiết ở Bài tập 2, hãy:
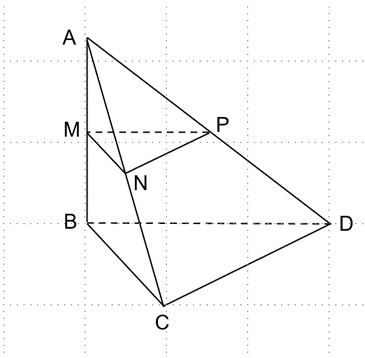
a) Chứng minh rằng MN // BC. Tính khoảng cách giữa hai đường thẳng MN và BC.
b) Chứng minh rằng MP // (BCD). Tính khoảng cách từ đường thẳng MP đến mặt phẳng (BCD).
c) Chứng minh rằng (MNP) || (BCD). Tính khoảng cách giữa hai mặt phẳng (MNP) và (BCD).
Gợi ý đáp án
a) Có M là trung điểm của AB, N là trung điểm của AC
=> MN là đường trung bình của tam giác ABC
=> MN // BC
- Có AB ⊥ BC => MB ⊥ BC => d(MN,BC) = MB = ![]() \(\frac{1}{2}\)AB =
\(\frac{1}{2}\)AB = ![]() \(\frac{a}{2}\)
\(\frac{a}{2}\)
b) Có M là trung điểm của AB, P là trung điểm của AD
=> MP là đường trung bình của tam giác ABD
=> MP // BD
mà BD ⊂ (BCD)
=> MP // (BCD)
Có AB ⊥ (BCD) => MB ⊥ (BCD)
=> d(MP,(BCD)) = d(M,(BCD)) = MB = ![]() \(\frac{a}{2}\)
\(\frac{a}{2}\)
c) Có MN // BC, BC ⊂ (BCD)
=> MN // (BCD)
mà MP // (BCD)
=> (MNP) // (BCD)
=> d((MNP), (BCD)) = d(M,(BCD)) = MB = ![]() \(\frac{a}{2}\)
\(\frac{a}{2}\)
Bài 4
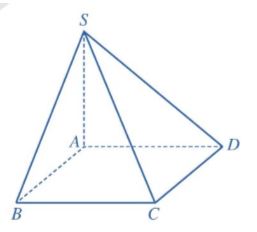
Cho hình chóp S.ABCD có SA ⊥ (ABCD), đáy ABCD là hình vuông cạnh a, SA = a (Hình 78).
a) Tính khoảng cách từ điểm S đến đường thẳng CD.
b) Tính khoảng cách từ điểm D đến mặt phẳng (SAB).
c) Tính khoảng cách từ điểm A đến mặt phẳng (SCD).
Gợi ý đáp án
a) Có ![]() \(SA\perp (ABCD) => SA\perp CD\)
\(SA\perp (ABCD) => SA\perp CD\)
Có ABCD là hình vuông => ![]() \(AD \perp CD\)
\(AD \perp CD\)
=> ![]() \(CD \perp (SAD) => CD\perp SD\)
\(CD \perp (SAD) => CD\perp SD\)
=> ![]() \(d(S,CD)=SD=\sqrt{SA^{2}+AD^{2}}=a\sqrt{2}\)
\(d(S,CD)=SD=\sqrt{SA^{2}+AD^{2}}=a\sqrt{2}\)
b) ![]() \(SA\perp (ABCD)=>SA\perp AD\)
\(SA\perp (ABCD)=>SA\perp AD\)
ABCD là hình vuông => ![]() \(AB\perp AD\)
\(AB\perp AD\)
=> ![]() \(AD\perp (SAB)=>d(D,(SAB))=AD=a\)
\(AD\perp (SAB)=>d(D,(SAB))=AD=a\)
c) Kẻ ![]() \(AH\perp SD\)
\(AH\perp SD\)
![]() \(CD\perp (SAD) => CD\perp AH\)
\(CD\perp (SAD) => CD\perp AH\)
=> ![]() \(AH\perp (SCD)=>d(A,(SCD))=AH\)
\(AH\perp (SCD)=>d(A,(SCD))=AH\)
Tam giác SAD vuông tại A có đường cao AH
=> ![]() \(AH=\frac{SA.AD}{SD}=\frac{a\sqrt{2}}{2}\)
\(AH=\frac{SA.AD}{SD}=\frac{a\sqrt{2}}{2}\)
Bài 5
Với giả thiết ở Bài tập 4, hãy:
a) Chứng minh rằng BC // (SAD) và tính khoảng cách giữa BC và mặt phẳng (SAD).
b) Chứng minh rằng BD ⊥ (SAC) và tính khoảng cách giữa hai đường thẳng BD và SC.
Gợi ý đáp án
a) ABCD là hình vuông => BC // AD
mà ![]() \(AD \subset (SAD)\)
\(AD \subset (SAD)\)
=> ![]() \(BC // (SAD) => d(BC,(SAD))=d(B, (SAD))\)
\(BC // (SAD) => d(BC,(SAD))=d(B, (SAD))\)
![]() \(SA\perp (ABCD) => SA\perp AB\)
\(SA\perp (ABCD) => SA\perp AB\)
ABCD là hình vuông
=> ![]() \(AB\perp AD => AB\perp (SAD) => d(B, (SAD))=AB=a\)
\(AB\perp AD => AB\perp (SAD) => d(B, (SAD))=AB=a\)
b) ABCD là hình vuông => ![]() \(BD \perp AC\)
\(BD \perp AC\)
![]() \(SA\perp (ABCD) => SA\perp BD\)
\(SA\perp (ABCD) => SA\perp BD\)
=> ![]() \(BD \perp (SAC)\)
\(BD \perp (SAC)\)
Gọi ![]() \(O=AC\cap BD\), kẻ
\(O=AC\cap BD\), kẻ ![]() \(OH\perp SC\)
\(OH\perp SC\)
Có ![]() \(BD \perp (SAC) => BD \perp OH\)
\(BD \perp (SAC) => BD \perp OH\)
=> d(BD, SC) = OH
Có tam giác ABC vuông tại B
=> ![]() \(AC=a\sqrt{2}\)
\(AC=a\sqrt{2}\)
=> ![]() \(OC=\frac{1}{2}AC=\frac{a\sqrt{2}}{2}\)
\(OC=\frac{1}{2}AC=\frac{a\sqrt{2}}{2}\)
Có ![]() \(SA\perp (ABCD) => SA\perp AC\)
\(SA\perp (ABCD) => SA\perp AC\)
=> Tam giác SAC vuông tại A
=> ![]() \(SC=a\sqrt{3}\)
\(SC=a\sqrt{3}\)
Có ![]() \(\Delta SAC\sim \Delta OHC (g.g)\)
\(\Delta SAC\sim \Delta OHC (g.g)\)
=> ![]() \(\frac{SA}{OH}=\frac{SC}{OC}\)
\(\frac{SA}{OH}=\frac{SC}{OC}\)
=> ![]() \(OH=\frac{SA.OC}{SC}=\frac{a\sqrt{6}}{6}\)
\(OH=\frac{SA.OC}{SC}=\frac{a\sqrt{6}}{6}\)
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:












 Đề thi học kì 1 Lớp 11
Đề thi học kì 1 Lớp 11
 Đề thi học kì 2 Lớp 11
Đề thi học kì 2 Lớp 11
 Soạn văn 11 Kết nối tri thức
Soạn văn 11 Kết nối tri thức
 Soạn văn 11 Chân trời sáng tạo
Soạn văn 11 Chân trời sáng tạo
 Soạn văn 11 Cánh Diều
Soạn văn 11 Cánh Diều
 Toán 11 Kết nối tri thức
Toán 11 Kết nối tri thức
 Toán 11 Chân trời sáng tạo
Toán 11 Chân trời sáng tạo
 Toán 11 Cánh Diều
Toán 11 Cánh Diều
 Hóa 11 KNTT
Hóa 11 KNTT