Toán 11 Bài 2: Các phép biến đổi lượng giác Giải Toán 11 Cánh diều trang 16, 17, 18, 19, 20, 21

Bài trước

Mục lục

Bài sau

Toán lớp 11 tập 1 trang 16, 17, 18, 19, 20, 21 Cánh diều là tài liệu vô cùng hữu ích mà Eballsviet.com muốn giới thiệu đến quý thầy cô cùng các bạn học sinh lớp 11 tham khảo.

Giải Toán 11 Cánh diều Bài 2 Các phép biến đổi lượng giác được biên soạn đầy đủ, chi tiết trả lời các câu hỏi phần bài tập cuối bài trang 20, 21. Qua đó giúp các bạn học sinh có thể so sánh với kết quả mình đã làm. Vậy sau đây là nội dung chi tiết Toán 11 tập 1 Bài 2 Các phép biến đổi lượng giác Cánh diều trang 20, 21, mời các bạn cùng theo dõi tại đây.

Toán 11 Bài 2: Các phép biến đổi lượng giác

Giải Toán 11 Tập 1 trang 15 Cánh diều

Giải Toán 11 Tập 1 trang 15 Cánh diều

Bài 1 trang 20

Cho cosa = $\frac{3}{5}$ $\frac{3}{5}$ với 0< a < $\frac{\pi }{2}$ $\frac{\pi }{2}$.

Tính: sin(a + $\frac{\pi }{6}$ $\frac{\pi }{6}$), cos(a − $\frac{\pi }{3}$ $\frac{\pi }{3}$), tan(a+ $\frac{\pi }{4}$ $\frac{\pi }{4}$).

Gợi ý đáp án

Vì 0 < a < $\frac{\pi }{2}$ $\frac{\pi }{2}$ nên sina > 0

Áp dụng công thức sina² + cos²a = 1, suy ra sina = $\frac{4}{5}$ $\frac{4}{5}$, tana = $\frac{4}{3}$ $\frac{4}{3}$.

Ta có: sin(a+ $\frac{\pi }{6}$ $\frac{\pi }{6}$) = sinacos $\frac{\pi }{6}$ $\frac{\pi }{6}$+ cosasin $\frac{\pi }{6}$ $\frac{\pi }{6}$ = $\frac{3+4\sqrt{3} }{10}$ $\frac{3+4\sqrt{3} }{10}$

cos(a− $\frac{\pi }{3}$ $\frac{\pi }{3}$) = cosacos $\frac{\pi }{3}$ $\frac{\pi }{3}$+ sinasin $\frac{\pi }{3}$ $\frac{\pi }{3}$ = $\frac{3+4\sqrt{3} }{10}$ $\frac{3+4\sqrt{3} }{10}$

tan(a + $\frac{\pi }{4}$ $\frac{\pi }{4}$) = $\frac{tana+tan\frac{\pi }{4} }{1-tanatan\frac{\pi }{4}}$ $\frac{tana+tan\frac{\pi }{4} }{1-tanatan\frac{\pi }{4}}$ = −7.

Bài 2 trang 20

Tính:

A = sin(a − 17^∘)cos(a + 13^∘) − sin(a + 13^∘)cos(a − 17^∘);

B = cos(b + $\frac{\pi }{3}$ $\frac{\pi }{3}$)cos( $\frac{\pi }{6}$ $\frac{\pi }{6}$− b) − sin(b + $\frac{\pi }{3}$ $\frac{\pi }{3}$)sin( $\frac{\pi }{6}$ $\frac{\pi }{6}$ − b).

Gợi ý đáp án

A = sin(a − 17^∘)cos(a + 13^∘) − sin(a + 13^∘)cos(a − 17^∘)

= sin(a − 17^∘− a − 13^∘) = sin(−30^∘) = −12

B = cos(b + $\frac{\pi }{3}$ $\frac{\pi }{3}$)cos( $\frac{\pi }{6}$ $\frac{\pi }{6}$− b) − sin(b + $\frac{\pi }{3}$ $\frac{\pi }{3}$)sin( $\frac{\pi }{6}$ $\frac{\pi }{6}$ − b)

= cos(b + $\frac{\pi }{3}$ $\frac{\pi }{3}$ + $\frac{\pi }{6}$ $\frac{\pi }{6}$ − b) = cos $\frac{\pi }{2}$ $\frac{\pi }{2}$ = 0

Bài 3 trang 20

Cho tan(a + b) = 3, tan(a − b) = 2. Tính: tan2a, tan2b.

Gợi ý đáp án

Ta có: tan(a + b) = 3 ⇔ $\frac{tana+tanb}{1-tanatanb}=3$ $\frac{tana+tanb}{1-tanatanb}=3$ (1)

tan(a − b) = 2 ⇔ $\frac{tana-tanb}{1+tanatanb}=2$ $\frac{tana-tanb}{1+tanatanb}=2$ (2)

tan2a = $\frac{2tana}{1-tan^{2}a}$ $\frac{2tana}{1-tan^{2}a}$ , tan2b = $\frac{2tanb}{1-tan^{2}b}$ $\frac{2tanb}{1-tan^{2}b}$

Cộng hai vế của phương trình (1) và (2), suy ra: 2tana = 5−tanatanb ⇔ tana = $\frac{5-tanatanb}{2}$ $\frac{5-tanatanb}{2}$. Do đó: tan2a = $\frac{4(5-tanatanb)}{(7-tanatanb)(tanatanb-3)}$ $\frac{4(5-tanatanb)}{(7-tanatanb)(tanatanb-3)}$

Trừ hai vế của phương trình (1) và (2), suy ra: 2tanb = 1 − 5tanatanb ⇔ tanb = $\frac{1-5tanatanb}{2}$ $\frac{1-5tanatanb}{2}$ Do đó: $\frac{4(1-5tanatanb)}{(3-5tanatanb)(5tanatanb+1)}$ $\frac{4(1-5tanatanb)}{(3-5tanatanb)(5tanatanb+1)}$

Bài 4 trang 20

Cho sina = $\frac{2}{\sqrt{5} }$ $\frac{2}{\sqrt{5} }$. Tính: cos2a,cos4a.

Gợi ý đáp án

cos2a =1 − 2sin²a = $-\frac{3}{5}$ $-\frac{3}{5}$

cos4a = cos(2.2a) = 1 − 2sin²2a = 1 − 2(1−cos²2a) = $-\frac{7}{25}$ $-\frac{7}{25}$

Bài 5 trang 20

Cho sina + cosa = 1. Tính: sin2a.

Gợi ý đáp án

(sina+cosa)² = 1⇔ 1 + 2sinacosa = 1 ⇔ sin2a = 0

Bài 6 trang 21

Cho cos2a = $\frac{1}{3}$ $\frac{1}{3}$ với $\frac{\pi }{2}$ $\frac{\pi }{2}$ < a < π. Tính: sina,cosa,tana.

Gợi ý đáp án

Vì $\frac{\pi }{2}$ $\frac{\pi }{2}$ < a < π, suy ra: sina > 0, cosa < 0, tana < 0

cos2a = 1 − 2sin²a = $\frac{1}{3}$ $\frac{1}{3}$ ⇔ sin²a = $\frac{1}{3}$ $\frac{1}{3}$ ⇔ sina = $\frac{\sqrt{3} }{3}$ $\frac{\sqrt{3} }{3}$

cos2a = 2cos²a − 1 = $\frac{1}{3}$ $\frac{1}{3}$ ⇔ cos²a = $\frac{2}{3}$ $\frac{2}{3}$ ⇔ cosa = $-\frac{\sqrt{6} }{3}$ $-\frac{\sqrt{6} }{3}$

tana = $\frac{sina}{cosa} =\frac{\sqrt{2} }{2}$ $\frac{sina}{cosa} =\frac{\sqrt{2} }{2}$

Bài 7 trang 21 :

Cho cos2x = $\frac{1}{4}$ $\frac{1}{4}$

Tính: A = cos(x + $\frac{\pi }{6}$ $\frac{\pi }{6}$)cos(x − $\frac{\pi }{6}$ $\frac{\pi }{6}$); B = sin(x + $\frac{\pi }{3}$ $\frac{\pi }{3}$)sin(x − $\frac{\pi }{3}$ $\frac{\pi }{3}$).

Gợi ý đáp án

Áp dụng công thức: cosacosb = $\frac{1}{2}$ $\frac{1}{2}$[cos(a + b) + cos(a − b)]

⇒ A = cos(x + $\frac{\pi }{6}$ $\frac{\pi }{6}$)cos(x − $\frac{\pi }{6}$ $\frac{\pi }{6}$) = $\frac{1}{2}$ $\frac{1}{2}$[cos2x + cos $\frac{\pi }{3}$ $\frac{\pi }{3}$] = $\frac{3}{8}$ $\frac{3}{8}$

Áp dụng công thức: sinasinb = $-\frac{1}{2}$ $-\frac{1}{2}$[cos(a + b) − cos(a − b)]

⇒ B = sin(x + $\frac{\pi }{3}$ $\frac{\pi }{3}$)sin(x − $\frac{\pi }{3}$ $\frac{\pi }{3}$) = $-\frac{1}{2}$ $-\frac{1}{2}$[cos2x − cos $\frac{2\pi }{3}$ $\frac{2\pi }{3}$] = $-\frac{3}{8}$ $-\frac{3}{8}$.

Bài 8 trang 21

Rút gọn biểu thức: $A=\frac{sinx+sin2x+sin3x}{cosx+cos2x+cos3x}$ $A=\frac{sinx+sin2x+sin3x}{cosx+cos2x+cos3x}$.

Gợi ý đáp án

Ta có: sinx + sin2x + sin3x = (sinx + sin3x) + sin2x = 2sin2xcosx + sin2x

= sin2x(2cosx + 1)

Tương tự: cosx + cos2x + cos3x = (cosx + cos3x) + cos2x = 2cos2xcosx + cos2x

= cos2x(2cosx + 1)

Suy ra: $A=\frac{sinx+sin2x+sin3x}{cosx+cos2x+cos3x}=\frac{sin2x}{cos2x}=tan2x$ $A=\frac{sinx+sin2x+sin3x}{cosx+cos2x+cos3x}=\frac{sin2x}{cos2x}=tan2x$

Bài 9 trang 21

Một sợi cáp R được gắn vào một cột thẳng đứng ở vị trí cách mặt đất 14 m. Một sợi cáp S khác cũng được gắn vào cột đó ở vị trí cách mặt đất 12 m. Biết rằng hai sợi cáp trên cùng được gắn với mặt đất tại một vị trí cách chân cột 15 m (Hình 17).

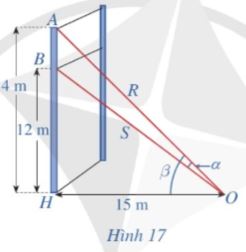
a) Tính tanα, ở đó α là góc giữa hai sợi cáp trên.

b) Tìm góc α (làm tròn kết quả đến hàng đơn vị theo đơn vị độ).

Gợi ý đáp án

a) Gọi β là góc tạo thành của sợi cáp R với mặt đất; γ là góc tạo thành của sợi cáp S với mặt đất.

Do đó: α = β − γ.

Ta có: tanα = tan(β − γ) = $\frac{tan\beta -tan\gamma }{1+tan\beta tan\gamma }=\frac{\frac{14}{15}-\frac{12}{15} }{1+\frac{14}{15}.\frac{12}{15} }=\frac{10}{131}$ $\frac{tan\beta -tan\gamma }{1+tan\beta tan\gamma }=\frac{\frac{14}{15}-\frac{12}{15} }{1+\frac{14}{15}.\frac{12}{15} }=\frac{10}{131}$

b) tanα = $\frac{10}{131}$ $\frac{10}{131}$ ⇒ α ≈ 0,076.

Bài 10 trang 21

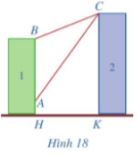
Có hai chung cư cao tầng xây cạnh nhau với khoảng cách giữa chúng là HK = 20 m. Để đảm bảo an ninh, trên nóc chung cư thứ hai người ta lắp camera ở vị trí C. Gọi A, B lần lượt là vị trí thấp nhất, cao nhất trên chung cư thứ nhất mà camera có thể quan sát được (Hình 18). Hãy tính số đo góc ACB (phạm vi camera có thể quan sát được ở chung cư thứ nhất). Biết rằng chiều cao của chung cư thứ hai là CK = 32 m, AH = 6 m, BH = 24 m (làm tròn kết quả đến hàng phần mười theo đơn vị độ).

Gợi ý đáp án

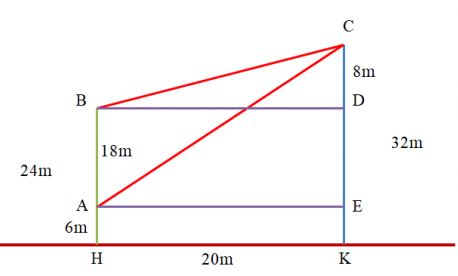
Gọi D, E nằm trên đường thẳng CK sao cho BD, AE ∥ HK.

Từ hình vẽ, ta có: $\hat{ACB}=\hat{BCD} -\hat{ACE}$ $\hat{ACB}=\hat{BCD} -\hat{ACE}$

Ta có: tan $\hat{ACB}$ $\hat{ACB}$ = tan( $\hat{BCD}-\hat{ACE}$ $\hat{BCD}-\hat{ACE}$)

Áp dụng công thức tan(a − b) = $\frac{tana-tanb}{1+tanatanb}$ $\frac{tana-tanb}{1+tanatanb}$

Suy ra: tan( $\hat{BCD}-\hat{ACE}$ $\hat{BCD}-\hat{ACE}$) = $\frac{45}{76}$ $\frac{45}{76}$ nên tan $\hat{ACB}$ $\hat{ACB}$ = $\frac{45}{76}$ $\frac{45}{76}$.

Do đó: $\hat{ACB}$ $\hat{ACB}$ = 30.63^∘.

Chia sẻ bởi: