Tài liệu ôn thi cấp tốc lý thuyết Vật lý 12 luyện thi THPT Quốc gia 2025 Lý thuyết Lý 12 (Chương trình mới)

Tài liệu ôn thi cấp tốc lý thuyết Vật lý 12 luyện thi THPT Quốc gia 2025 theo chương trình mới, giúp các em học sinh hệ thống toàn bộ kiến thức lý thuyết trọng tâm nhất của môn Vật lí, để ôn thi hiệu quả.

Lý thuyết ôn thi Vật lí THPT Quốc gia 2025 gồm 30 trang, tóm tắt toàn bộ kiến thức lý thuyết của 4 chương: Vật lí nhiệt, Khí lí tưởng, Từ trường và Vật lí hạt nhân. Ngoài ra, các em có thể tham khảo thêm Công thức Vật lí 12. Vậy mời các em cùng theo dõi bài viết dưới đây của Eballsviet.com:

Tổng hợp lý thuyết Lý 12 ôn thi THPT Quốc gia 2025

CHƯƠNG 1. VẬT LÍ NHIỆT
CHỦ ĐỀ 1. CẤU TRÚC VÀ SỰ CHUYỂN THỂ

I. Mô hình động học phân tử

Mô hình động học phân tử gồm những nội dung cơ bản:

• ­ Các chất được cấu tạo từ các hạt riêng biệt là phân tử gọi chung cho phân tử, nguyên tử, ion.
• ­ Các phân tử chuyển động không ngừng, nhiệt độ càng cao tốc độ càng lớn (chuyển động nhiệt)
• ­ Giữa các phân tử có lực hút và lực đẩy, gọi chung là lực liên kết phân tử

II. Cấu trúc của vật chất

III. SỰ CHUYỂN THỂ

1. Sự chuyển thể

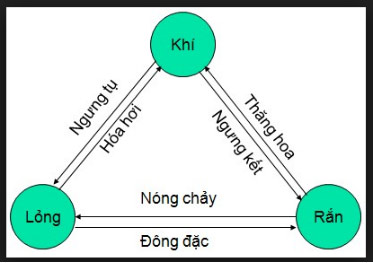
2. Dùng mô hình động học phân tử giải thích sự chuyển thể

­ Trong khi chuyển động hỗn loạn, các phân tử va chạm vào nhau, truyền năng lượng cho nhau => chuyển động hỗn loạn càng nhanh, khoảng cách càng tăng, lực liên kết càng yếu.

a) Sự hóa hơi

• ­ Sự hóa hơi có thể xảy ra dưới hai hình thức là bay hơi và sôi.
• ­ Sự bay hơi là sự hóa hơi xảy ra ở mặt thoáng của chất lỏng.
• ­ Sự sôi là sự hóa hơi xảy ra đồng thời ở bên trong và trên mặt thoáng chất lỏng.

b) Sự nóng chảy

• Sự nóng chảy là quá trình chuyển từ thể rắn sang thể lỏng
• Chất rắn kết tinh có nhiệt độ nóng chảy xác định (ở một áp suất cụ thể), chất rắn vô định hình không có nhiệt động nóng chảy xác định.

CHỦ ĐỀ 2. NỘI NĂNG. ĐỊNH LUẬT I NHIỆT ĐỘNG LỰC HỌC

1. Khái niệm nội năng

•  Tổng động năng và thế năng của các phân tử cấu tạo nên vật được gọi là nội năng của vật. Nội năng được kí hiệu bằng chữ U và có đơn vị là jun (J).
• Nội năng của một vật phụ thuộc vào nhiệt độ và thể tích của vật.

2. Các cách làm thay đổi nội năng

• Thực hiện công: Quá trình thực hiện công làm cho nội năng của vật thay đổi, vật nhận công thì nội năng tăng, hệ thực hiện công cho vật khác thì nội năng giảm.
• Truyền nhiệt: Khi hai vật có nhiệt độ khác nhau tiếp xúc với nhau thì xảy ra quá trình truyền nhiệt. Quá trình này làm thay đổi nội năng của các vật.
• Trong quá trình truyền nhiệt không có sự chuyển hoá năng lượng từ dạng này sang dạng khác mà chỉ có sự truyền nội năng từ vật này sang vật khác.

...

>> Tải file để tham khảo toàn bộ tài liệu!