Toán 6 Bài 2: Hai đường thẳng cắt nhau. Hai đường thẳng song song Giải Toán lớp 6 trang 83 - Tập 2 sách Cánh diều

Bài trước

Mục lục

Bài sau

Giải Toán lớp 6 trang 83 tập 2 Cánh diều giúp các bạn học sinh có thêm nhiều gợi ý tham khảo để trả lời các câu hỏi phần Khởi động, Hoạt động, Luyện tập vận dụng và bài tập trong SGK bài 2 Hai đường thẳng cắt nhau - Hai đường thẳng song song thuộc chương 6 Hình học phẳng.

Toán 6 Cánh diều tập 2 trang 83 Tập 2 được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa môn Toán lớp 6. Giải Toán lớp 6 trang 83 Cánh diều là tài liệu cực kì hữu ích hỗ trợ các em học sinh trong quá trình giải bài tập. Đồng thời phụ huynh có thể sử dụng để hướng dẫn con em học tập và đổi mới phương pháp giải phù hợp hơn.

Giải Toán 6 trang 83 Cánh diều - Tập 2

Câu hỏi Khởi động Toán 6 Bài 2

Quan sát một phần bản đồ giao thông ở TP. Hồ Chí Minh và đọc tên một số đường phố.

Hai đường phố nào gợi Gợi ý đáp án nên hình ảnh hai đường thẳng song song? Hai đường thẳng cắt nhau?

Lời giải:

Một số đường phố xuất hiện ở bản đồ trên là:

Nguyễn Đình Chiểu, Nguyễn Thị Minh Khai, Pasteur, Tam Kỳ khởi nghĩa, Lê Duẩn, Phạm Ngọc Thạch, Hai Bà Trưng, Alexandre de Rhodes, Võ Văn Tần, …

Qua tìm hiểu bài học này chúng ta biết được:

Hai đường thẳng song song là hai đường thẳng không có điểm chung.

Hai đường thẳng cắt nhau là hai đường thẳng có một điểm chung.

Do đó, ta có:

Hai đường phố gợi lên hình ảnh hai đường thẳng song song là: Nguyễn Đình Chiểu và Nguyễn Thị Minh Khai.

Hai đường phố gợi lên hình ảnh hai đường thẳng cắt nhau là: Nguyễn Đình Chiểu và Tam Kỳ khởi nghĩa.

Hoạt động Toán 6 bài 2 chương 6

Hoạt động 1

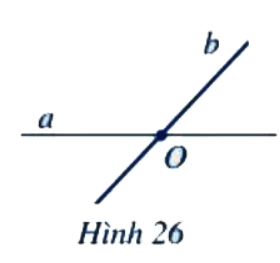
Hai đường thẳng ở Hình 26 có bao nhiêu điểm chung?

Gợi ý đáp án

Hai đường thẳng ở Hình 26 có 1 điểm chung duy nhất là O.

Hoạt động 2

Mỗi bức ảnh sau đây gợi nên hình ảnh về hai đường thẳng. Hai đường thẳng đó có điểm chung không?

Gợi ý đáp án

- Hình ảnh các con đường nhìn từ trên cao là các đường thẳng không có điểm chung.

- Hình ảnh hai đường dây điện trên bầu trời là các đường thẳng không có điểm chung.

Giải bài tập Toán 6 trang 83 tập 2

Câu 1

Quan sát Hình 35, đọc tên hai đường thẳng song song, hai đường thẳng cắt nhau và chỉ ra giao điểm của chúng (nếu có)

Gợi ý đáp án

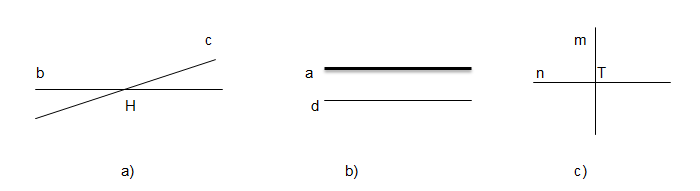
Hai đường thẳng song song là đường thẳng a và d

Hai đường thẳng cắt nhau là đường thẳng b và c (giao điểm là H), n và m (giao điểm là T)

Câu 2

Quan sát Hình 36 và chỉ ra:

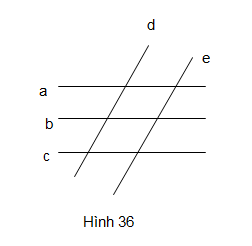
a) Các cặp đường thẳng song song

b) Các cặp đường thẳng cắt nhau

Gợi ý đáp án

a) Các cặp đường thẳng song song: a//b//c ; d//e

b) Các cặp đường thẳng cắt nhau: a cắt d, e; b cắt d, e; c cắt d, e

Câu 3

Quan sát Hình 37. Hãy nêu các cặp đường thẳng cắt nhau và xác định giao điểm của chúng.

Gợi ý đáp án

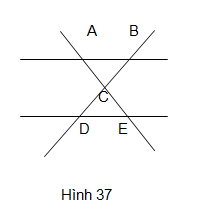
AB cắt AE tại A

AB cắt DB tại B

DE cắt AE tại E

DE cắt DB tại D

AE cắt DB tại C

Câu 4

Cho ba điểm H, I, K thẳng hàng

a) Điểm K có thuộc đường thẳng IH không?

b) Vẽ đường thẳng d đi qua H và không đi qua I. Đường thẳng d có song song với đường thẳng IK không?

Gợi ý đáp án

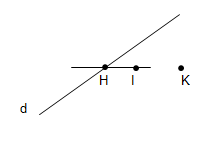
a) K thuộc đường IH

b) Đường thẳng d không song song với đường thẳng IK vì d cắt IK

Câu 5

Cho ba điểm P, Q, R không thẳng hàng. Vẽ các đường thẳng đi qua hai trong ba điểm đã cho

a) Điểm P là giao điểm của hai đường thẳng nào?

b) Chỉ ra các cặp đường thẳng cắt nhau.

Gợi ý đáp án

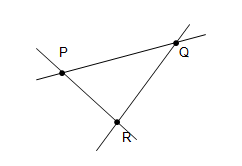
a) P là giao của đường thẳng PQ và PR

b) Các cặp đường thẳng cắt nhau:

PQ và PR

QP và QR

RP và RQ

Câu 6

Vẽ hình theo cách diễn đạt sau:

a) Đường thẳng AB và đường thẳng CD cắt nhau tại I

b) Hai đường thẳng a và b cắt nhau tại O, đường thẳng c cắt a tại P và cắt b tại Q

Gợi ý đáp án

Lý thuyết Toán 6 bài 2 trang 80

I. Hai đường thẳng cắt nhau

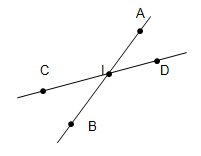
Nếu hai đường thẳng chỉ có một điểm chung, ta nói rằng hai đường thẳng đó cắt nhau. Điểm chung được gọi là giao điểm của hai đường thẳng.

II. Hai đường thẳng song song

- Khái niệm: Hai đường thẳng song song (trong mặt phẳng) là hai đường thẳng không có điểm chung

- Dấu hiệu nhận biết

Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc so le trong bằng nhau thì hai đường thẳng song song
Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc đồng vị bằng nhau thì hai đường thẳng song song
Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc trong cùng phía bù nhau thì hai đường thẳng song song

- Cách vẽ hai đường thẳng song song

Vẽ đường thẳng CD đi qua điểm E và song song với đường thẳng AB cho trước.

Ta có thể vẽ như sau:

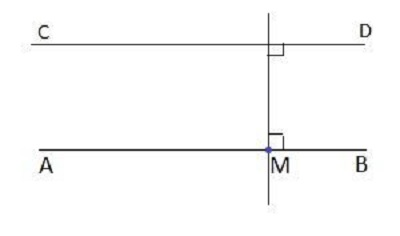
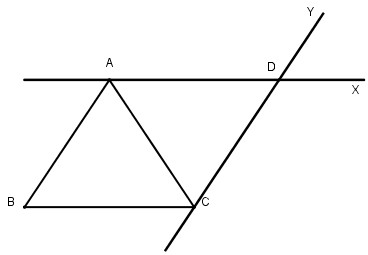
Vẽ đường thẳng MN đi qua điểm E và vuông góc với đường thẳng AB.
Vẽ đường thẳng CD đi qua điểm E và vuông góc với đường thẳng MN ta được đường thẳng CD song song với đường thẳng AB

Ví dụ: Cho hình tam giác ABC có góc đỉnh A là góc vuông. Qua A hãy vẽ đường thẳng AX song song với cạnh BC. Qua C, hãy vẽ đường thẳng CY song song với cạnh AB. Hai đường thẳng AX và CY cắt nhau tại điểm D. Nêu tên các cặp cạnh song song với nhau có trong hình tứ giác ADCB?

Cách giải:

Sử dụng eke để vẽ, ta được tứ giác ADBC như sau:

Trong tứ giác ADBC có: