Toán 6 Bài 2: Xác suất thử nghiệm Giải Toán lớp 6 trang 105 sách Chân trời sáng tạo - Tập 2

Bài trước

Mục lục

Bài sau

Giải Toán lớp 6 Bài 2: Xác suất thử nghiệm bao gồm đáp án chi tiết cho từng phần, từng bài tập trong SGK Toán 6 Tập 2 Chân trời sáng tạo trang 103, 104, 105.

Lời giải Toán 6 Bài 2 Chân trời sáng tạo trình bày khoa học, biên soạn dễ hiểu, giúp các em nâng cao kỹ năng giải Toán 6, từ đó học tốt môn Toán lớp 6 hơn. Đồng thời, cũng giúp thầy cô nhanh chóng soạn giáo án Bài 2 Chương 9: Một số yếu tố xác suất. Mời thầy cô và các em cùng theo dõi bài viết dưới đây của Eballsviet.com:

Giải Toán 6 bài 2: Xác suất thử nghiệm

Giải Toán 6 Chân trời sáng tạo Hoạt động

Hoạt động 1

Trong hộp có 5 quả bóng xanh và 1 quả bóng đỏ. Không nhìn vào hộp, chọn ra từ hộp một quả bóng. Xét các sự kiện sau:

Bóng chọn ra có màu vàng;
Bóng chọn ra không có màu vàng.
Bóng chọn ra có màu xanh.

Sự kiện nào có khả năng xảy ra cao nhất?

Gợi ý đáp án:

- Sự kiện “Bóng chọn ra có màu vàng” không thể xảy ra. Vì trong hộp không có quả bóng màu vàng.

- Sự kiện “Bóng chọn ra không có màu vàng:” chắc chắn xảy ra. Vì trong hộp không có quả bóng màu vàng.

- Trong hộp có cả quả bóng màu xanh và màu đỏ. Khi lấy ra một quả bóng từ trong hộp ra thì có thể lấy được số quả bóng màu xanh hoặc màu đỏ.

Do đó, sự kiện “Bóng chọn ra có màu xanh” có thể xảy ra.

Vậy sự kiện có khả năng xảy ra cao nhất là: “Bóng chọn ra không có màu vàng”.

Hoạt động 2

Thực hiện việc xoay ghim 20 lần quanh trục bút chì và sử dụng bảng kiểm đếm theo mẫu như hình vẽ để đếm số lần ghim chỉ vào mỗi màu.

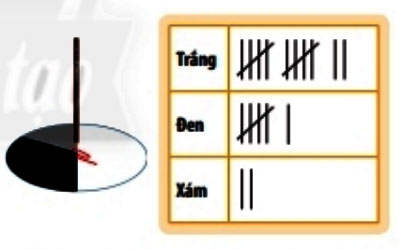
Hoạt động 2

Hãy tính tỉ số của số lần ghim chỉ vào ô màu trắng và tổng số lần xoay ghim.

Gợi ý đáp án:

Tổng số lần xoay ghim là 20 lần.

Số ghim chỉ vào ô màu trắng trong 20 lần xoay là 12 lần.

Tỉ số của số lần ghim chỉ vào ô màu trắng và tổng số lần xoay là:

$12:20 = \frac{{12}}{{20}}$ $12:20 = \frac{{12}}{{20}}$

Vậy tỉ số của số lần ghim chỉ vào ô màu trắng và tổng số lần xoay là $\frac{3}{5}$ $\frac{3}{5}$

Giải Toán 6 Chân trời sáng tạo Thực hành, Vận dụng

Thực hành

Tìm xác suất thực nghiệm của sự kiện ghim chỉ vào ô màu xám, màu đen.

Gợi ý đáp án:

Tổng số lần xoay ghim là 20 lần.

Số ghim chỉ vào ô màu xám trong 20 lần xoay là 2 lần.

Xác suất thực nghiệm của sự kiện ghim chỉ vào ô màu xám là:

$2:20 = \frac{2}{{50}} = \frac{1}{5}$ $2:20 = \frac{2}{{50}} = \frac{1}{5}$

Số ghim chỉ vào ô màu đen trong 20 lần xoay là 6 lần.

Xác suất thực nghiệm của sự kiện ghim chỉ vào ô màu đen là:

$6:20 = \frac{6}{{20}} = \frac{3}{{10}}$ $6:20 = \frac{6}{{20}} = \frac{3}{{10}}$

Vậy xác suất thực nghiệm của sự kiện ghim chỉ vào ô màu xám là $\frac{1}{5}$ $\frac{1}{5}$

Và xác suất thực nghiệm của sự kiện ghim chỉ vào ô màu đen là $\frac{3}{{10}}$ $\frac{3}{{10}}$

Vận dụng

Hằng ngày Sơn đều đi xe buýt đến trường. Sơn ghi lại thời gian chờ xe của mình trong 20 lần liên tiếp ở bảng sau:

Vận dụng

Hãy tính xác suất thực nghiệm của các sự kiện:

a) Sơn phải chờ xe dưới 1 phút.

b) Sơn phải chờ xe từ 5 phút trở lên.

Gợi ý đáp án:

Tổng số lần Sơn chờ xe buýt là:

4 + 10 + 4 + 2 = 20 (lần)

a) Số lần Sơn phải chờ xe dưới 1 phút là 4 (lần)

Xác suất thực nghiệm của sự kiện “Sơn phải chờ xe dưới 1 phút” là:

$4:20 = \frac{4}{{20}} = \frac{1}{5}$ $4:20 = \frac{4}{{20}} = \frac{1}{5}$

Vậy xác suất thực nghiệm của sự kiện “Sơn phải chờ xe dưới 1 phút” là $\frac{1}{5}$ $\frac{1}{5}$

b) Số lần Sơn phải chờ xe từ 5 phút trở lên là tổng số lần Sơn chờ xe từ 5 phút đến 10 phút và từ 10 phút trở lên.

=> Số lần Sơn phải chờ xe từ 5 phút trở lên là:

4 + 2 = 6 (lần)

Xác suất thực nghiệm của sự kiện “Sơn phải chờ xe từ 5 phút trở lên” là:

$6:20 = \frac{6}{{20}} = \frac{3}{{10}}$ $6:20 = \frac{6}{{20}} = \frac{3}{{10}}$

Vậy xác suất thực nghiệm của sự kiện “Sơn phải chờ xe từ 5 phút trở lên” là $\frac{3}{{10}}$ $\frac{3}{{10}}$

Giải Toán 6 Chân trời sáng tạo trang 105 tập 2

Bài 1

Gieo một con xúc sắc 4 mặt 50 lần và quan số ghi trên đỉnh của con xúc ắc, ta được kết quả như sau:

Số xuất hiện	1	2	3	4
Số lần	12	14	15	9

Hãy tính xác suất thực nghiệm để:

a) Gieo được đỉnh số 4

b) Gieo được đỉnh có số chẵn

Gợi ý đáp án:

a) Xác suất thực nghiệm để gieo được đỉnh số 4 là: $\frac{9}{50}$ $\frac{9}{50}$

b) Xác suất thực nghiệm để gieo được đỉnh có số chẵn: $(14+9):50=\frac{23}{50}$ $(14+9):50=\frac{23}{50}$

Bài 2

Trong hộp có một số bút xanh và một số bút đỏ. Lấy ngẫu nhiên 1 bút từ hộp, xem màu rồi trả lại. Lặp lại hoạt động trên 50 lần, ta được kết quả như sau:

Loại bút	Bút xanh	Bút đỏ
Số lần	42	8

a) Tính xác suất thực nghiệm của sự kiện lấy được bút xanh

b) Em hãy dự đoán xem trong hộp loại bút nào có nhiều hơn.

Gợi ý đáp án:

a) Xác suất thực nghiệm của sự kiện lấy được bút xanh là:

$42:50=\frac{21}{25}$ $42:50=\frac{21}{25}$

b) Dự đoán: Trong hộp loại bút xanh có nhiều hơn.

Bài 3

Tổng hợp kết quả xét nghiệm bệnh viêm gan ở một phòng khám trong một năm, ta được bảng sau:

Quý	Số ca xét nghiệm	Số ca dương tính
I	150	15
II	200	21
II	180	17
IV	220	24

Hãy tính xác suất thực hiện của sự kiện một ca xét nghiệm có kết quả dương tính.

a) theo từng quý trong năm.

b) sau lần lượt từng quý tính từ đầu năm.

Gợi ý đáp án:

a) Xác suất thực hiện một ca xét nghiệm có kết quả dương tính theo từng quý là:

Quý I: $15:150=\frac{1}{10}$ $15:150=\frac{1}{10}$

Quý II: $21:200=\frac{21}{200}$ $21:200=\frac{21}{200}$

Quý III: $17:180=\frac{17}{180}$ $17:180=\frac{17}{180}$

Quý IV: $24:220=\frac{6}{55}$ $24:220=\frac{6}{55}$

b) sau lần lượt từng quý tính từ đầu năm

Quý I: $15:750=\frac{1}{50}$ $15:750=\frac{1}{50}$

Quý II: $21:750=\frac{7}{250}$ $21:750=\frac{7}{250}$

Quý III: $17:750=\frac{17}{750}$ $17:750=\frac{17}{750}$

Quý IV: $24:750=\frac{12}{375}$ $24:750=\frac{12}{375}$

Lý thuyết Xác suất thực nghiệm

1. Khả năng xảy ra của một sự kiện

Khi thực hiện một phép thử nghiệm, một sự kiện có thể xảy ra hoặc không thể xảy ra. Để nói về khả năng xảy ra của mỗi sự kiện, ta dùng một con số có giá trị từ 0 đến 1.

Một sự kiện không thể xảy ra có khả năng xảy ra bằng 0.

Một sự kiện chắc chắn xảy ra có khả năng xảy ra bằng 1.

Ví dụ 1. Trong hộp có 3 quả bóng: bóng xanh, bóng đỏ và bóng vàng. Không nhìn vào hộp, chọn ra từ hộp một quả bóng. Xét khả năng xảy ra của mỗi sự kiện sau:

a) Bóng chọn ra có một trong ba quả: bóng xanh, bóng đỏ hoặc bóng vàng;

b) Bóng chọn ra có màu tím.

Lời giải:

a) Khi chọn một quả bóng từ hộp thì quả bóng được chọn ra có một trong ba quả: bóng xanh, bóng đỏ hoặc bóng vàng.

Do đó, sự kiện này chắc chắn xảy ra.

Vậy sự kiện “Bóng chọn ra có một trong ba quả: bóng xanh, bóng đỏ hoặc bóng vàng” có khả năng xảy ra bằng 1.

b) Vì ba quả trong hộp không có quả bóng nào có màu tím nên sự kiện “Bóng chọn ra có màu tím” không xảy ra.

Vậy sự kiện “Bóng chọn ra có màu tím” có khả năng xảy ra bằng 0.

2. Xác suất thực nghiệm

Thực hiện lặp đi lặp lại một hoạt động nào đó n lần. Gọi n(A) là số lần sự kiện A xảy ra trong n lần đó. Tỉ số $\frac{n\left(A\right)}{n}$ $\frac{n\left(A\right)}{n}$ = Số lần sự kiện A xảy ra : Tổng số lần thực hiện hoạt động được gọi là xác suất thực nghiệm của sự kiện A sau n hoạt động vừa thực hiện.

Chia sẻ bởi: