Toán 6 Bài 9: Ước và bội Giải Toán lớp 6 trang 30 - Tập 1 sách Chân trời sáng tạo

Giới thiệu Tải về Bình luận

Giải bài tập Toán lớp 6 Bài 9: Ước và bội với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán 6 Tập 1 Chân trời sáng tạo trang 28, 29, 30. Qua đó, giúp các em ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán.

Giải Toán 6 Bài 9 chi tiết, còn giúp các em hệ thống lại toàn bộ kiến thức lý thuyết trọng tâm của Bài 9 Chương 1: Số tự nhiên. Bên cạnh đó, cũng giúp thầy cô soạn giáo án cho học sinh của mình. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Eballsviet.com:

Giải Toán 6 bài 9: Ước và bội Chân trời sáng tạo

Phần Hoạt động khởi động

Ước và bội có họ hàng với nhau không nhỉ?

Đáp án

Sau bài học này ta thấy ước và bội có quan hệ với nhau như sau:

a là ước của b thì b là bội của a.

Phần Hoạt động khám phá

Hoạt động 1 trang 28 Toán 6 tập 1

a) Lớp 6A có 36 học sinh. Trong một tiết mục đồng diễn thể dục nhịp điệu, lớp xếp thành đội hình gồm những hàng đều nhau. Hãy hoàn thành bảng sau vào vở để tìm các cách mà lớp có thể xếp đội hình

Cách xếp đội hình	Số hàng	Số học sinh trong một hàng
Thứ nhất	1	36
Thứ hai	2	18
...	...	...
...	...	...

b) Viết số 36 thành tích của hai số bằng các cách khác nhau.

Đáp án

Cách xếp đội hình	Số hàng	Số học sinh trong một hàng
Thứ nhất	1	36
Thứ hai	2	18
Thứ ba	3	12
Thứ tư	4	9
Thứ năm	6	6

b) 36 = 1 . 36

36 = 2 . 18

36 = 3 . 12

36 = 4 . 9

36 = 6 . 6

Hoạt động 2 trang 29 Toán 6 tập 1

Số 18 có thể chia hết cho những số nào?

Đáp án

Số 18 có thể chia hết cho các số 1, 2, 3, 6, 9, 18.

Hoạt động 3 trang 29 Toán 6 tập 1

a) Chuẩn bị một số mảnh giấy nhỏ có chiều dài 3 cm. Ghép các mảnh giấy nhỏ đó thành các băng giấy như minh họa dưới đây:

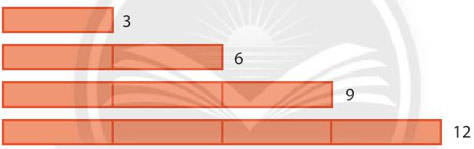
Hoạt động 3

Độ dài băng giấy đầu tiên là: 3.1 = 3 (cm);

Độ dài băng giấy thứ hai là: 3.2 = 6 (cm);

Tiếp tục cách đó, ta có thể tính độ dài các băng giấy thứ ba, thứ tư lần lượt là:

3.3 = 9 (cm); 3.4 = 12 (cm);

…

- Hãy tính độ dài của hai băng giấy tiếp theo.

- Nêu nhận xét về mối liên hệ giữa số đo độ dài (cm) của các băng giấy nói trên với 3.

b) Làm thế nào để tìm được các bội của 3 một cách nhanh chóng?

Đáp án

a) – Độ dài của miếng băng tiếp theo là: 3 . 5 = 15 (cm).

– Các số đo dài của các băng giấy là các bội của 3.

b) Muốn tìm bội của 3 một cách nhanh chóng, ta nhân 3 lần lượt với 0, 1, 2, 3,…

Phần Thực hành

Thực hành 1 trang 28 Toán 6 tập 1

1) Chọn từ thích hợp trong các từ “ước”, “bội” thay thế ? ở mỗi câu sau để có khẳng định đúng.

a) 48 là ? của 6;

b) 12 là ? của 48;

c) 48 là ? của 48;

d) 0 là ? của 48.

2) Hãy chỉ ta các ước của 6.

3) Số 24 là bội của những số nào?

Gợi ý đáp án:

1) a) 48 là bội của 6

b) 12 là ước của 48

c) 48 là ước/bội của 48

d) 0 là bội của 48

2) Ư(6) = {1; 2; 3; 6}.

3) Ư(24) = {1;2;3;4;6;8;12;24}.

=> Số 24 là bội của 1, 2, 3, 4, 6, 8, 12, 24.

Thực hành 2 trang 29 Toán 6 tập 1

Hãy tìm các tập hợp sau:

a) Ư(17)

b) Ư(20)

Gợi ý đáp án:

a) Ư(17) = {1; 17}.

b) Ư(20) = { 1; 2; 4; 5; 10; 20}.

Thực hành 3 trang 30 Toán 6 tập 1

Hãy tìm các tập hợp sau

a) B(4)

b) B(7)

Gợi ý đáp án:

a) B(4) = {0, 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44,…}.

b) B(7) = {0, 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77,…}.

Phần Bài tập

Bài 1 trang 30 Toán 6 tập 1

Chọn kí hiệu ∈ hoặc ∉ thay cho “?” trong mỗi câu sau để được các kết luận đúng.

a) 6 ? Ư(48);

d) 18 ? B(4);

b) 12 ? Ư(30);

e) 28 ? B(7);

c) 7 ? Ư(42);

f) 36 ? B(12).

Gợi ý đáp án:

a) 6 ∈ Ư(48)

d) 18 ∉ B(4)

b) 12 ∉ Ư(30)

e) 28 ∈ B(7)

c) 7 ∈ Ư(42)

f) 36 ∈ B(12)

Bài 2 trang 30 Toán 6 tập 1

a) Tìm tập hợp các ước của 30;

b) Tìm tập hợp các bội của 6 nhỏ hơn 50;

c) Tìm tập hợp C các số tự nhiên x sao cho x vừa là bội của 18, vừa là ước của 72.

Gợi ý đáp án:

a) Ư(30) = {1; 2; 3; 5; 6; 15; 30}.

b) B(6) = {0; 6; 12; 18; 24; 30; 36; 42; 48}.

c) C = {18; 36; 72}.

Bài 3 trang 30 Toán 6 tập 1

Viết mỗi tập hợp sau bằng cách liệt kê các phần tử.

a) A = {x ∈ Ư(40) | x > 6};

b) B = {x ∈ B(12) | 24 ≤ x ≤ 60}.

Gợi ý đáp án:

a) A = {8;10; 20; 40}.

b) B = {24; 36;48;60}.

Bài 4 trang 30 Toán 6 tập 1

Trò chơi “Đua viết số cuối cùng" Bình và Minh chơi trò chơi “đua viết số cuối cùng". Hai bạn thi viết các số theo luật như sau: Người chơi thứ nhất sẽ viết một số tự nhiên không lớn hơn 3. Sau đó đến lượt người thứ hai viết rồi quay lại người thứ nhất và cứ thế tiếp tục, ... sao cho kể từ sau số viết đầu tiên, mỗi bạn viết một số lớn hơn số bạn mình vừa viết nhưng không lớn hơn quá 3 đơn vị. Ai viết được số 20 trước thì người đó thắng. Sau một số lần chơi, Minh thấy Bình luôn thắng. Minh thắc mắc: “Sao lúc nào cậu cũng thắng tớ thế?". Bình cười: “Không phải lúc nào tớ cũng thắng được cậu đâu".

a) Bình đã chơi như thế nào để thắng được Minh? Minh có thể thắng được Bình khi nào?

b) Hãy chơi cùng bạn trò chơi trên. Em hãy đề xuất một luật chơi mới cho trò chơi trên rồi chơi cùng các bạn.

Gợi ý đáp án:

a) Bình đã áp dụng cách tìm bội của một số để để thắng được Minh. Cụ thể là Bình đã áp dụng để tính các bội của 3 rồi viết lần lượt các bội của 3 khi chơi trò chơi với Minh.

b) Đề xuất luật chơi mới: Người chơi thứ nhất sẽ viết một số tự nhiên không lớn hơn 5. Sau đó đến lượt người thứ hai viết rồi quay lại người thứ nhất và cứ thế tiếp tục, ... sao cho kể từ sau số viết đầu tiên, mỗi bạn viết một số lớn hơn số bạn mình vừa viết nhưng không lớn hơn quá 5 đơn vị.

=> Ta sẽ tính các bội của 5 rồi viết lần lượt các bội của 5 khi chơi trò chơi.

Em có biết?

Theo dương lịch, một năm thường có 365 ngày, riêng năm nhuận có thêm 1 ngày và ngày đó được cố định là ngày 29 tháng Hai. Thông thường, năm nhuận có số năm là bội của 4. Các năm 2044, 2086 có phải năm nhuận không?

Gợi ý đáp án:

2044 là bội của 4 nên năm 2044 là năm nhuận

2086 không là bội của 4 nên năm 2086 không phải năm nhuận

Lý thuyết Toán 6 Bài 9: Ước và bội

1. Ước và bội

Nếu có số tự nhiên a chia hết cho số tự nhiên b thì ta nói a là bội của b, còn b là ước của a.

Ví dụ: Ta có 12 ⋮ 6.

Khi đó, 12 là bội của 6, còn 6 là ước của 12.

Tập hợp các ước của a được kí hiệu là Ư(a). Tập hợp các bội của a được kí hiệu là B(a).

Ví dụ: Ư(8) = {1; 2; 4; 8}; B(5) = {0; 5; 10; 15; 20; …}.

Chú ý:

- Số 0 là bội của tất cả các số tự nhiên khác 0. Số 0 không là ước của bất kì số tự nhiên nào.

- Số 1 chỉ có một ước là 1. Số 1 là ước của mọi số tự nhiên.

- Mọi số tự nhiên a lớn hơn 1 luôn có ít nhất hai ước là 1 và chính nó.

2. Cách tìm ước

Cách tìm Ư(a):

Ta có thể tìm các ước của a (a > 1), ta có thể lần lượt chia a cho các số tự nhiên từ 1 đến a để xét xem a chia hết cho những số nào, khi đó các số ấy là ước của a.

Ví dụ:

Ta có 16 : 1 = 16; 16 : 2 = 8; 16 : 4 = 4; 16 : 8 = 2; 16 : 16 = 1.

Do đó các ước của 16 là: 1; 2; 4; 8; 16.

Vậy tập hợp các ước của 16 là: Ư(16) = {1; 2; 4; 8; 16}.

3. Cách tìm bội

Cách tìm B (a):

Muốn tìm bội của số tự nhiên a khác 0, ta có thể nhân a lần lượt với 0, 1, 2, 3, ...

Chú ý:

Bội của a có dạng tổng quát là a.k với k∈ℕ. Ta có thể viết:

B(a) = {a.k|k∈ℕ}.

Ví dụ:

Ta có: 6 . 0 =0; 6 . 1 = 6; 6 . 2 = 12; 6 . 3 = 18; …