Toán 6 Bài tập cuối chương 7 - Chân trời sáng tạo Giải Toán lớp 6 trang 67, 68 - Tập 2

Giải Toán lớp 6 Bài tập cuối chương 7 bao gồm đáp án chi tiết cho từng phần, từng bài tập trong SGK Toán 6 Tập 2 Chân trời sáng tạo trang 67, 68.

Lời giải Toán 6 Chân trời sáng tạo trình bày khoa học, biên soạn dễ hiểu, giúp các em nâng cao kỹ năng giải Toán 6, từ đó học tốt môn Toán lớp 6 hơn. Đồng thời, cũng giúp thầy cô nhanh chóng soạn giáo án Bài tập cuối chương 7: Hình học trực quan - Tính đối xứng của hình phẳng trong thế giới tự nhiên. Mời thầy cô và các em cùng theo dõi bài viết dưới đây của Eballsviet.com:

Giải câu hỏi Trắc nghiệm Chân trời sáng tạo trang 67 tập 2

Quan sát các chữ cái H A N O I và xác định đúng, sai cho các phát biểu sau:

a) Chữ H là hình vừa có trục đối xứng, vừa có tâm đối xứng.

b) Chữ A là hình có trục đối xứng và không có tâm đối xứng.

c) Chữ N là hình có trục đối xứng và có tâm đối xứng.

d) Chữ O là hình vừa có trục đối xứng vừa có tâm đối xứng.

e) Chữ I là hình có trục đối xứng và không có tâm đối xứng.

Gợi ý đáp án:

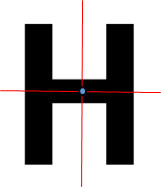
a) Chữ H là hình vừa có trục đối xứng, vừa có tâm đối xứng là phát biểu đúng.

Trục đối xứng và tâm đối xứng của chữ H được biểu diễn như hình vẽ.

b) Chữ A là hình có trục đối xứng và không có tâm đối xứng là phát biểu đúng.

Trục đối xứng của chữ A được biểu diễn như hình vẽ.

c) Chữ N là hình có trục đối xứng và có tâm đối xứng là phát biểu sai. Vì chữ N không có trục đối xứng và có tâm đối xứng.

Trục đối xứng của chữ N được biểu diễn như hình vẽ.

d) Chữ O là hình vừa có trục đối xứng vừa có tâm đối xứng là phát biểu đúng.

Trục đối xứng và tâm đối xứng của chữ O được biểu diễn như hình vẽ.

e) Chữ I là hình có trục đối xứng và không có tâm đối xứng là phát biểu sai.

Vì chữ I là hình vừa có trục đối xứng vừa có tâm đối xứng.

Trục đối xứng và tâm đối xứng của chữ I được biểu diễn như hình vẽ.

Vậy trong các phát biểu trên, các phát biểu a), b), d) đúng. Phát biểu c), e) sai.

Giải Toán 6 Chân trời sáng tạo trang 68 tập 2

Bài 1

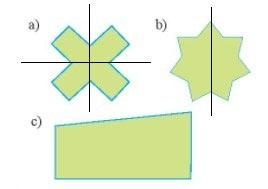
Các đường nét đứt ở mỗi hình bên dưới có phải là trục đối xứng không?

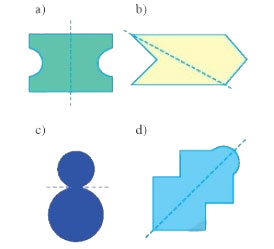
Gợi ý đáp án:

- Hình a) có đường nét đứt là trục đối xứng. Vì khi gấp hình theo đường nét đứt thì được hai nửa hình chồng khít lên nhau.

- Hình b) có đường nét đứt không phải là trục đối xứng. Vì khi gấp hình theo đường nét đứt thì được hai nửa hình không chồng khít lên nhau.

- Hình c) có đường nét đứt không phải là trục đối xứng. Vì khi gấp hình theo đường nét đứt thì được hai nửa hình không chồng khít lên nhau.

- Hình d) có đường nét đứt là trục đối xứng. Vì khi gấp hình theo đường nét đứt thì được hai nửa hình chồng khít lên nhau.

Bài 2

Em hãy vẽ các hình sau vào vở rồi tô màu các ô vuông để mỗi hình thu được nhận đường nét đứt là trục đối xứng.

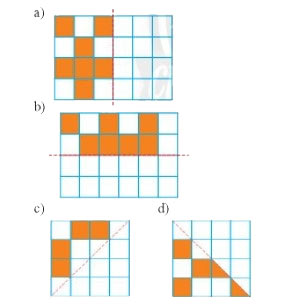
Gợi ý đáp án:

a) Bước 1: Chọn một ô vuông bất kỳ trên hình. Giả sử ta chọn ô vuông số 1 (như hình vẽ).

Bước 2: Tìm ô vuông đối xứng với ô vuông số 1 qua đường nét đứt rồi tô màu ô vuông đó (như hình vẽ)

Bước 3: Tiếp tục tô màu các ô vuông đối xứng với ô vuông ở nửa hình bên trái qua đường nét đứt, ta được hình mới nhận đường nét đứt làm trục đối xứng (như hình vẽ).

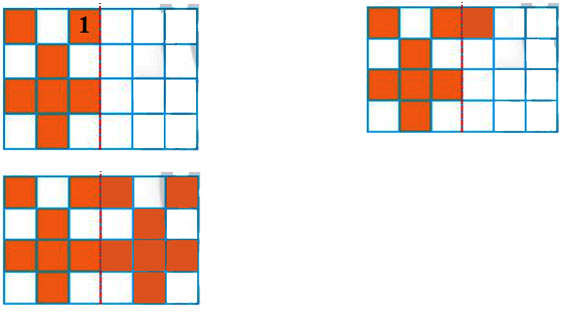
b) Bước 1: Chọn một ô vuông bất kỳ trên hình. Giả sử ta chọn ô vuông số 1 (như hình vẽ).

Bước 2: Tìm ô vuông đối xứng với ô vuông số 1 qua đường nét đứt rồi tô màu ô vuông đó (như hình vẽ).

Bước 3: Tiếp tục tô màu các ô vuông đối xứng với ô vuông ở nửa hình bên trái qua đường nét đứt, ta được hình mới nhận đường nét đứt làm trục đối xứng (như hình vẽ).

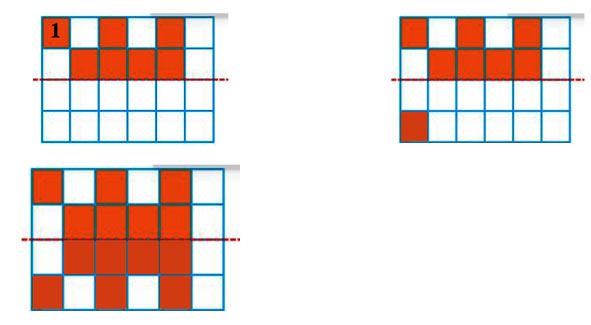
c) Bước 1: Chọn một ô vuông bất kỳ trên hình. Giả sử ta chọn ô vuông số 1 (như hình vẽ).

Bước 2: Tìm ô vuông đối xứng với ô vuông số 1 qua đường nét đứt rồi tô màu ô vuông đó (như hình vẽ).

Bước 3: Tiếp tục tô màu các ô vuông đối xứng với ô vuông ở nửa hình bên trái qua đường nét đứt, ta được hình mới nhận đường nét đứt làm trục đối xứng (như hình vẽ).

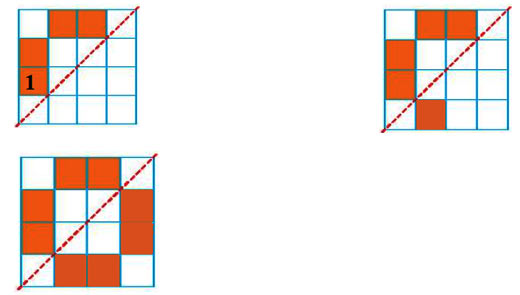
d) Bước 1: Chọn một ô vuông bất kỳ trên hình. Giả sử ta chọn ô vuông số 1 (như hình vẽ).

Bước 2: Tìm ô vuông đối xứng với ô vuông số 1 qua đường nét đứt rồi tô màu ô vuông đó (như hình vẽ).

Bước 3: Tiếp tục tô màu các ô vuông đối xứng với ô vuông ở nửa hình bên trái qua đường nét đứt, ta được hình mới nhận đường nét đứt làm trục đối xứng (như hình vẽ).

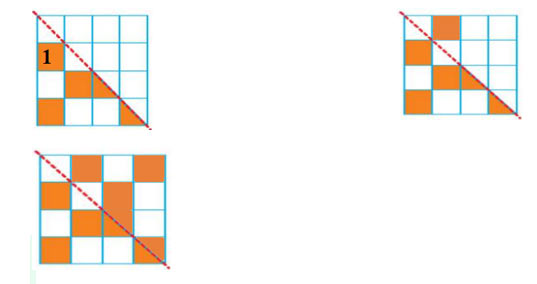
Bài 3

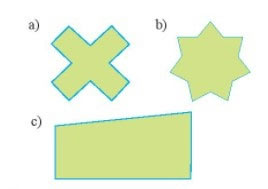
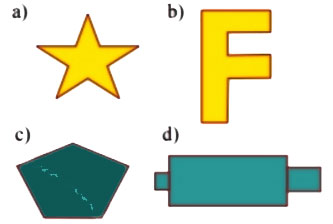
Hình nào sau đây có tâm đối xứng? Hình nào vừa có tâm đối xứng vừa có trục đối xứng?

Gợi ý đáp án:

Hình b có trục đối xứng. Hình a vừa có tâm đối xứng, vừa có trục đối xứng.

Bài 4

Hình nào sau đây có trục đối xứng?

Gợi ý đáp án:

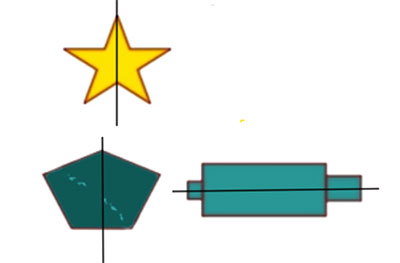
Nhận xét: Hình a) có trục đối xứng (như hình vẽ)

Hình b) không có trục đối xứng.

Hình c) có trục đối xứng (như hình vẽ)

Hình d) có trục đối xứng (như hình vẽ)

Vậy hình a), hình c) và hình d) có trục đối xứng.

Bài 5

Hai bạn Na và Toàn đứng đối diện nhau trên nền đất, ở giữa họ có một dãy các số và dấu cộng như hình dưới đây. Do vị trí khác nhau nên hai bạn thấy hai dãy phép tính khác nhau.

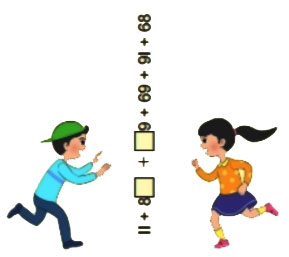
Hãy tìm cách điền hai chữ số vào hai ô trống để kết quả tính của hai bạn Na và Toàn bằng nhau.

Em nhận xét gì về hình ảnh mà hai bạn quan sát được.

Gợi ý đáp án:

Ở vị trí của mỗi bạn sẽ nhìn thấy các phép tính khác nhau.

- Ở vị trí của Toàn nhìn thấy phép tính:

89 + 16 + 69 + 6… + …8 + 11.

= 6… + …8 + 89 + 16 + 69 + 11 (Tính chất giao hoán)

= (6… + …8) + (89 + 16 + 69 + 11) (Tính chất kết hợp)

= 6… + …8 + 185.

- Ở vị trí của Na nhìn thấy phép tính:

11 + 8… + …9 + 69 + 91 + 68

= 8… + …9 + 11 + 69 + 91 + 68 (Tính chất giao hoán)

= (8… + …9) + (11 + 69 + 91 + 68) (Tính chất kết hợp)

= 8… + …9 + 239.

Để kết quả tính của hai bạn Na và Toàn bằng nhau thì:

6… + …8 + 185 = 8… + …9 + 239

6… + …8 − 8… - …9 = 54

Gọi các ô trống thứ nhất, thứ hai, thứ ba và thứ tư lần lượt là a, b, c, d.

Như trên hình, ta thấy khi quay ngược số a sẽ được số d và quay ngược số b ra số c.

Ta có biểu thức sau:

\(\overline {6a} + \overline {b8} - \overline {8c} - \overline {d9} = 54\)

60 + a + 10b + 8 − (80 + c) − (10d + 9) = 54

60 + a + 10b + 8 − 80 − c − 10d − 9 = 54

a + 10b − c − 10d − 21 = 54

(a + 10b) − (c + 10d) = 75

\(\overline {ba} - \overline {dc} = 75\)

Trong hình vẽ trên, khi quay về phía mỗi bạn thì đều nhận được một phép tính có nghĩa.

Do đó, các chữ số a, b, c, d khi quay ngược lại vẫn tạo ra một số có nghĩa nên a, b, c, d và số 0 không được đứng đầu.

Do đó a, b, c, d

Trường hợp 1: a > c

Khi đó, a − c = 5 và b − d = 7.

- Số a, c thỏa mãn a − c = 5 và a, c nên a = 6; c = 1.

- Số b, d thỏa mãn b − d = 7 và a, c nên b = 8; d = 1.

Nhận thấy: quay ngược số a không ra được số d và quay ngược số b không ra được số c.

Do đó trường hợp này vô lý.

Trường hợp 1: a < c

Khi đó, 10 + a − c = 5 và b − d = 8 hay c − a = 5 và b − d = 8.

(a không trừ được cho c, mượn 10 đơn vị (hay 1 chục) ta có: 10 + a − c = 5, trả 1 vào hàng chục ta có: c − a = 5).

- Số a, c thỏa mãn c − a = 5 và a, c nên c = 6; a = 1.

- Số b, d thỏa mãn b − d = 8 và b, d nên b = 9; d = 1.

Nhận thấy: quay ngược số a ra được số d và quay ngược số b ra được số c.

Do đó trường hợp này thỏa mãn.

Từ đó suy ra, a = 1; b = 9; c = 6; d = 9.

Vậy phép tính cần điền là:

89 + 16 + 69 + 61 + 98 + 11 = 11 + 86 + 19 + 69 + 91 + 68

Hình ảnh mà hai bạn quan sát được là với mỗi số hạng, Na nhìn thấy chữ số ở hàng đơn vị thì Toàn nhìn thấy chữ số quay ngược lại ở hàng chục và ngược lại.

Bài 6

Hãy tìm dụng cụ học tập có tính đối xứng.

Gợi ý đáp án:

- Thước kẻ có trục đối xứng (không tính những khoảng cách ghi trên thân thước).

- Quyển sách có trục đối xứng.

- Bút kéo thủ công có trục đối xứng

- Bút chì có trục đối xứng (không tính các chữ ghi trên thân bút).