Bộ đề thi học kì 1 môn Toán lớp 9 năm 2024 - 2025 (Sách mới) 4 Đề thi cuối kì 1 Toán 9 sách KNTT, CD, CTST (Có ma trận, đáp án)
Đề thi học kì 1 môn Toán 9 năm 2024 - 2025 gồm 4 đề kiểm tra có đáp án chi tiết kèm theo bảng ma trận đề thi.
Đề thi cuối kì 1 Toán 9 gồm 3 sách Cánh diều, Chân trời sáng tạo, Kết nối tri thức được biên soạn với cấu trúc đề rất đa dạng, bám sát nội dung chương trình học trong sách giáo khoa. Hi vọng đây sẽ là tài liệu hữu ích cho quý thầy cô và các em ôn tập và củng cố kiến thức, chuẩn bị sẵn sàng cho học kì 1 lớp 9 sắp tới. Vậy sau đây là nội dung chi tiết TOP 4 đề thi cuối kì 1 Toán 9 năm 2024 - 2025, mời các bạn cùng theo dõi tại đây. Bên cạnh đó các bạn xem thêm đề thi học kì 1 môn Ngữ văn 9, đề thi học kì 1 môn tiếng Anh 9.
Bộ đề thi học kì 1 Toán 9 năm 2024 - 2025 (Sách mới)
1. Đề thi học kì 1 Toán 9 Chân trời sáng tạo






.............
Tải file tài liệu để xem thêm đầy đủ Đề thi học kì 1 Toán 9 Chân trời sáng tạo
2. Đề thi học kì 1 Toán 9 Kết nối tri thức





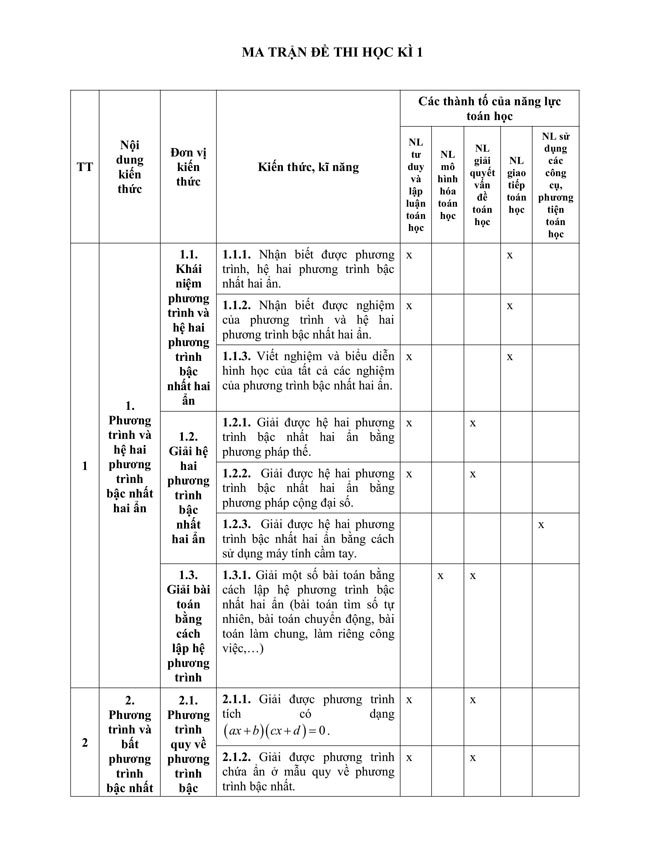
...........
Tải file tài liệu để xem thêm Đề thi học kì 1 Toán 9 Kết nối tri thức
3. Đề thi học kì 1 Toán 9 Cánh diều

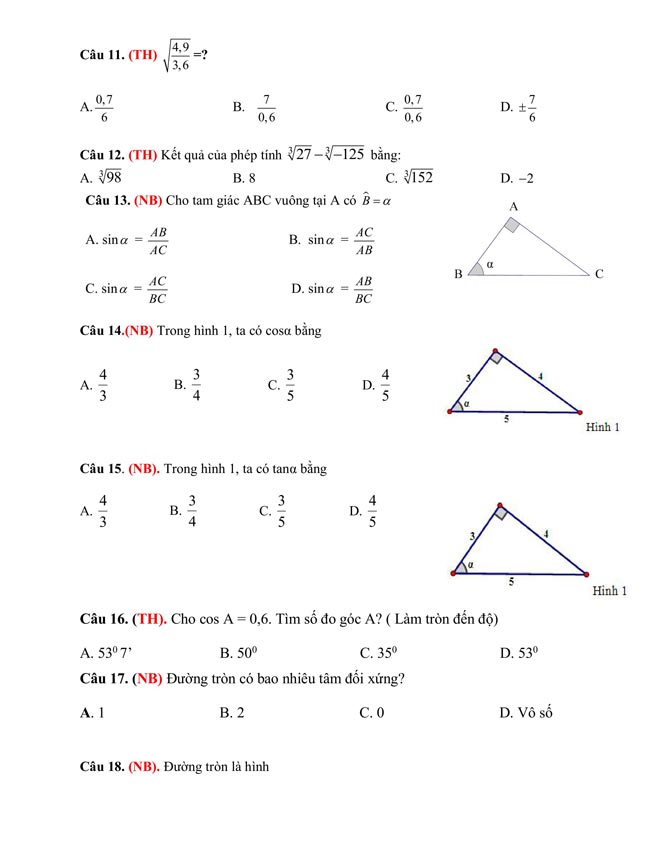


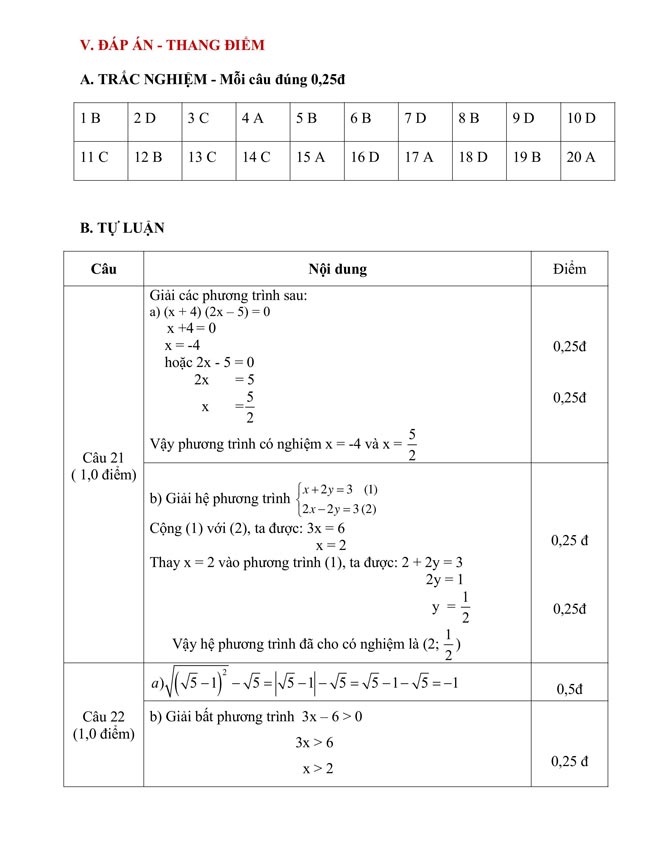
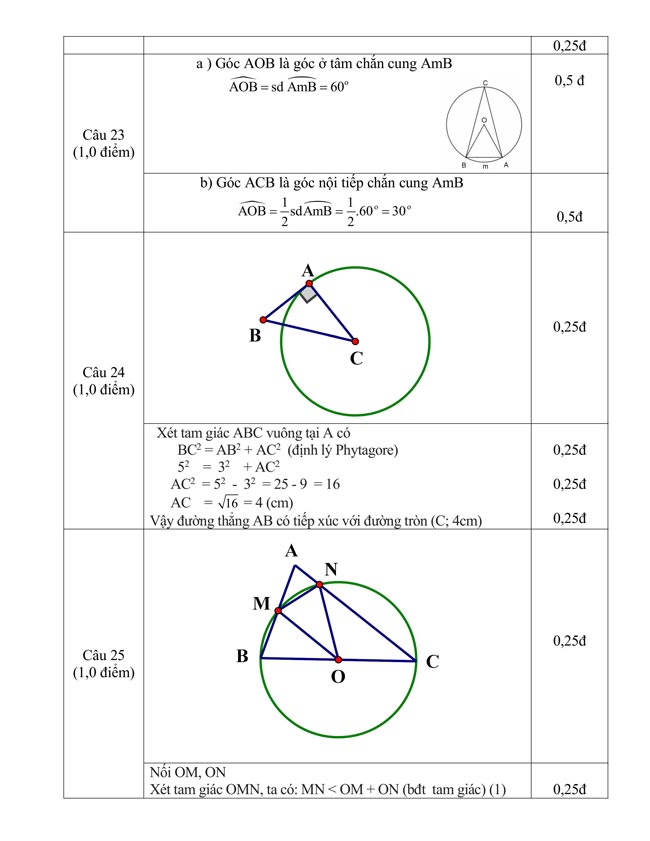
..........
Tải file tài liệu để xem thêm đề thi học kì 1 Toán 9 Cánh diều
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:












 Đề thi giữa kì 2 lớp 9
Đề thi giữa kì 2 lớp 9
 Đề thi học kì 2 Lớp 9
Đề thi học kì 2 Lớp 9
 Đề thi giữa kì 1 lớp 9
Đề thi giữa kì 1 lớp 9
 Đề thi học kì 1 Lớp 9
Đề thi học kì 1 Lớp 9
 Toán 9
Toán 9
 Toán 9 Kết nối tri thức
Toán 9 Kết nối tri thức
 Toán 9 Cánh Diều
Toán 9 Cánh Diều
 Toán 9 Chân trời sáng tạo
Toán 9 Chân trời sáng tạo
 Văn 9 Kết nối tri thức
Văn 9 Kết nối tri thức









