Toán 9 Bài 2: Tiếp tuyến của đường tròn Giải Toán 9 Chân trời sáng tạo tập 1 trang 83 → 89

Giải Toán 9 Bài 2: Tiếp tuyến của đường tròn là tài liệu vô cùng hữu ích giúp các em học sinh lớp 9 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 9 Chân trời sáng tạo tập 1 trang 83, 84, 85, 86, 87, 88, 89.

Giải bài tập Toán 9 Chân trời sáng tạo tập 1 trang 83 → 89 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh ôn tập Bài 2 Chương V: Đường tròn - Phần Hình học và đo lường - Hình học phẳng. Mời thầy cô và các em theo dõi bài viết dưới đây của Eballsviet.com:

Giải Toán 9 Chân trời sáng tạo Tập 1 trang 88, 89

Bài 1

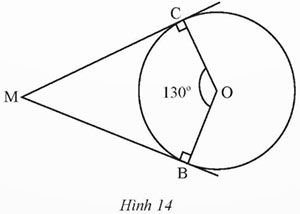
Trong Hình 14, MB, MC lần lượt là tiếp tuyến của đường tròn (O) tại B, C; \(\widehat {COB} =130^{\circ}\). Tính số đo \(\widehat {CMB}\)

Hướng dẫn giải:

Ta có MB và MC là hai tiếp tuyến của đường tròn (O) tại B và C

Suy ra MC ⊥ OC và MB ⊥ OB

Xét tứ giác OBMC, ta có:

\(\widehat{O} + \widehat B + \widehat C + \widehat M=360^{\circ}\)

Suy ra \(\widehat {CMB} =50^{\circ}\)

Bài 2

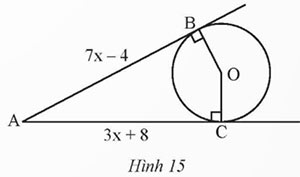
Quan sát Hình 15. Biết AB, AC lần lượt là tiếp tuyến của đường tròn (O) tại B, C. Tính giá trị của x.

Hướng dẫn giải:

Ta có: MA ⊥ OA tại A và MB ⊥ OB tại B

suy ra MA và MB là hai tiếp tuyến với (O) tại A và B

Do đó AB = AC

Suy ra 7x - 4 = 3x + 8

4x = 12

Vậy x = 3.

Bài 3

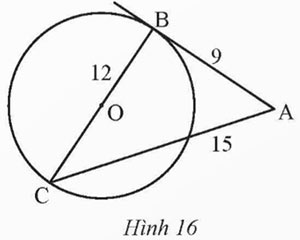
Trong Hình 16, AB = 9, BC = 12, AC = 15 và BC là đường kính của đường tròn (O). Chứng minh AB là tiếp tuyến của đường tròn (O).

Hướng dẫn giải:

Xét tam giác ABC có:

AB² + BC² = 9² + 12² = 225 = 15² = AC²

Do đó tam giác ABC vuông tại B (định lí Pythagore đảo)

Suy ra AB ⊥ BC hay AB ⊥ OB

Xét đường tròn (O) có AB ⊥ OB tại B thuộc (O) nên AB là tiếp tuyến của (O).

Bài 4

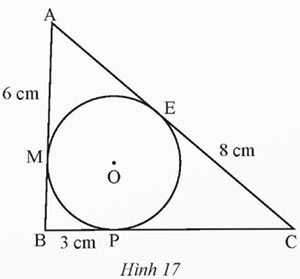
Cho tam giác ABC có đường tròn (O) nằm trong và tiếp xúc với ba cạnh của tam giác. Biết AM = 6 cm, BP = 3 cm, CE = 8 cm (Hình 17). Tính chu vi tam giác ABC.

Hướng dẫn giải:

Ta có: AB, BC, AC lần lượt tiếp xúc với đường tròn (O) tại M, P, E nên AB, BC, AC lần lượt là các tiếp tuyến của (O) tại M, P, E

Giao điểm A của hai tiếp tuyến AB và AC cách đều hai tiếp điểm M và E nên MA = ME

Giao điểm B của hai tiếp tuyến AB và BC cách đều hai tiếp điểm M và P nên MB = BP

Giao điểm C của hai tiếp tuyến BC và AC cách đều hai tiếp điểm E và P nên CE = CP

Vậy chu vi tam giác ABC là:

2AM + 2EC + 2BP = 2 . (6 + 8 + 3) = 34 cm

Bài 5

Cho đường tròn (O; R) có đường kính AB. Vẽ dây AC sao cho AC = R. Gọi I là trung điểm của dây AC. Đường thẳng OI cắt tiếp tuyến Ax tại M. Chứng minh rằng:

a) \(\widehat{ACB}\) có số đo bằng 90^o, từ đó suy ra độ dài của BC theo R

b) OM là tia phân giác của \(\widehat{COA}\)

c) MC là tiếp tuyến của đường tròn (O; R)

Hướng dẫn giải:

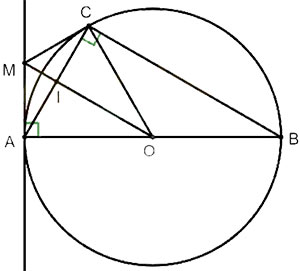
a) Xét tam giác ABC ta có:

CO là đường trung tuyến

OA = OB = OC = R

Do đó tam giác ABC vuông tại C hay \(\widehat{ACB} =90^{\circ}\)

Áp dụng định lí Pythagore trong tam giác vuông ABC, ta có:

AC² + BC² = AB²

Suy ra BC² = AB² - AC² = (2R)² - R² = 3R² hay BC = \(R\sqrt{3}\)

b) Tam giác OAC cân tại O (vì OA = OC = R)

I là trung điểm của AC nến OI là đường trung tuyến đồng thời là tia phân giác của \(\widehat{COA}\)

Suy ra OM là tia phân giác của \(\widehat{COA}\)

c) Xét tam giác vuông AMO và tam giác vuông CMO có:

OA = OC

\(\widehat{AOM}=\widehat{COM}\) (OM là tia phân giác của \(\widehat{COA}\))

OM cạnh chung

Do đó, Δ AMO = Δ CMO (c - g - c)

Suy ra \(\widehat{OAM}=\widehat{OCM}\) (hai góc tương ứng)

Mà Ax là tiếp tuyến của (O) tại A nên \(\widehat{OAM}=90^{\circ}\) hay \(\widehat{OCM}=90^{\circ}\)

Ta có MC ⊥ OC tại C thuộc đường tròn (O) nên MC là tiếp tuyến của đường tròn (O; R).

Bài 6

Cho đường tròn (O; 5 cm), điểm M nằm ngoài (O) sao cho hai tiếp tuyến MA và MB (A, B là hai tiếp điểm) vuông góc với nhau tại M.

a) Tính độ dài của MA và MB.

b) Qua giao điểm I của đoạn thẳng MO và đường tròn (O), vẽ một tiếp tuyến cắt OA, OB lần lượt tại C, D. Tính độ dài của CD.

Hướng dẫn giải:

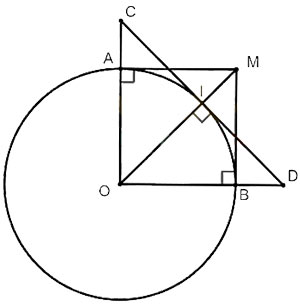
a) Ta có MA và MB là hai tiếp tuyến với (O) tại A và B

nên MA ⊥ OA tại A và MB ⊥ OB tại B

Xét tứ giác OAMB có \(\widehat{OAM}=\widehat{AMB}=\widehat{MBO}=90^{\circ}\)

Suy ra OAMB là hình chữ nhật.

Lại có OA = OB = R

Suy ra OAMB là hình vuông hay MA = MB = R = 5 cm

b) Do MA và MB là hai tiếp tuyến với (O) tại A và B nên OM là tia phân giác của góc \(\widehat{AOB}\)

Xét Δ OCD có OI vừa là đường cao vừa là đường phân giác nên Δ OCD vuông cân tại O.

Mà OI cũng là đường trung tuyến nên CD = 2OI = 2 . 5 = 10 cm

Bài 7

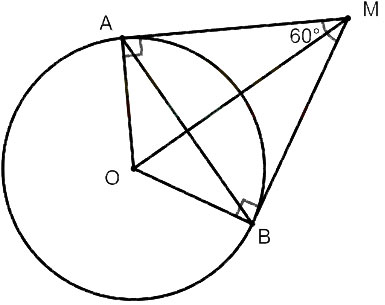
Cho đường tròn (O), điểm M nằm ngoài (O) sao cho MA và MB là hai tiếp tuyến (A, B là hai tiếp điểm) thoả mãn \(\widehat{AMB}=60^{\circ}\). Biết chu vi tam giác MAB là 18 cm, tính độ dài dây AB.

Hướng dẫn giải:

Bài 8

Trong Hình 18, AB là tiếp tuyến của đường tròn (O) tại B.

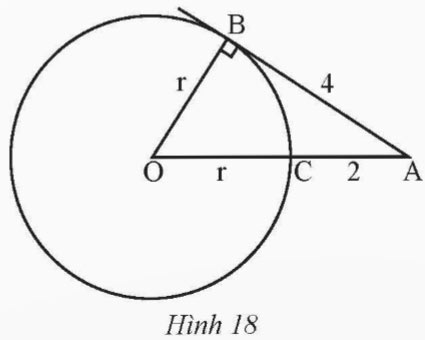
a) Tính bán kính r của đường tròn (O).

b) Tính chiều dài cạnh OA của tam giác ABO.