| |
Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai Giải Toán 9 Chân trời sáng tạo tập 1 trang 52, 53, 54, 55, 56
Bài trước
Giải Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai là tài liệu vô cùng hữu ích giúp các em học sinh lớp 9 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 9 Chân trời sáng tạo tập 1 trang 52, 53, 54, 55, 56.
Giải bài tập Toán 9 Chân trời sáng tạo tập 1 trang 52 → 56 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh ôn tập Bài 4 Chương III: Căn thức - Phần Số và đại số. Mời thầy cô và các em theo dõi bài viết dưới đây của Eballsviet.com:
Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai Chân trời sáng tạo
Giải Toán 9 Chân trời sáng tạo Tập 1 trang 56
Bài 1
Trục căn thức ở mẫu các biểu thức sau:
| a) |
b) |
c) |
Hướng dẫn giải:
a) ![]() \(\frac{2\sqrt{5}}{\sqrt{2}}=\frac{2\sqrt{5}.\sqrt{2}}{\sqrt{2}.\sqrt{2}}=\frac{2\sqrt{10}}{2}=\sqrt{10}\)
\(\frac{2\sqrt{5}}{\sqrt{2}}=\frac{2\sqrt{5}.\sqrt{2}}{\sqrt{2}.\sqrt{2}}=\frac{2\sqrt{10}}{2}=\sqrt{10}\)
b) ![]() \(\frac{10}{3\sqrt{5}}=\frac{10.\sqrt{5}}{3\sqrt{5}.\sqrt{5}}=\frac{10\sqrt{5}}{3.5}=\frac{2\sqrt{5}}{3}\)
\(\frac{10}{3\sqrt{5}}=\frac{10.\sqrt{5}}{3\sqrt{5}.\sqrt{5}}=\frac{10\sqrt{5}}{3.5}=\frac{2\sqrt{5}}{3}\)
c) ![]() \(-\frac{3\sqrt{a}}{\sqrt{12a}}\) với a > 0
\(-\frac{3\sqrt{a}}{\sqrt{12a}}\) với a > 0
 \(=-\frac{3\sqrt{a}.\sqrt{12a}}{\sqrt{12a}.\sqrt{12a}}=-\frac{3\sqrt{\left(2a\right)^2.3}}{\sqrt{\left(12a\right)^2}}\)
\(=-\frac{3\sqrt{a}.\sqrt{12a}}{\sqrt{12a}.\sqrt{12a}}=-\frac{3\sqrt{\left(2a\right)^2.3}}{\sqrt{\left(12a\right)^2}}\)
![]() \(=-\frac{3.\left|2a\right|\sqrt{3}}{\left|12a\right|}=-\frac{3.2a\sqrt{3}}{12a}=-\frac{\sqrt{3}}{2}\)
\(=-\frac{3.\left|2a\right|\sqrt{3}}{\left|12a\right|}=-\frac{3.2a\sqrt{3}}{12a}=-\frac{\sqrt{3}}{2}\)
Bài 2
Khử mẫu của biểu thức lấy căn:
|
a) c) |
b) d) |
Hướng dẫn giải:
a) ![]() \(\sqrt{\frac{4}{7}}=\sqrt{\frac{4.7}{7.7}}=\frac{\sqrt{2^2.7}}{\sqrt{7^2}}=\frac{2\sqrt{7}}{7}\)
\(\sqrt{\frac{4}{7}}=\sqrt{\frac{4.7}{7.7}}=\frac{\sqrt{2^2.7}}{\sqrt{7^2}}=\frac{2\sqrt{7}}{7}\)
b)  \(\sqrt{\frac{5}{24}}=\sqrt{\frac{5.24}{24^2}}=\frac{\sqrt{5.2^2.6}}{\sqrt{24^2}}=\frac{2\sqrt{30}}{24}=\frac{\sqrt{30}}{12}\)
\(\sqrt{\frac{5}{24}}=\sqrt{\frac{5.24}{24^2}}=\frac{\sqrt{5.2^2.6}}{\sqrt{24^2}}=\frac{2\sqrt{30}}{24}=\frac{\sqrt{30}}{12}\)
c) ![]() \(\sqrt{\frac{2}{3a^3}}\) với a > 0
\(\sqrt{\frac{2}{3a^3}}\) với a > 0
 \(=\sqrt{\frac{2.3a^3}{\left(3a^3\right)^2}}=\frac{\sqrt{a^2.6a}}{\sqrt{\left(3a^3\right)^2}}=\frac{\left|a\right|\sqrt{6a}}{\left|3a^3\right|}=\frac{\sqrt{6a}}{3a^2}\) (vì a > 0)
\(=\sqrt{\frac{2.3a^3}{\left(3a^3\right)^2}}=\frac{\sqrt{a^2.6a}}{\sqrt{\left(3a^3\right)^2}}=\frac{\left|a\right|\sqrt{6a}}{\left|3a^3\right|}=\frac{\sqrt{6a}}{3a^2}\) (vì a > 0)
d) ![]() \(2ab\sqrt{\frac{a^2}{2b}}\) với a < 0, b > 0
\(2ab\sqrt{\frac{a^2}{2b}}\) với a < 0, b > 0
 \(=2ab\sqrt{\frac{a^2.2b}{2b.2b}}=2ab\frac{\sqrt{a^2.2b}}{\sqrt{\left(2b\right)^2}}=2ab\frac{\left|a\right|\sqrt{2b}}{\left|2b\right|}\)
\(=2ab\sqrt{\frac{a^2.2b}{2b.2b}}=2ab\frac{\sqrt{a^2.2b}}{\sqrt{\left(2b\right)^2}}=2ab\frac{\left|a\right|\sqrt{2b}}{\left|2b\right|}\)
![]() \(=2ab\frac{\left|a\right|\sqrt{2b}}{\left|2b\right|}=2ab\frac{(-a)\sqrt{2b}}{2b}= -a^2\sqrt{2b}\)
\(=2ab\frac{\left|a\right|\sqrt{2b}}{\left|2b\right|}=2ab\frac{(-a)\sqrt{2b}}{2b}= -a^2\sqrt{2b}\)
Bài 3
Trục căn thức ở mẫu các biểu thức sau:
a) ![]() \(\frac{4}{\sqrt{13}-3}\)
\(\frac{4}{\sqrt{13}-3}\)
b) ![]() \(\frac{10}{5+2\sqrt{5}}\)
\(\frac{10}{5+2\sqrt{5}}\)
c) ![]() \(\frac{\sqrt{a}-\sqrt{b}}{\sqrt{a}+\sqrt{b}}\) với a > 0, b > 0, a ≠ b
\(\frac{\sqrt{a}-\sqrt{b}}{\sqrt{a}+\sqrt{b}}\) với a > 0, b > 0, a ≠ b
Hướng dẫn giải:
a)  \(\frac{4}{\sqrt{13}-3}=\frac{4\left(\sqrt{13}+3\right)}{\left(\sqrt{13}-3\right)\left(\sqrt{13}+3\right)}\)
\(\frac{4}{\sqrt{13}-3}=\frac{4\left(\sqrt{13}+3\right)}{\left(\sqrt{13}-3\right)\left(\sqrt{13}+3\right)}\)
![]() \(=\frac{4\left(\sqrt{13}+3\right)}{13-9}=\sqrt{13}+3\)
\(=\frac{4\left(\sqrt{13}+3\right)}{13-9}=\sqrt{13}+3\)
b)  \(\frac{10}{5+2\sqrt{5}}=\frac{10\left(5-2\sqrt{5}\right)}{\left(5+2\sqrt{5}\right)\left(5-2\sqrt{5}\right)}\)
\(\frac{10}{5+2\sqrt{5}}=\frac{10\left(5-2\sqrt{5}\right)}{\left(5+2\sqrt{5}\right)\left(5-2\sqrt{5}\right)}\)
![]() \(=\frac{10\left(5-2\sqrt{5}\right)}{25-20}\)
\(=\frac{10\left(5-2\sqrt{5}\right)}{25-20}\)
![]() \(=2\left(5-2\sqrt{5}\right)=10-4\sqrt{5}\)
\(=2\left(5-2\sqrt{5}\right)=10-4\sqrt{5}\)
c) ![]() \(\frac{\sqrt{a}-\sqrt{b}}{\sqrt{a}+\sqrt{b}}\) với a > 0, b > 0, a ≠ b
\(\frac{\sqrt{a}-\sqrt{b}}{\sqrt{a}+\sqrt{b}}\) với a > 0, b > 0, a ≠ b
 \(=\frac{\left(\sqrt{a}-\sqrt{b}\right)^2}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}=\frac{a-2\sqrt{ab}+b}{a-b}\)
\(=\frac{\left(\sqrt{a}-\sqrt{b}\right)^2}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}=\frac{a-2\sqrt{ab}+b}{a-b}\)
Bài 4
Rút gọn các biểu thức sau:
a) ![]() \(2\sqrt{3}-\sqrt{27}\)
\(2\sqrt{3}-\sqrt{27}\)
b) ![]() \(\sqrt{45}-\sqrt{20}+\sqrt{5}\)
\(\sqrt{45}-\sqrt{20}+\sqrt{5}\)
c) ![]() \(\sqrt{64a}-\sqrt{18}-a\sqrt{\frac{9}{a}}+\sqrt{50}\) với a > 0
\(\sqrt{64a}-\sqrt{18}-a\sqrt{\frac{9}{a}}+\sqrt{50}\) với a > 0
Hướng dẫn giải:
a) ![]() \(2\sqrt{3}-\sqrt{27} =2\sqrt{3}-\sqrt{3^2.3}\)
\(2\sqrt{3}-\sqrt{27} =2\sqrt{3}-\sqrt{3^2.3}\)
![]() \(=2\sqrt{3}-3\sqrt{ 3} = - \sqrt{ 3}\)
\(=2\sqrt{3}-3\sqrt{ 3} = - \sqrt{ 3}\)
b) ![]() \(\sqrt{45}-\sqrt{20}+\sqrt{5}\)
\(\sqrt{45}-\sqrt{20}+\sqrt{5}\) ![]() \(=\sqrt{3^2.5}-\sqrt{2^2.5}+\sqrt{5}\)
\(=\sqrt{3^2.5}-\sqrt{2^2.5}+\sqrt{5}\)
![]() \(=3\sqrt{ 5}-2\sqrt{ 5}+\sqrt{5}\)
\(=3\sqrt{ 5}-2\sqrt{ 5}+\sqrt{5}\)
![]() \(=2\sqrt{5}\)
\(=2\sqrt{5}\)
c) ![]() \(\sqrt{64a}-\sqrt{18}-a\sqrt{\frac{9}{a}}+\sqrt{50}\) với a > 0
\(\sqrt{64a}-\sqrt{18}-a\sqrt{\frac{9}{a}}+\sqrt{50}\) với a > 0
 \(=\sqrt{8^2.a}-\sqrt{3^2.2}- \sqrt{a^2.\frac{3^2}{a}}+\sqrt{5^2.2}\)
\(=\sqrt{8^2.a}-\sqrt{3^2.2}- \sqrt{a^2.\frac{3^2}{a}}+\sqrt{5^2.2}\)
![]() \(=8\sqrt{ a}-3\sqrt{ 2}-3\sqrt{a}+5\sqrt{ 2}\)
\(=8\sqrt{ a}-3\sqrt{ 2}-3\sqrt{a}+5\sqrt{ 2}\)
![]() \(=5\sqrt{ a}+2\sqrt{ 2}\)
\(=5\sqrt{ a}+2\sqrt{ 2}\)
Bài 5
Tính:
a) ![]() \(\left(\sqrt{\frac{4}{3}}+\sqrt{3}\right)\sqrt{6}\)
\(\left(\sqrt{\frac{4}{3}}+\sqrt{3}\right)\sqrt{6}\)
b) ![]() \(\sqrt{18}:\sqrt{6}+\sqrt{8}.\sqrt{\frac{27}{2}}\)
\(\sqrt{18}:\sqrt{6}+\sqrt{8}.\sqrt{\frac{27}{2}}\)
c) ![]() \(\left(1-2\sqrt{5}\right)^2\)
\(\left(1-2\sqrt{5}\right)^2\)
Bài 6
Chứng minh rằng:
a) ![]() \(\frac{a\sqrt{b}-b\sqrt{a}}{\sqrt{ab}}:\frac{1}{\sqrt{a}+\sqrt{b}}=a-b\) với a > 0, b > 0
\(\frac{a\sqrt{b}-b\sqrt{a}}{\sqrt{ab}}:\frac{1}{\sqrt{a}+\sqrt{b}}=a-b\) với a > 0, b > 0
b) ![]() \(\left(1+\frac{a+\sqrt{a}}{\sqrt{a}+1}\right)\left(1-\frac{a-\sqrt{a}}{\sqrt{a}-1}\right)=1-a\) với a ≥ 0 và a ≠ 1
\(\left(1+\frac{a+\sqrt{a}}{\sqrt{a}+1}\right)\left(1-\frac{a-\sqrt{a}}{\sqrt{a}-1}\right)=1-a\) với a ≥ 0 và a ≠ 1
Bài 7
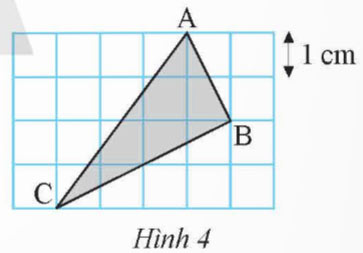
Tam giác ABC được vẽ trên lưới ô vuông như Hình 4. Tính diện tích và chu vi của tam giác ABC.
Bài 8
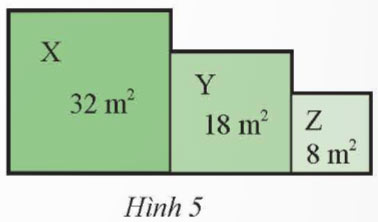
Một vườn hoa gồm ba thửa hình vuông X, Y, Z lần lượt có diện tích như Hình 5. Tính chu vi của vườn hoa đó.
Liên kết tải về
Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai
178,9 KB
Tải về
Xác thực tài khoản!
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
Số điện thoại chưa đúng định dạng!
Sắp xếp theo
Chủ đề liên quan
Tìm bài trong mục này
Đóng
Chỉ thành viên Download Pro tải được nội dung này!
Download Pro - Tải nhanh, website không quảng cáo!
Tìm hiểu thêm













 Đề thi giữa kì 2 lớp 9
Đề thi giữa kì 2 lớp 9
 Đề thi học kì 2 Lớp 9
Đề thi học kì 2 Lớp 9
 Đề thi giữa kì 1 lớp 9
Đề thi giữa kì 1 lớp 9
 Đề thi học kì 1 Lớp 9
Đề thi học kì 1 Lớp 9
 Toán 9
Toán 9
 Toán 9 Kết nối tri thức
Toán 9 Kết nối tri thức
 Toán 9 Cánh Diều
Toán 9 Cánh Diều
 Toán 9 Chân trời sáng tạo
Toán 9 Chân trời sáng tạo
 Văn 9 Kết nối tri thức
Văn 9 Kết nối tri thức









