Toán 8 Bài 4: Tính chất đường phân giác của tam giác Giải Toán 8 Cánh diều tập 2 trang 66, 67, 68, 69
Giải Toán 8 Bài 4: Tính chất đường phân giác của tam giác là tài liệu vô cùng hữu ích giúp các em học sinh lớp 8 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 8 Cánh diều tập 2 trang 66, 67, 68, 69.
Giải bài tập Toán 8 Cánh diều tập 2 trang 66 → 69 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh ôn tập Bài 4 Chương VIII: Tam giác đồng dạng, hình đồng dạng. Vậy mời thầy cô và các em theo dõi bài viết dưới đây của Eballsviet.com:
Toán 8 Bài 4: Tính chất đường phân giác của tam giác Cánh diều
Giải Toán 8 Cánh diều Tập 2 trang 69
Bài 1
Cho tam giác ABC có ba đường phân giác AD, BE, CF. Biết AB = 4, BC = 5, CA = 6. Tính BD, CE, AF.
Lời giải:
AD là đường phân giác của góc BAC nên  \(\frac{BD}{CD}=\frac{AB}{AC}\)
\(\frac{BD}{CD}=\frac{AB}{AC}\)
Mà CD = BC - BD
Suy ra:  \(\frac{BD}{BC-BD}=\frac{AB}{AC}\) hay
\(\frac{BD}{BC-BD}=\frac{AB}{AC}\) hay  \(\frac{BD}{5-BD}=\frac{4}{6}\)
\(\frac{BD}{5-BD}=\frac{4}{6}\)
Do đó: BD = 2.
BE là đường phân giác của góc ABC nên  \(\frac{CE}{AE}=\frac{BC}{AB}\)
\(\frac{CE}{AE}=\frac{BC}{AB}\)
Mà AE = AC - CE
Suy ra:  \(\frac{CE}{AC-CE}=\frac{BC}{AB}\) hay
\(\frac{CE}{AC-CE}=\frac{BC}{AB}\) hay  \(\frac{CE}{6-CE}=\frac{5}{4}\)
\(\frac{CE}{6-CE}=\frac{5}{4}\)
Do đó: CE =  \(\frac{10}{3}\).
\(\frac{10}{3}\).
CF là đường phân giác của góc ACB nên  \(\frac{AF}{BF}=\frac{AC}{BC}\)
\(\frac{AF}{BF}=\frac{AC}{BC}\)
Mà BF = AB - AF
Suy ra:  \(\frac{AF}{AB-AF}=\frac{AC}{BC}\) hay
\(\frac{AF}{AB-AF}=\frac{AC}{BC}\) hay  \(\frac{AF}{4-AF}=\frac{6}{5}\)
\(\frac{AF}{4-AF}=\frac{6}{5}\)
Do đó: AF =  \(\frac{24}{11}\).
\(\frac{24}{11}\).
Bài 2
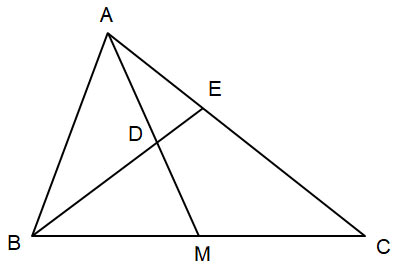
Cho tam giác ABC có đường trung tuyến AM. Tia phân giác của góc ABC lần lượt cắt các đoạn thẳng AM, AC tại điểm D, E. Chứng minh  \(\frac{EC}{EA}=2\frac{DM}{DA}\).
\(\frac{EC}{EA}=2\frac{DM}{DA}\).
Lời giải:
Tam giác ABC có BE là đường phân giác nên  \(\frac{EC}{EA}=\frac{BC}{AB}\)
\(\frac{EC}{EA}=\frac{BC}{AB}\)
Mà M là trung điểm của BC (AM là đường trung tuyến) nên BC = 2BM
Suy ra:  \(\frac{EC}{EA}=2\frac{BM}{AB}\) (1)
\(\frac{EC}{EA}=2\frac{BM}{AB}\) (1)
Tam giác ABM có BD là đường phân giác nên  \(\frac{DM}{DA}=\frac{BM}{AB}\) (2)
\(\frac{DM}{DA}=\frac{BM}{AB}\) (2)
Từ (1)(2) suy ra:  \(\frac{EC}{EA}=2\frac{DM}{DA}\).
\(\frac{EC}{EA}=2\frac{DM}{DA}\).
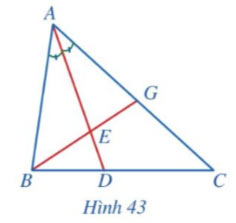
Bài 3
Quan sát Hình 43 và chứng minh  \(\frac{DB}{DC}:\frac{EB}{EG}=\frac{AG}{AC}\).
\(\frac{DB}{DC}:\frac{EB}{EG}=\frac{AG}{AC}\).
Lời giải:
Tam giác ABC có AD là đường phân giác nên  \(\frac{DB}{DC}=\frac{AB}{AC}\)
\(\frac{DB}{DC}=\frac{AB}{AC}\)
Tam giác ABG có AE là đường phân giác nên  \(\frac{EB}{EG}=\frac{AB}{AG}\)
\(\frac{EB}{EG}=\frac{AB}{AG}\)
Do đó:  \(\frac{DB}{DC}:\frac{EB}{EG}=\frac{AB}{AC}:\frac{AB}{AG}=\frac{AB}{AC}.\frac{AG}{AB}=\frac{AG}{AC}\).
\(\frac{DB}{DC}:\frac{EB}{EG}=\frac{AB}{AC}:\frac{AB}{AG}=\frac{AB}{AC}.\frac{AG}{AB}=\frac{AG}{AC}\).
Bài 4
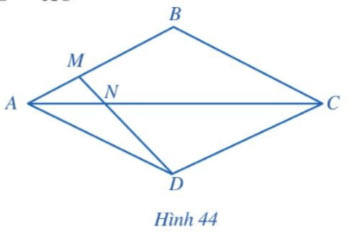
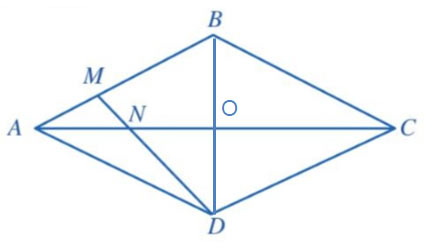
Cho hình thoi ABCD (Hình 44). Điểm M thuộc cạnh AB thỏa mãn AB = 3AM. Hai đoạn thẳng AC và DM cắt nhau tại N. Chứng minh ND = 3MN.
Lời giải:
Gọi giao điểm hai đường chéo AC và BD là O.
Vì ABCD là hình thoi nên AC vuông góc với BD tại O.
Tam giác ABD cân tại A có AO là đường cao nên AO cũng là đường phân giác của góc BAD.
Tam giác AMD có AN là đường phân giác của góc MAD nên  \(\frac{ND}{MN}=\frac{AD}{AM}\) (1)
\(\frac{ND}{MN}=\frac{AD}{AM}\) (1)
Ta có: AM =  \(\frac{1}{3}\)AB mà AD = AB
\(\frac{1}{3}\)AB mà AD = AB
Suy ra: AM =  \(\frac{1}{3}\)AD. (2)
\(\frac{1}{3}\)AD. (2)
Từ (1)(2) suy ra:  \(\frac{ND}{MN}=\frac{AD}{\frac{1}{3}AD}\) hay
\(\frac{ND}{MN}=\frac{AD}{\frac{1}{3}AD}\) hay  \(\frac{ND}{MN}=3\).
\(\frac{ND}{MN}=3\).
Do đó: ND = 3MN.
Bài 5
Cho tam giác ABC vuông tại A có AB = 3, AC = 4, AD là đường phân giác. Tính:
a) Độ dài các đoạn thẳng BC, DB, DC;
b) Khoảng cách từ điểm D đến đường thẳng AC;
c) Độ dài đường phân giác AD.
Lời giải:
a) Tam giác ABC vuông tại A:  \(AB^{2}+AC^{2}=BC^{2}\)
\(AB^{2}+AC^{2}=BC^{2}\)
Suy ra: BC =  \(\sqrt{AB^{2}+AC^{2}}\) = 5
\(\sqrt{AB^{2}+AC^{2}}\) = 5
Do AD là đường phân giác của tam giác ABC nên  \(\frac{DB}{DC}=\frac{AB}{AC}\)
\(\frac{DB}{DC}=\frac{AB}{AC}\)
Mà DC = BC - DB
Nên  \(\frac{DB}{BC-DB}=\frac{AB}{AC}\) hay
\(\frac{DB}{BC-DB}=\frac{AB}{AC}\) hay  \(\frac{DB}{5-DB}=\frac{3}{4}\)
\(\frac{DB}{5-DB}=\frac{3}{4}\)
Do đó: DB =  \(\frac{15}{7}\); DC = 5 -
\(\frac{15}{7}\); DC = 5 -  \(\frac{15}{7}\) =
\(\frac{15}{7}\) =  \(\frac{20}{7}\)
\(\frac{20}{7}\)
b) Từ D kẻ đường thẳng DE vuông góc với AC. DE là khoảng cách từ D đến đường thẳng AC.
Ta có: DE // AB (cùng vuông góc với AC)
Suy ra:  \(\frac{DE}{AB}=\frac{DC}{BC}\) hay
\(\frac{DE}{AB}=\frac{DC}{BC}\) hay  \(\frac{DE}{3}=\frac{\frac{20}{7}}{5}\)
\(\frac{DE}{3}=\frac{\frac{20}{7}}{5}\)
Do đó: DE =  \(\frac{12}{7}\).
\(\frac{12}{7}\).
c) Vì DE // AB nên  \(\frac{BD}{BC}=\frac{AE}{AC}\) hay
\(\frac{BD}{BC}=\frac{AE}{AC}\) hay  \(\frac{\frac{15}{7}}{5}=\frac{AE}{4}\)
\(\frac{\frac{15}{7}}{5}=\frac{AE}{4}\)
Suy ra: AE =  \(\frac{12}{7}\).
\(\frac{12}{7}\).
Tam giác ADE vuông tại E:  \(AD=\sqrt{AE^{2}+DE^{2}}=\frac{12\sqrt{2}}{7}\).
\(AD=\sqrt{AE^{2}+DE^{2}}=\frac{12\sqrt{2}}{7}\).
Bài 6
Cho tứ giác ABCD với các tia phân giác của các góc CAD và CBD cùng đi qua điểm E thuộc cạnh CD (Hình 45). Chứng minh AD.BC = AC.BD.
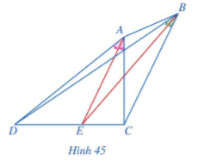
Lời giải:
Tam giác ACD có AE là đường phân giác của góc CAD.
Suy ra:  \(\frac{DE}{EC}=\frac{AD}{AC}\) (1)
\(\frac{DE}{EC}=\frac{AD}{AC}\) (1)
Tam giác BCD có BE là đường phân giác của góc CBD.
Suy ra:  \(\frac{DE}{EC}=\frac{BD}{BC}\) (2)
\(\frac{DE}{EC}=\frac{BD}{BC}\) (2)
Từ (1)(2) suy ra:  \(\frac{AD}{AC}=\frac{BD}{BC}\) hay AD.BC = AC.BD.
\(\frac{AD}{AC}=\frac{BD}{BC}\) hay AD.BC = AC.BD.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:













 Toán 8 Kết nối tri thức
Toán 8 Kết nối tri thức
 Toán 8 Cánh Diều
Toán 8 Cánh Diều
 Toán 8 Chân trời sáng tạo
Toán 8 Chân trời sáng tạo
 Toán 8
Toán 8
 Soạn Văn 8 Kết nối tri thức
Soạn Văn 8 Kết nối tri thức
 Soạn văn 8 Chân trời sáng tạo
Soạn văn 8 Chân trời sáng tạo
 Soạn Văn 8 Cánh Diều
Soạn Văn 8 Cánh Diều
 Chuyên đề Ngữ văn 8
Chuyên đề Ngữ văn 8
 Văn mẫu 8 Kết nối tri thức
Văn mẫu 8 Kết nối tri thức
 Văn mẫu 8 Chân trời sáng tạo
Văn mẫu 8 Chân trời sáng tạo