Toán 8 Bài tập cuối chương V Giải Toán 8 Cánh diều trang 120, 121
Giải Toán 8 Bài tập cuối chương V - Tam giác, tứ giác là tài liệu vô cùng hữu ích giúp các em học sinh lớp 8 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 8 Cánh diều tập 1 trang 120, 121.
Giải bài tập Toán 8 Cánh diều tập 1 trang 120, 121 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh học tập. Vậy mời thầy cô và các em theo dõi bài viết dưới đây của Eballsviet.com:
Toán 8 Bài tập cuối chương V - Tam giác, tứ giác Cánh diều
Giải Toán 8 Cánh diều Tập 1 trang 120, 121
Bài 1
Cho tứ giác ABCD có  \(\widehat{A} = 60^{\circ}, \widehat{B}= 70^{\circ}, \widehat{C} = 80^{\circ}\). Khi đó
\(\widehat{A} = 60^{\circ}, \widehat{B}= 70^{\circ}, \widehat{C} = 80^{\circ}\). Khi đó  \(\widehat{D}\) bằng:
\(\widehat{D}\) bằng:
A.  \(130^{\circ}\)
\(130^{\circ}\)
B.  \(140^{\circ}\)
\(140^{\circ}\)
C.  \(150^{\circ}\)
\(150^{\circ}\)
D.  \(160^{\circ}\)
\(160^{\circ}\)
Lời giải: Chọn C
Bài 2
Cho hình thang cân ABCD có AB//CD,  \(\widehat{A} = 80^{\circ}\). Khi đó
\(\widehat{A} = 80^{\circ}\). Khi đó  \(\widehat{C}\) bằng:
\(\widehat{C}\) bằng:
A.  \(80^{\circ}\)
\(80^{\circ}\)
B.  \(90^{\circ}\)
\(90^{\circ}\)
C.  \(100^{\circ}\)
\(100^{\circ}\)
D.  \(110^{\circ}\)
\(110^{\circ}\)
Lời giải: Chọn C
Bài 3
Cho hình bình hành MNPQ có các góc khác  \(90^{\circ}\), MP cắt NQ tại I. Khi đó
\(90^{\circ}\), MP cắt NQ tại I. Khi đó
A. IM =IN.
B. IM = lP.
C. IM = IQ.
D. IM = MP.
Lời giải: Chọn B
Bài 4
Cho hình chữ nhật MNPQ. Đoạn thắng MP bằng đoạn thẳng nào sau đây?
A. NQ.
B. AN.
C. NP.
D. QM.
Lời giải: Chọn A
Bài 5
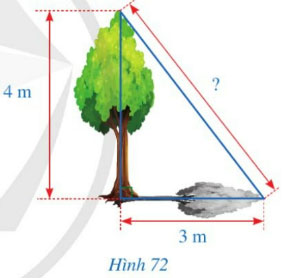
Hình 72 mô tả một cây cao 4 m. Biết rằng khi trời nắng, cây đổ bóng trên mặt đất, điểm xa nhất của bóng cây cách gốc cây một khoảng là 3 m. Tính khoảng cách từ điểm xa nhất của bóng cây đến đỉnh của cây.
Lời giải:
Khoảng cách từ điểm xa nhất của bóng cây đến đỉnh của cây:
 \(\sqrt{3^{2}+4^{2}} = 5\) (m)
\(\sqrt{3^{2}+4^{2}} = 5\) (m)
Bài 6
Màn hình một chiếc ti vi có dạng hình chữ nhật với kích thước màn hình ti vi được tính bằng độ dài đường chéo của màn hình (đơn vị: inch, trong đó 1 inch = 2,54 cm). Người ta đưa ra công thức tính khoảng cách an toàn khi xem ti vi để giúp khách hàng chọn được chiếc ti vi phù hợp với căn phòng của mình như sau:
Khoảng cách tối thiểu = 5,08 . d (cm);
Khoảng cách tối đa = 7,62. d (cm).
Trong đó, ở là kích thước màn hình ti vi tính theo inch.
Với một chiếc vi có chiều dài màn hình là 74,7 cm; chiều rộng màn hình là 32 cm:
a) Kích thước màn hình của chiếc ti vi đó là bao nhiêu inch (làm tròn kết quả đến hàng đơn vị)?
b) Khoảng cách tối thiểu và khoảng cách tối đa để xem chiếc ti ví đó là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
Lời giải:
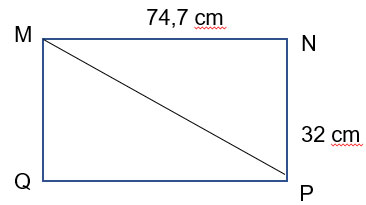
a. Đường chéo màn hình ti vi là:  \(\sqrt{74,7^{2}+32^{2}} \approx\) 81,3 (cm)
\(\sqrt{74,7^{2}+32^{2}} \approx\) 81,3 (cm)
=> Kích thước màn hình của chiếc ti vi đó là: 81,3 : 2,54  \(\approx\) 32 inch
\(\approx\) 32 inch
b. Khoảng cách tối thiểu = 5,08 . 32 = 162,56 (cm);
Khoảng cách tối đa = 7,62. 32 = 243,84 (cm)
Bài 7
Cho tứ giác ABCD có  \(\widehat{DAB}\) =
\(\widehat{DAB}\) =  \(\widehat{BCD}\) ,
\(\widehat{BCD}\) ,  \(\widehat{ABD}\) =
\(\widehat{ABD}\) =  \(\widehat{CDB}\) . Chứng minh ABCD là hình bình hành
\(\widehat{CDB}\) . Chứng minh ABCD là hình bình hành
Lời giải:
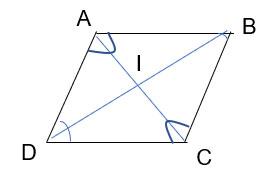
Dựa vào dấu hiệu nhận biết ta có: 2 cặp góc đối  \(\widehat{DAB}\) =
\(\widehat{DAB}\) =  \(\widehat{BCD}\) ,
\(\widehat{BCD}\) ,  \(\widehat{ABD}\) =
\(\widehat{ABD}\) =  \(\widehat{CDB}\) nên ABCD là hình bình hành.
\(\widehat{CDB}\) nên ABCD là hình bình hành.
Bài 8
Cho hình chữ nhật ABCD có M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh tứ giác MNPQ là hình thoi.
Lời giải:
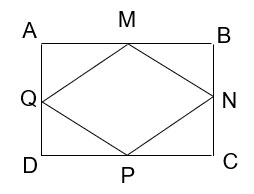
Xét các tam giác vuông:
QAM và NBM có:
- QA = NB
- AM = MB
=> 2 tam giác QAM và NBM bằng nhau (2 cạnh góc vuông) =>MQ=MN (1)
NBM và NCP có:
- NB = NC
- BM = PC
=> 2 tam giác NBM và NCP bằng nhau => NM = NP (2)
NCP và QDP có:
- NC = QD
- CP = DP
=> 2 tam giác NCP và QDP bằng nhau => NP = PQ (3)
Từ (1), (2), (3) => Tứ giác MNPQ có 4 cạnh MQ=MN = NP = PQ nên là hình thoi.
Bài 9
Cho tam giác ABC vuông cân tại C. Trên các cạnh AC, BC lần lượt lấy các điểm D, G sao cho AD = CG < AC. Từ điểm D kẻ DE vuông góc với AC (E thuộc AB). Chứng minh tứ giác CDEG là hình chữ nhật.
Lời giải:
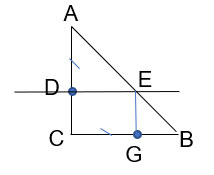
Tam giác ABC vuông cân tại C nên  \(\widehat{A}=\widehat{B}=45^{\circ}\)
\(\widehat{A}=\widehat{B}=45^{\circ}\)
Xét tam giác vuông ADE tại D và có  \(\widehat{A}=45^{\circ}\)=>
\(\widehat{A}=45^{\circ}\)=> \(\widehat{AED}=45^{\circ}\) => Tam giác ADE vuông cân tại D => DA = DE
\(\widehat{AED}=45^{\circ}\) => Tam giác ADE vuông cân tại D => DA = DE
Mà theo giả thiết DA = CG => DE = CG.
Mặt khác DE và CG cùng vuông góc với AC nên chúng song song với nhau.
Vậy DECG là hình bình hành và có 1 goc vuông là  \(\widehat{C}\) nên là hình chữ nhật (đpcm)
\(\widehat{C}\) nên là hình chữ nhật (đpcm)
Bài 10
Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm M, N, P, Q sao cho AM = BN = CP = DQ < AB. Chứng minh tứ giác MNPQ là hình vuông.
Lời giải:
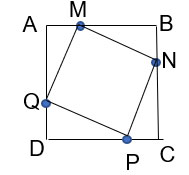
AB = BC, mà AM = BN => AB - AM = BC - BN hay MB = NC. Vậy 2 tam giác vuông MBN = PCN (2 cạnh góc vuông) => MN = NP (1)
BC = DC, mà BN = PC => BC - BN = DC - PC hay NC = DP. Vậy 2 tam giác vuông NCP = PDQ (2 cạnh góc vuông) => NP = PQ (2)
DC = AD, mà PC = QD => DC - PC = AD - QD hay DP = AQ. Vậy 2 tam giác vuông QDP = MAQ (2 cạnh góc vuông) => PQ = MQ (3)
Từ (1), (2), (3) => MNPQ có 4 cạnh bằng nhau nên là hình thoi. (*)
Từ (1) 2 tam giác vuông MBN = PCN =>  \(\widehat{BMN}=\widehat{CNP}\) mà
\(\widehat{BMN}=\widehat{CNP}\) mà  \(\widehat{BMN}+\widehat{BNM} = 90^{\circ}\) =>
\(\widehat{BMN}+\widehat{BNM} = 90^{\circ}\) =>  \(\widehat{CNP}+\widehat{BNM} = 90^{\circ}\) =>
\(\widehat{CNP}+\widehat{BNM} = 90^{\circ}\) =>  \(\widehat{MNP}= 90^{\circ}\) (**)
\(\widehat{MNP}= 90^{\circ}\) (**)
Từ (*) và (**) => Hình thoi MNPQ có 1 góc vuông nên là hình vuông.(đpcm)
Bài 11
Cho hình bình hành ABCD. Gọi M là điểm nằm giữa A và B, N là điểm nằm giữa C và D sao cho AM = CN. Gọi I là giao điểm của MN và AC. Chứng minh:
a)  \(\Delta IAM = \Delta ICN\)
\(\Delta IAM = \Delta ICN\)
b) Tứ giác AMCN là hình bình hành.
c) Ba điểm B, I, D thẳng hàng.
Bài 12
Cho hình thoi ABCD và hình bình hành BCMD. Gọi O là giao điểm của AC và BD.
Chứng minh:
a) OD =  \(\frac{1}{2}\)CM và tam giác ACM là tam giác vuông;
\(\frac{1}{2}\)CM và tam giác ACM là tam giác vuông;
b) Ba điểm A, D, M thẳng hàng;
c) Tam giác DCM là tam giác cân.
Bài 13
Cho hình vuông ABCD có M, N lần lượt là trung điểm của các cạnh BC, CD. Gọi O là giao điểm của AM và BN. Chứng minh:
a)  \(\Delta ABM = \Delta BCN\)
\(\Delta ABM = \Delta BCN\)
b)  \(\widehat{BAO}=\widehat{MBO}\)
\(\widehat{BAO}=\widehat{MBO}\)
c)  \(AM\perp BN\)
\(AM\perp BN\)
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:












 Toán 8 Kết nối tri thức
Toán 8 Kết nối tri thức
 Toán 8 Cánh Diều
Toán 8 Cánh Diều
 Toán 8 Chân trời sáng tạo
Toán 8 Chân trời sáng tạo
 Toán 8
Toán 8
 Soạn Văn 8 Kết nối tri thức
Soạn Văn 8 Kết nối tri thức
 Soạn văn 8 Chân trời sáng tạo
Soạn văn 8 Chân trời sáng tạo
 Soạn Văn 8 Cánh Diều
Soạn Văn 8 Cánh Diều
 Chuyên đề Ngữ văn 8
Chuyên đề Ngữ văn 8
 Văn mẫu 8 Kết nối tri thức
Văn mẫu 8 Kết nối tri thức
 Văn mẫu 8 Chân trời sáng tạo
Văn mẫu 8 Chân trời sáng tạo