Bộ đề thi giữa học kì 1 môn Toán 6 năm 2024 - 2025 sách Cánh diều 5 Đề kiểm tra giữa kì 1 Toán 6 (Có đáp án + Ma trận 3 mức độ)
Bộ đề thi giữa học kì 1 môn Toán 6 Cánh diều năm 2024 - 2025 gồm 5 đề thi, có đáp án, bảng ma trận và đặc tả đề thi giữa kì 1 cho các em ôn tập, nắm chắc cấu trúc đề thi để ôn thi hiệu quả hơn.
Với 5 đề thi giữa kì 1 Toán 6 Cánh diều, còn giúp thầy cô có thêm nhiều kinh nghiệm để xây dựng đề thi giữa học kì 1 năm 2024 - 2025 cho học sinh của mình. Bên cạnh đó, có thể tham khảo thêm đề thi giữa kì 1 môn Khoa học tự nhiên, Tin học, Tiếng Anh 6. Mời thầy cô và các em cùng theo dõi bài viết dưới đây của Eballsviet.com:
Đề thi giữa học kì 1 môn Toán 6 sách Cánh diều
1. Đề thi giữa học kì 1 môn Toán 6 sách Cánh diều - Đề 1
1.1. Đề thi giữa học kì 1 môn Toán 6
|
PHÒNG GD&ĐT .…………… |
ĐỀ KIỂM TRA GIỮA HỌC KÌ I NĂM 2024 - 2025 |
A. PHẦN TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm):
Câu 1: Cho tập hợp M = { 1; 3; 5 }. Kết luận nào sau đây là đúng?
A. 0 ∈ M
B. 1 ∉ M
C. 2 ∈ M
D. 3 ∈ M
Câu 2: Số la Mã XXII biểu diễn số nào trong hệ thập phân?
A. 18
B. 22
C. 202
D. 10102
Câu 3: Chữ số thích hợp ở dấu * để ![]() \(1345<\overline{13 * 5} <1356\)
\(1345<\overline{13 * 5} <1356\)
A. 4
B. 5
C. 6
D. 7
Câu 4: Bác An cần mua một chiếc điện thoại thông minh để cho con học trực tuyến. Giá bán một chiếc điện thoại cùng loại bác An định mua ở bốn cửa hàng như sau:
|
Cửa hàng |
Bình An |
Phú Quý |
Hải Thịnh |
Gia Thành |
|
Giá (đồng) |
6 100 000 |
6 200 000 |
6 150 000 |
5 950 000 |
Bác An nên mua điện thoại ở cửa hàng nào thì có giá rẻ nhất?
A. Gia Thành
B. Phú Quý
C. Hải Thịnh
D. Bình An
Câu 5: Tích 5.5.5.5 viết dưới dạng lũy thừa cơ số 5 là
A. 45
B. 54
C. 525
D. 252
Câu 6: Kết quả của phép tính 46 : 42 được viết dưới dạng lũy thừa là
A. 43
B. 44
C. 48
D. 412
Câu 7: Cho a = 36; b = 3. Khi đó:
A. a ← b
B. b → a
C. a là ước của b
D. a là bội của b
Câu 8: Tập hợp S các số nguyên tố có một chữ số là
A. S = {3; 5; 7; 9}
B. S = {2; 3; 5; 7}
C. S = {3; 5 ; 7}
D. S = {1; 2; 3; 5; 7}
Câu 9: Bức tranh nào dưới đây có dạng hình tam giác đều?

Câu 10: Hình thoi có hai đường chéo là 8cm và 6cm thì diện tích của nó bằng
A. 48cm2
B. 24cm2
C. 28cm2
D. 7cm2
Câu 11: Hình thoi không có đặc điểm nào dưới đây?
A. Bốn cạnh bằng nhau.
B. Bốn góc bằng nhau.
C. Các cạnh đối bằng nhau.
D. Hai đường chéo vuông góc với nhau.
Câu 12: Trong hình bình hành ABCD, cặp cạnh song song là
A. AB và AD
B. BC và AB
C. AD và BC
D. DC và BC

B. PHẦN TỰ LUẬN (7,0 điểm).
Câu 1 (1,0 điểm): Viết tập hợp A các số tự nhiên x biết rằng 10 < x 15.
Câu 2 (1,0 điểm): Không thực hiện phép tính, hãy cho biết tổng 540 + 345 có chia hết cho cả 3 và 5 không? Vì sao?
Câu 3: (1,0 điểm): Tìm x, biết 2021 – x = 715 : 713
Câu 4 (1,0 điểm): Tính giá trị biểu thức: 5 . 42 – 18 : (15 – 12)2
Câu 5 (1,0 điểm): Cô giáo có 5 hộp bút, mỗi hộp bút có 12 chiếc. Hỏi cô giáo có thể chia đều số bút nói trên cho 6 tổ được không? Vì sao?
Câu 6 (0,5 điểm): Dùng thước và compa, vẽ tam giác đều ABC có cạnh bằng 3cm.
Câu 7 (1,0 điểm): Một mảnh đất có dạng hình chữ nhật ABCD, với chiều dài AB = 50m, chiều rộng AD = 30m.
a) Tính diện tích mảnh đất hình chữ nhật AD nói trên.
b) Một dự án mở đường, con đường cắt ngang qua mảnh đất tạo thành hình bình hành AEFH như hình vẽ. Tính phần diện tích còn lại của mảnh đất?

Câu 8 (0,5 điểm): Cho 2021 số tự nhiên, trong đó tổng của năm số bất kì đều là số lẻ. Hỏi tổng của 2021 số tự nhiên đó là số chẵn hay số lẻ?
1.2. Ma trận đề thi giữa học kì 1 môn Toán 6
|
TT |
Chủ đề |
Nội dung/Đơn vị kiến thức |
Mức độ đánh giá |
Tổng % điểm |
||||||||
|
Nhận biết |
Thông hiểu |
Vận dụng |
Vận dụng cao |
|||||||||
|
TNKQ |
TL |
TNKQ |
TL |
TNKQ |
TL |
TNKQ |
TL |
|||||
|
1 |
Số tự nhiên. |
Tập hợp – Tập hợp số tự nhiên. |
Nhận biết phần tử thuộc hay không thuộc tập hợp. |
1 (TN1) |
|
|
1 (TL1) |
|
|
|
2 |
12,5 |
|
Biểu diễn số la Mã trong hệ thập phân. |
1 (TN 2) |
|
|
|
|
|
|
|
2,5 |
|||
|
So sánh số tự nhiên. |
|
|
2 (TN 3, TN 4) |
|
|
|
|
|
5 |
|||
|
Các phép tính với số tự nhiên. Phép tính luỹ thừa với số mũ tự nhiên |
Lũy thừa. |
2 (TN 5, TN6) |
|
|
|
|
1 (TL3) |
|
|
15 |
||
|
Các phép tính. |
|
|
|
|
|
1 (TL4) |
|
1 (TL8) |
15 |
|||
|
Quan hệ chia hết – Số nguyên tố |
Khái niệm về ước và bội, quan hệ chia hết. |
1 (TN 7) |
|
|
1 (TL2) |
|
1 (TL5) |
|
|
22,5 |
||
|
Số nguyên tố. |
1 (TN8) |
|
|
|
|
|
|
|
25 |
|||
|
2 |
Hình học trực quan. |
Hình học trực quan. |
Tam giác đều, hình chữ nhật, hình thoi, hình bình hành. |
4 (TN9, TN11, TN12) |
|
1 (TN10) |
1 (TL7a) |
|
1 (TL6) |
|
1 (TL7B) |
25 |
|
Tổng |
9 |
|
3 |
3 |
|
4 |
|
2 |
|
|||
|
Tỉ lệ % |
22,5 |
|
7,5 |
25 |
|
35 |
|
10 |
100 |
|||
|
Tỉ lệ chung |
55% |
45% |
100 |
|||||||||
1.3. Bản đặc tả đề thi giữa kì 1 môn Toán 6
|
TT |
Chủ đề |
Mức độ đánh giá |
Số câu hỏi theo mức độ nhận thức |
||||
|
Nhận biết |
Thông hiểu |
Vận dụng |
Vận dụng cao |
||||
|
SỐ VÀ ĐẠI SỐ |
|
|
|
|
|||
|
1 |
Số tự nhiên |
Tập hợp – Tập hợp số tự nhiên. |
Nhận biết: – Nhận biết phần tử thuộc hay không thuộc tập hợp. - Biết biểu diễn được số la Mã trong hệ thập phân. - Biết so sánh số tự nhiên. Thông hiểu: - Liệt kê các phần tử của một tập hợp từ điều kiện cho trước. |
4 (TN1, TN2) |
3 (TL1, TN3, TN4) |
|
|
|
Các phép tính với số tự nhiên. Phép tính luỹ thừa với số mũ tự nhiên. |
Nhận biết: – Định nghĩa lũy thừa. Vận dụng: – Thực hiện được các phép tính: cộng, trừ, nhân, chia trong tập hợp số tự nhiên. – Thực hiện được phép tính luỹ thừa với số mũ tự nhiên; thực hiện được các phép nhân và phép chia hai luỹ thừa cùng cơ số với số mũ tự nhiên. |
2 (TN5, TN6) |
|
2 (TL3, TL4) |
1 (TL8) |
||
|
Tính chia hết trong tập hợp các số tự nhiên. Số nguyên tố. Ước chung và bội chung. |
Nhận biết: – Nhận biết được quan hệ chia hết, khái niệm ước và bội. – Nhận biết được khái niệm số nguyên tố, hợp số. Thông hiểu: - Các dấu hiệu chia hết cho 2, 3, 5, 9. Vận dụng: – Vận dụng được dấu hiệu chia hết cho 2, 5, 9, 3 để giải quyết bài toán có nội dung thực tế đơn giản, quen thuộc. |
2 (TN7, TN8) |
1 (TL2) |
1 (TL5) |
|
||
|
HÌNH HỌC TRỰC QUAN |
|
|
|
|
|||
|
2 |
Hình học trực quan |
- Tam giác đều, hình vuông, lục giác đều. - Hình chữ nhật, hình thoi, hình bình hành. |
Nhận biết: – Nhận dạng được tam giác đều, hình vuông, hình chữ nhật, hình thoi, lục giác đều. – Nắm được đặc điểm các hình. Thông hiểu: – Tính được diện tích một số hình . Vận dụng: – Vẽ được một số hình bằng thước và compa. – Biết vận dụng công thức tính diện tích một số hình để giải quyết bài toán thực tế. |
4 (TN9, TN11, TN12) |
2 (TL7a, TN10) |
1 (TL6) |
1 (TL7b) |
2. Đề thi giữa học kì 1 môn Toán 6 sách Cánh diều - Đề 2
2.1. Đề thi giữa học kì 1 môn Toán 6
I. Phần trắc nghiệm (4 điểm)
Câu 1: Tập hợp nào dưới đây có 5 phần tử?
A = {x ∈ N ∗ ∈N∗ | x > 3}
B = {x ∈ N ∈N | x < 6}
C = {x ∈ N ∈N | x ≤ 4}
D = {x ∈ N ∗ ∈N∗ | 4 < x ≤ 8}
Câu 2: Cho tập hợp M các số tự nhiên lớn hơn 14, nhỏ hơn 45 và có chứa chữ số 3. Phần tử nào dưới đây không thuộc tập hợp M?
A. 13
B. 23
C. 33
D. 43
Câu 3: Số 1 080 chia hết cho bao nhiêu số trong các số sau đây: 2, 3, 4, 5, 6, 8, 9, 12, 24, 25?
A. 10 số
B. 9 số
C. 8 số
D. 7 số
Câu 4: Hằng gấp được 97 ngôi sao và xếp vào các hộp, mỗi hộp 8 ngôi sao. Số ngôi sao còn thừa không xếp vào hộp là:
A. 5 ngôi sao
B. 1 ngôi sao
C. 6 ngôi sao
D. 2 ngôi sao
Câu 5: Phân tích số 154 ra thừa số nguyên tố được:
A. 154 = 2 . 7 . 11
B. 54 = 1 . 5 . 4
C. 154 = 22 . 3 . 5
D. 154 = 2 . 7 . 13
Câu 6: Hình nào dưới đây là hình vẽ chỉ tam giác đều?
A. 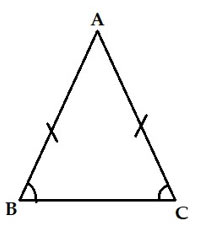
B. 
C. 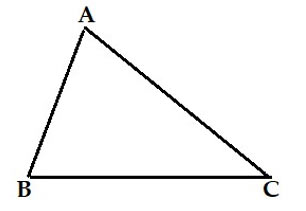
D. 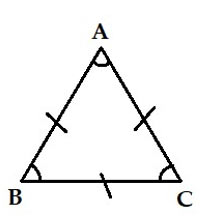
Câu 7: Hai đường chéo hình thoi có độ dài lần lượt bằng 16 cm và 12 cm. Diện tích của hình thoi là:
A. 90 cm2
B. 96 cm2
C. 108 cm2
D.120 cm2
Câu 8: Chọn câu sai trong các câu dưới đây?
Cho hình vẽ
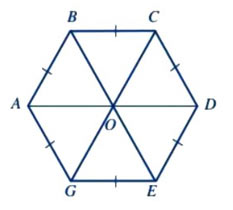
Lục giác đều ABCDEG là hình có:
A. Các góc ở các đỉnh A, B, C, D, E, G, O bằng nhau.
B. Sáu cạnh bằng nhau: AB = BC = CD = DE = EG = GA.
C. Ba đường chéo chính cắt nhau tại điểm O.
D. Ba đường chéo chính bằng nhau: AD = BE = CG.
II. Phần tự luận (6 điểm)
Bài 1 (2 điểm):
1) Thực hiện các phép tính:
a) 30 . 75 + 25 . 30 – 150;
b) 160 – (4 . 52– 3 . 23);
c) [36 . 4 – 4 . (82 – 7 . 11)2] : 4 – 20220.
2) Tìm BCNN của các số 28, 54.
Bài 2 (1,5 điểm): Tính diện tích của hình H gồm hình bình hành ABCD và hình chữ nhật DCNM, biết hình chữ nhật DCNM có chu vi bằng 180 cm và chiều dài MN gấp 4 lần chiều rộng CN.
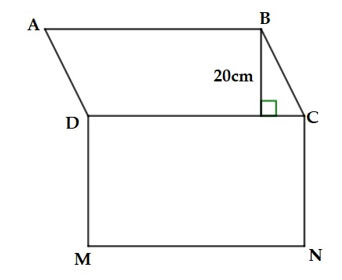
Bài 3 (2 điểm): Một đội y tế gồm 48 bác sĩ và 108 y tá. Hỏi có thể chia đội y tế thành nhiều nhất bao nhiêu tổ để số bác sĩ và y tá được chia đều vào các tổ?
Bài 4 (0,5 điểm): Chứng tỏ A chia hết cho 6 với A = 2 + 22 + 23 + 24 + … + 2100.
2.2. Đáp án đề thi giữa học kì 1 môn Toán 6
I. Phần trắc nghiệm
Bảng đáp án (0,5 × 8 = 4 điểm)
|
Câu 1: C |
Câu 2: A |
Câu 3: B |
Câu 4: B |
|
Câu 5: A |
Câu 6: D |
Câu 7: B |
Câu 8: A |
Hướng dẫn chi tiết
Câu 1:
Viết các tập hợp đã cho dưới dạng liệt kê các phần tử ta được
A = {4; 5; 6; … } (tập hợp A các số tự nhiên lớn hơn 3)
B = {0; 1; 2; 3; 4; 5} (tập hợp B các số tự nhiên nhỏ hơn 6)
C = {0; 1; 2; 3; 4} (tập hợp C các số tự nhiên nhỏ hơn hoặc bằng 4)
D = {5; 6; 7; 8} (tập hợp D các số tự nhiên lớn hơn 4 và nhỏ hơn hoặc bằng 8)
Vậy ta thấy tập hợp C có 5 phần tử.
Chọn đáp án C.
Câu 2:
Tập hợp M gồm các số tự nhiên lớn hơn 14, nhỏ hơn 45 và có chứa chữ số 3.
Ta thấy các số 13, 23, 33, 43 đều có chứa chữ số 3, nhưng 13 < 14 nên 13 không thuộc tập hợp M.
Chọn đáp án A.
Câu 3:
Số 1 080 có chữ số tận cùng là 0 nên nó chia hết cho cả 2 và 5.
Số 1 080 có tổng các chữ số là 1 + 0 + 8 + 0 = 9 chia hết cho 3 và 9 nên nó chia hết cho cả 3 và 9.
Ngoài ra: 1 080 : 4 = 270; 1 080 : 6 = 180; 1 080 : 8 = 135; 1 080 : 12 = 90; 1 080 : 24 = 45; 1 080 : 25 = 43 (dư 5).
Vậy số 1 080 chia hết cho các số: 2, 3, 4, 5, 6, 8, 9, 12, 24.
Do đó nó chia hết cho 9 số trong các số đã cho.
Chọn đáp án B.
Câu 4:
Mỗi hộp có 8 ngôi sao nên ta thực hiện phép chia:
97 : 8 = 12 (dư 1)
Vậy còn thừa 1 ngôi sao không xếp vào hộp.
Chọn đáp án B.
Câu 5:
Ta phân tích 154 ra thừa số nguyên tố:
Vậy 154 = 2 . 7 . 11.
Chọn đáp án A.
Câu 6:
Tam giác đều là hình tam giác có 3 cạnh bằng nhau và 3 góc bằng nhau, vậy trong các hình đã cho, hình vẽ D chỉ tam giác đều.
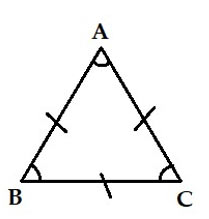
Chọn đáp án D.
Câu 7:
Diện tích hình thoi bằng 1 2 12 tích độ dài hai đường chéo.
Vậy diện tích của hình thoi có độ dài hai đường chéo lần lượt là 16 cm và 12 cm là:
S = 1 2 .16 .12 = 96 S=12.16.12=96 (cm2).
Chọn đáp án B.
Câu 8:
Lục giác đều ABCDEG có các tính chất:
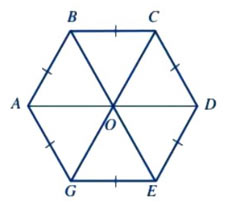
+ Các góc ở các đỉnh A, B, C, D, E, G bằng nhau.
+ Sáu cạnh bằng nhau: AB = BC = CD = DE = EG = GA.
+ Ba đường chéo chính AD, BE, CG cắt nhau tại điểm O.
+ Ba đường chéo chính bằng nhau: AD = BE = CG.
Vậy đáp án A sai (vì góc ở đỉnh O không bằng các góc ở đỉnh của lục giác).
Chọn đáp án A.
II. Phần tự luận
Bài 1:
1) a) 30 . 75 + 25 . 30 – 150
= 30 . (75 + 25) – 150
= 30 . 100 – 150
= 3 000 – 150 = 2 850
b) 160 – (4 . 52– 3 . 23)
= 160 – (4 . 25 – 3 . 8)
= 160 – (100 – 24)
= 160 – 76 = 84
c) [36 . 4 – 4 . (82 – 7 . 11)2] : 4 – 20220
= [36 . 4 – 4 . (82 – 77)2] : 4 – 1
= [36 . 4 – 4 . 52] : 4 – 1
= [36 . 4 – 4 . 25] : 4 – 1
= [4 . (36 – 25)] : 4 – 1
= 4 . 11 : 4 – 1 = 11 – 1 = 10
2) Đề tìm BCNN của 28 và 54, ta phân tích các số đó ra thừa số nguyên tố.
Ta có: 28 = 4 . 7 = 22 . 7
54 = 6 . 9 = 2 . 3 . 32 = 2 . 33
Vậy BCNN(28, 54) = 22 . 33 . 7 = 4 . 27 . 7 = 756.
Bài 2:
Nửa chu vi hình chữ nhật DCNM là: 180 : 2 = 90 (cm)
Khi đó: MN + CN = 90 (cm)
Chiều dài MN gấp 4 lần chiều rộng CN
Tổng số phần bằng nhau là: 1 + 4 = 5 (phần)
Chiều dài MN (hay CD) của hình chữ nhật DCNM là: 90 : 5 . 4 = 72 (cm)
Chiều rộng CN (hay DM) của hình chữ nhật DCNM là: 90 – 72 = 18 (cm)
Diện tích hình chữ nhật DCMN là: 18 . 72 = 1 296 (cm2)
Diện tích hình bình hành ABCD là: 72 . 20 = 1 440 (cm2)
Diện tích hình H là: 1 296 + 1 440 = 2 736 (cm2).
Bài 3:
Gọi x là số tổ nhiều nhất được chia (x là số tự nhiên khác 0).
Vì số bác sĩ được chia đều vào mỗi tổ nên 48 ⁝ x
Số y tá được chia đều vào mỗi tổ nên 108 ⁝ x
Do đó x là ước chung của 48 và 108, mà x là nhiều nhất nên x là ƯCLN của 48 và 108.
Ta có: 48 = 24 . 3
108 = 22 . 33
Suy ra ƯCLN(48, 108) = 22 . 3 = 12 hay x = 12 (thỏa mãn).
Vậy có thể chia được nhiều nhất 12 tổ.
Bài 4:
A = 2 + 22 + 23 + 24 + … + 2100
A = (2 + 22) + (23 + 24) + … + (299 + 2100)
A = 6 + 22 . (2 + 22) + … + 298 . (2 + 22)
A = 6 + 22 . 6 + … + 298 . 6
A = 6 . (1 + 22 + … + 298)
Vậy A chia hết cho 6 (theo tính chất chia hết của một tích).
2.3. Ma trận đề thi giữa học kì 1 môn Toán 6
| Cấp độ Chủ đề | Mức 1 (Nhận biết) |
Mức 2 Thông hiểu |
Mức 3 Vận dụng |
Cộng | |||||
| Cấp độ thấp | Cấp độ cao | ||||||||
| KQ | TL | KQ | TL | KQ | TL | KQ | TL | ||
|
1. Tập hợp các số tự nhiên. |
C1,4: Biết khái niệm về tập hợp, phần tử của tập hợp. C2,3: Chỉ ra cặp số tự nhiên liền trước và liền sau, giá trị của chữ số trong một số tự nhiên |
C(9,10,11): Cộng, trừ, nhân, chia số tự nhiên. C21a,b: Thực hiện được cộng trừ nhân chia STN |
C21c: Vận dụng linh hoạt các phép tính trong N. |
|
|
||||
|
Số câu Số điểm Tỉ lệ % |
4 (C1, 2, 3, 4) 1 10% |
|
3 (C9, 10, 11) 0,75 7,5% |
2/3 C21
1 10% |
|
1/3 C21
1 10% |
|
|
8
3,75 37,5% |
|
Thành tố NL |
C1, 2, 3, 4 - TD
|
|
C9, 10, 11 - GQVĐ |
GQVĐ |
|
GQVĐ |
|
|
|
|
2. Tính chất chia hết trong tập hợp số tự nhiên |
C5,6: Biết được t/c chia hết của 1 tổng C7: Biết được thế nào là số nguyên tố. C8: Biết khái niệm ƯCLN |
C12. Hiểu cách phân tích một số ra thừa số nguyên tố C13. Hiểu t/c chia hết của 1 tổng C14. Hiểu quy tắc tìm BCNN |
C22: Áp dụng quy tắc tìm ƯCLN vào giải bài toán thực tế. |
|
|
||||
|
Số câu Số điểm Tỉ lệ % |
4(5, 6, 7, 8) 1 10% |
|
3 (12, 13, 14) 0,75 7,5% |
|
|
1 (C22)
1,5 15% |
|
1(C24)
0,5 5% |
9
3,75 37,5% |
|
Thành tố NL |
TD |
|
C12,13:GQVĐ C14 TD |
|
|
TD-GQVĐ |
|
TD-GQVĐ |
|
|
3. Một số hình phẳng trong thực tiễn.
|
C15. Biết được số đo góc trong tam giác cân. C16. Nhận biết được yếu tố trong hình vuông. C17,18: Biết công thức tính chu vi hình chữ nhật. Diện tích hình bình hành |
C19,20: Nắm được công thức tính diện tích hình thang và chu vi hình bình hành C23: Áp dụng công thức tính diện tích và chu vi hình chữ nhật để giải bài toán thực tế. |
|
|
|
||||
|
Số câu Số điểm Tỉ lệ % |
4 (15,16, 17, 18) 1 10% |
|
2(C19, 20) 0,5 5% |
1(C23)
1 10% |
|
|
|
|
7
2,5 25% |
|
Thành tố NL |
C15, 16: TD C17, 18: TD, MHH |
|
C19: GQVĐ C20: MHH-GQVĐ
|
MHH-GQVĐ |
|
|
|
|
|
|
Tổng số câu Tổng số điểm Tỉ lệ % |
12
3 30% |
|
9 + 2/3
4 40% |
1+1/3
2,5 25% |
1
0,5 5% |
24
10 100% |
|||
....
>> Tải file để tham khảo trọn bộ đề thi giữa học kì 1 môn Toán 6 năm 2024 - 2025 sách Cánh diều
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:












 Toán 6 Kết nối tri thức
Toán 6 Kết nối tri thức
 Toán 6 Chân trời sáng tạo
Toán 6 Chân trời sáng tạo
 Toán 6 Cánh Diều
Toán 6 Cánh Diều
 Soạn văn 6 Chân trời sáng tạo
Soạn văn 6 Chân trời sáng tạo
 Soạn văn 6 Cánh Diều
Soạn văn 6 Cánh Diều
 Soạn Văn 6 Kết nối tri thức
Soạn Văn 6 Kết nối tri thức
 Tiếng Anh 6 Global Success
Tiếng Anh 6 Global Success
 Tiếng Anh 6 Friends Plus
Tiếng Anh 6 Friends Plus
 Tiếng Anh 6 Explore English
Tiếng Anh 6 Explore English
 Khoa học tự nhiên 6 CTST
Khoa học tự nhiên 6 CTST









