Vật lí 10 Bài 8: Chuyển động biến đổi - Gia tốc Soạn Lý 10 trang 37 sách Kết nối tri thức

Bài trước

Mục lục

Bài sau

Giải Vật lí 10 Bài 8: Chuyển động biến đổi - Gia tốc sách Kết nối tri thức với cuộc sống giúp các em học sinh lớp 10 có thêm nhiều gợi ý tham khảo để biết cách trả lời các câu hỏi bài học Bài 8 trang 37, 38, 39 thuộc chương 2: Động học.

Giải bài tập Vật lý 10 Bài 8: Chuyển động biến đổi - Gia tốc giúp các em hiểu được kiến thức về chuyển động biến đổi, cách tính gia tốc của chuyển động biến đổi, từ đó sẽ biết cách trả lời toàn bộ các câu hỏi của Bài 8 chương II trong sách giáo khoa Vật lí 10 Kết nối tri thức với cuộc sống. Vậy sau đây là nội dung chi tiết bài Soạn Vật lí 10 Bài 8: Chuyển động biến đổi - Gia tốc, mời các bạn cùng tải tại đây.

Giải Vật lí 10 Bài 8: Chuyển động biến đổi - Gia tốc

I. Chuyển động biến đổi

Câu hỏi trang 37

Hãy tìm thêm ví dụ về chuyển động biến đổi trong cuộc sống.

Gợi ý đáp án

- Chuyển động của xe đạp khi xuống dốc.

- Chuyển động của tàu khi sắp cập bến.

- Chuyển động của vận động viên điền kinh khi bắt đầu xuất phát.

II. Gia tốc của chuyển động biến đổi

Câu hỏi 1 trang 38

Xác định độ biến thiên vận tốc sau 8 s của chuyển động trên.

Gợi ý đáp án

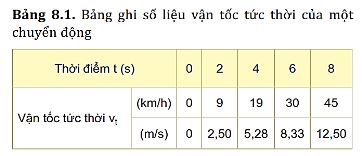
Độ biến thiên vận tốc sau 8 s của chuyển động trên là:

∆v = v₈ - v₀ = 12,5 - 0 = 12,5m/s

Câu hỏi 2 trang 38

Xác định độ biến thiên của vận tốc sau mỗi giây của chuyển động trên trong 4 s đầu và trong 4 s cuối.

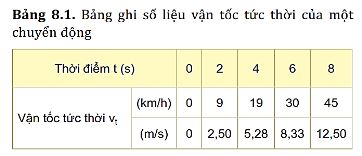
- Độ biến thiên của vận tốc sau mỗi giây của chuyển động trên trong 4 s đầu là:

$\frac{\triangle v}{\triangle t}\;=\;\frac{v_4\;-\;v_0}4\;=\;\frac{5,28\;-\;0}4\;=\;1,32\;m/s^2$ $\frac{\triangle v}{\triangle t}\;=\;\frac{v_4\;-\;v_0}4\;=\;\frac{5,28\;-\;0}4\;=\;1,32\;m/s^2$

- Độ biến thiên của vận tốc sau mỗi giây của chuyển động trên trong 4 s cuối là:

$\frac{\triangle v}{\triangle t}\;=\;\frac{v_8\;-\;v_4}4\;=\;\frac{12,5\;-\;5,28}4\;=\;1,825\;m/s^2$ $\frac{\triangle v}{\triangle t}\;=\;\frac{v_8\;-\;v_4}4\;=\;\frac{12,5\;-\;5,28}4\;=\;1,825\;m/s^2$

Câu hỏi 3 trang 38

Các đại lượng xác định được ở câu 2 cho ta biết điều gì về sự thay đổi vận tốc của chuyển động trên?

Gợi ý đáp án

Các đại lượng xác định được ở câu 2 cho ta biết sự thay đổi nhanh hay chậm của vận tốc.

Câu hỏi 4 trang 38

Hãy chứng tỏ khi $\overrightarrow a$ $\overrightarrow a$ cùng chiều với $\overrightarrow v$ $\overrightarrow v$ (a.v > 0) thì chuyển động là nhanh dần, khi $\overrightarrow a$ $\overrightarrow a$ ngược chiều với $\overrightarrow v$ $\overrightarrow v$ (a.v < 0) thì chuyển động là chậm dần.

Gợi ý đáp án

Ta có biểu thức tính gia tốc: $a\;=\;\frac{\triangle v}{\triangle t}\;=\;\frac{v_t\;-\;v_0}{t\;-\;t_0}$ $a\;=\;\frac{\triangle v}{\triangle t}\;=\;\frac{v_t\;-\;v_0}{t\;-\;t_0}$

- Chọn chiều dương là chiều chuyển động của vật.

- Giả sử vật chuyển động theo chiều dương nên v > 0

thức tính gia tốc thì ∆v > 0 => a > 0

=> a.v > 0

- Khi vật chuyển động chậm dần thì vận tốc giảm dần nên ∆v < 0 => a < 0

=> a.v < 0

Câu hỏi 1 trang 39

a) Tính gia tốc của ô tô trên 4 đoạn đường trong Hình 8.1.

b) Gia tốc của ô tô trên đoạn đường 4 có gì đặc biệt so với sự thay đổi vận tốc trên các đoạn đường khác nhau?

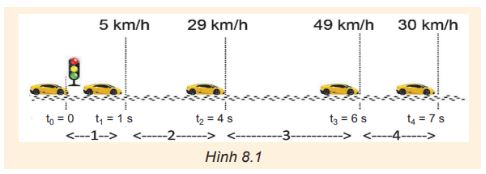
Gợi ý đáp án

a) Đổi 5 km/h 1,39 m/s; 29 km/h 8,06 m/s;

49 km/h 13,61 m/s; 30 km/h 8,33 m/s

- Gia tốc của ô tô trên đoạn đường 1 là: $a_1\;=\;\frac{\triangle v_1}{\triangle t_1}\;=\;\frac{1,39\;-\;0}{1\;-\;0}\;=\;1,39\;m/s^2$ $a_1\;=\;\frac{\triangle v_1}{\triangle t_1}\;=\;\frac{1,39\;-\;0}{1\;-\;0}\;=\;1,39\;m/s^2$

- Gia tốc của ô tô trên đoạn đường 2 là: $a_2\;=\;\frac{\triangle v_2}{\triangle t_2}\;=\;\frac{8,06\;-\;1,39}{4\;-\;1}\;\approx\;2,22\;m/s^2$ $a_2\;=\;\frac{\triangle v_2}{\triangle t_2}\;=\;\frac{8,06\;-\;1,39}{4\;-\;1}\;\approx\;2,22\;m/s^2$

- Gia tốc của ô tô trên đoạn đường 3 là: $a_3\;=\;\frac{\triangle v_3}{\triangle t_3}\;=\;\frac{13,61\;-\;8,06}{6\;-\;4}\;\approx\;2,78\;m/s^2$ $a_3\;=\;\frac{\triangle v_3}{\triangle t_3}\;=\;\frac{13,61\;-\;8,06}{6\;-\;4}\;\approx\;2,78\;m/s^2$

- Gia tốc của ô tô trên đoạn đường 4 là: $a_4\;=\;\frac{\triangle v_4}{\triangle t_4}\;=\;\frac{8,33\;-\;13,61}{7\;-\;6}\;=\;-5,28\;m/s^2$ $a_4\;=\;\frac{\triangle v_4}{\triangle t_4}\;=\;\frac{8,33\;-\;13,61}{7\;-\;6}\;=\;-5,28\;m/s^2$

b) Trên đoạn đường 1, 2, 3 thì gia tốc của xe dương vì vận tốc luôn tăng dần.

Trên đoạn đường 4 thì gia tốc âm vì vận tốc giảm dần.

Câu hỏi 2 trang 39

Một con báo đang chạy với vận tốc 30 m/s thì chuyển động chậm dần khi tới gần một con suối. Trong 3 giây, vận tốc của nó giảm còn 9 m/s. Tính gia tốc của con báo.

Gợi ý đáp án

Gia tốc của con báo là: $a\;=\;\frac{\triangle v}{\triangle t}\;=\;\frac{9\;-\;30}3\;=\;-7\;m/s^2$ $a\;=\;\frac{\triangle v}{\triangle t}\;=\;\frac{9\;-\;30}3\;=\;-7\;m/s^2$

Câu hỏi 3 trang 39

Đồ thị ở Hình 8.2 mô tả sự thay đổi vận tốc theo thời gian trong chuyển động của một ô tô thể thao đang chạy thử về phía Bắc.

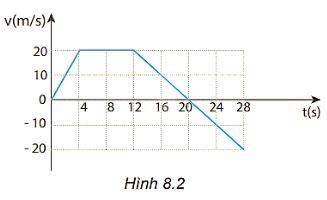
Tính gia tốc của ô tô:

a) Trong 4 s đầu.

b) Từ giây thứ 4 đến giây thứ 12.

c) Từ giây thứ 12 đến giây thứ 20.

d) Từ giây thứ 20 đến giây thứ 28.

Gợi ý đáp án

a) Gia tốc của ô tô trong 4 giây đầu là: $a_1\;=\;\frac{\triangle v_1}{\triangle t_1}\;=\;\frac{20\;-\;0}{4\;-\;0}\;=\;5\;m/s^2$ $a_1\;=\;\frac{\triangle v_1}{\triangle t_1}\;=\;\frac{20\;-\;0}{4\;-\;0}\;=\;5\;m/s^2$

b) Gia tốc của ô tô từ giây thứ 4 đến giây thứ 12 là: $a_2\;=\;\frac{\triangle v_2}{\triangle t_2}\;=\;\frac{20\;-\;20}{12\;-\;4}\;=\;0\;m/s^2$ $a_2\;=\;\frac{\triangle v_2}{\triangle t_2}\;=\;\frac{20\;-\;20}{12\;-\;4}\;=\;0\;m/s^2$

c) Gia tốc của ô tô từ giây thứ 12 đến giây thứ 20 là: $a_3\;=\;\frac{\triangle v_3}{\triangle t_3}\;=\;\frac{0\;-\;20}{20\;-\;12}\;=\;-2,5\;m/s^2$ $a_3\;=\;\frac{\triangle v_3}{\triangle t_3}\;=\;\frac{0\;-\;20}{20\;-\;12}\;=\;-2,5\;m/s^2$

d) Gia tốc của ô tô từ giây thứ 20 đến giây thứ 28 là: $a_4\;=\;\frac{\triangle v_4}{\triangle t_4}\;=\;\frac{-20\;-\;0}{28\;-\;20}\;=\;-2,5\;m/s^2$ $a_4\;=\;\frac{\triangle v_4}{\triangle t_4}\;=\;\frac{-20\;-\;0}{28\;-\;20}\;=\;-2,5\;m/s^2$

Chia sẻ bởi: