Vật lí 10 Bài 9: Chuyển động thẳng biến đổi đều Soạn Lý 10 trang 40 sách Kết nối tri thức
Giải Vật lí 10 Bài 9 Kết nối tri thức giúp các em học sinh có thêm nhiều gợi ý tham khảo để trả lời các câu hỏi phần khởi động và 2 bài tập cuối bài Chuyển động thẳng biến đổi đều được chính xác dễ dàng hơn.
Vật lý 10 Kết nối tri thức Bài 9 hướng dẫn giải bài tập trong sách giáo khoa rất chi tiết, chính xác. Hy vọng rằng tài liệu sẽ giúp các em học sinh hiểu được kiến thức về chuyển động thẳng biến đổi đều. Đồng thời các thầy cô giáo, bậc phụ huynh có thể sử dụng tài liệu để hướng dẫn các em khi tự học. Vậy sau đây là trọn bộ tài liệu soạn Vật lí 10 bài 9 Kết nối tri thức mời các bạn lớp 10 cùng theo dõi. Ngoài ra các bạn xem thêm Bài tập chuyển động thẳng biến đổi đều.
Vật lí 10 Bài 9: Chuyển động thẳng biến đổi đều
Khởi động trang 40 Vật lí 10
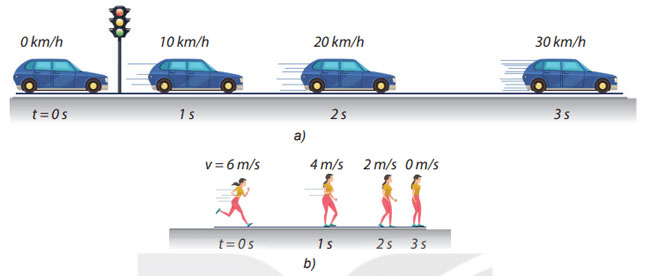
Hình trên mô tả sự thay đổi vị trí và vận tốc của ô tô, người sau những khoảng thời gian bằng nhau. Hai chuyển động này có gì giống nhau, khác nhau.
Gợi ý đáp án
- Giống: đều là chuyển động thẳng và có gia tốc không thay đổi.
- Khác nhau:
+ Chuyển động của ô tô có vận tốc tăng dần đều sau những khoảng thời gian bằng nhau nên đây là chuyển động nhanh dần đều.
+ Chuyển động của người có vận tốc giảm dần đều nên đây là chuyển động chậm dần đều.
Giải bài tập Vật lí 10 Bài 9
Bài 1 trang 43
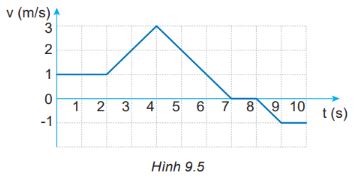
Đồ thị vận tốc – thời gian ở Hình 9.5 mô tả chuyển động của một chú chó con đang chạy trong ngõ thẳng và hẹp.
a) Hãy mô tả chuyển động của chú chó.
b) Tính quãng đường đi được và độ dịch chuyển của chú chó sau 2s; 4s; 7s và 10s bằng đồ thị và bằng công thức.
Gợi ý đáp án
a) Mô tả chuyển động:
- Từ giây thứ 0 đến giây thứ 2: chuyển động thẳng đều với vận tốc 1 m/s.
- Từ giây thứ 2 đến giây thứ 4: chuyển động thẳng nhanh dần đều từ 1 m/s đến 3 m/s.
- Từ giây thứ 4 đến giây thứ 7: chuyển động chậm dần đều từ 3 m/s về 0 m/s.
- Từ giây thứ 7 đến giây thứ 8: đứng yên.
- Từ giây thứ 8 đến giây thứ 9: chuyển động thẳng nhanh dần đều theo chiều ngược lại (theo chiều âm).
- Từ giây thứ 9 đến giây thứ 10: chuyển động thẳng đều theo chiều âm.
b) Tính quãng đường và độ dịch chuyển bằng đồ thị
- Sau 2 giây:
+ Quãng đường: s1 = 1.2 = 2m
+ Độ dịch chuyển: d1 = 1.2 = 2m
- Sau 4 giây:
+ Quãng đường: s2 = s1 + ![]() \(\frac12\).(1 + 3).2 = 6m
\(\frac12\).(1 + 3).2 = 6m
+ Độ dịch chuyển: d2 = d1 + ![]() \(\frac12\).(1 + 3).2 = 6m
\(\frac12\).(1 + 3).2 = 6m
- Sau 7 giây:
+ Quãng đường: s3 = s2 + ![]() \(\frac12\).3.3 = 10,5m
\(\frac12\).3.3 = 10,5m
+ Độ dịch chuyển: d3 = d2 + ![]() \(\frac12\).3.3 = 10,5m
\(\frac12\).3.3 = 10,5m
- Sau 10 giây:
+ Từ giây thứ 7 đến giây thứ 8 vật đứng yên nên quãng đường bằng 0.
+ Quãng đường: s4 = s3 + ![]() \(\frac12\).1.1 + 1.1 = 12m
\(\frac12\).1.1 + 1.1 = 12m
+ Độ dịch chuyển: d4 = d3 + ![]() \(\frac12\).(-1).1 + (-1).1 = 9m
\(\frac12\).(-1).1 + (-1).1 = 9m
Tính quãng đường và độ dịch chuyển bằng công thức:
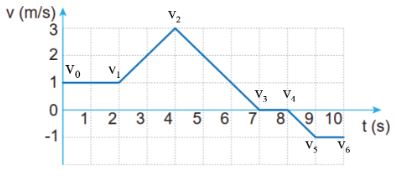
- Sau 2 giây:
+ Độ dịch chuyển: d1 = v0t1 = 1.2 = 2m
+ Vật chuyển động thẳng không đổi chiều nên quãng đường bằng độ dịch chuyển: s1 = d1 = 2m
- Sau 4 giây:
+ Gia tốc tính từ giây thứ 2 đến giây thứ 4: ![]() \(a_1\;=\;\frac{v_2\;-\;v_1}{4\;-\;2}\;=\;\frac{3-1}{4-2}\;=\;1\;m/s^2\)
\(a_1\;=\;\frac{v_2\;-\;v_1}{4\;-\;2}\;=\;\frac{3-1}{4-2}\;=\;1\;m/s^2\)
+ Độ dịch chuyển:
![]() \(d_2\;=\;d_1\;+\;v_1\;t_2\;+\;\frac12\;a_1\;t_2^2\;=\;2\;+\;1\;.\;2\;+\;\frac12\;.\;1\;.\;2^2\;=\;6\;m\)
\(d_2\;=\;d_1\;+\;v_1\;t_2\;+\;\frac12\;a_1\;t_2^2\;=\;2\;+\;1\;.\;2\;+\;\frac12\;.\;1\;.\;2^2\;=\;6\;m\)
+ Vật chuyển động thẳng không đổi chiều nên quãng đường bằng độ dịch chuyển: s2 = d2 = 6m
- Sau 7 giây:
+ Gia tốc tính từ giây thứ 4 đến giây thứ 7: ![]() \(a_2\;=\;\frac{v_3\;-\;v_2}{7\;-\;4}\;=\;\frac{0\;-\;3}{7\;-\;4}\;=\;-1\;m/s^2\)
\(a_2\;=\;\frac{v_3\;-\;v_2}{7\;-\;4}\;=\;\frac{0\;-\;3}{7\;-\;4}\;=\;-1\;m/s^2\)
+ Độ dịch chuyển: ![]() \(d_3\;=\;d_2\;+\;v_2\;t_3\;+\;\frac12\;a_2\;t_3^2\;=\;6\;+\;3\;.\;3\;+\;\frac12\;.\;(-1)\;.\;3^2\;=\;10,5\;m\)
\(d_3\;=\;d_2\;+\;v_2\;t_3\;+\;\frac12\;a_2\;t_3^2\;=\;6\;+\;3\;.\;3\;+\;\frac12\;.\;(-1)\;.\;3^2\;=\;10,5\;m\)
+ Vật chuyển động thẳng không đổi chiều nên quãng đường bằng độ dịch chuyển: s3 = d3 = 10,5m
- Sau 10 giây:
+ Từ giây thứ 7 đến giây thứ 8 vật đứng yên nên quãng đường bằng 0.
+ Từ giây thứ 8 đến giây thứ 9 vật chuyển động theo chiều âm
+ Gia tốc tính từ giây thứ 8 đến giây thứ 9: ![]() \(a_3\;=\;\frac{v_5\;-\;v_4}{9\;-\;8}\;=\;\frac{-\;1\;-\;0}{9\;-\;8}\;=\;-1\;m/s^2\)
\(a_3\;=\;\frac{v_5\;-\;v_4}{9\;-\;8}\;=\;\frac{-\;1\;-\;0}{9\;-\;8}\;=\;-1\;m/s^2\)
+ Độ dịch chuyển từ giây thứ 8 đến giây thứ 9: ![]() \(d_4\;=\;v_4\;t_5\;+\;\frac12\;a_3\;t_5^2\;=\;0\;.\;1\;+\;\frac12\;.\;(-1)\;.\;1^2\;=\;-\;0,5\;m\)
\(d_4\;=\;v_4\;t_5\;+\;\frac12\;a_3\;t_5^2\;=\;0\;.\;1\;+\;\frac12\;.\;(-1)\;.\;1^2\;=\;-\;0,5\;m\)
+ Quãng đường vật đi được từ giây thứ 8 đến giây thứ 9 là: s' = 0,5m
+ Từ giây thứ 9 đến giây thứ 10 vật chuyển động thẳng đều nên gia tốc bằng 0
+ Độ dịch chuyển từ giây thứ 9 đến giây thứ 10: d5 = v5t6 = (-1) . 1 = -1m
+ Quãng đường vật đi được từ giây thứ 9 đến giây thứ 10 là: s'' = 1m
+ Độ dịch chuyển sau 10 giây: d = d3 + d4 + d5 = 10,5 - 0,5 - 1 = 9m
+ Quãng đường sau 10 giây: s = s3 + s4 + s5 = 10,5 + 0,5 + 1 = 12m
Bài 2 trang 43
Một vận động viên đua xe đạp đường dài vượt qua vạch đích với tốc độ 10 m/s. Sau đó vận động viên này đi chậm dần đều thêm 20 m mới dừng lại. Coi chuyển động của vận động viên là thẳng.
a) Tính gia tốc của vận động viên trong đoạn đường sau khi qua vạch đích.
b) Tính thời gian vận động viên đó cần để dừng lại kể từ khi cán đích.
c) Tính vận tốc trung bình của người đó trên quãng đường dừng xe.
Gợi ý đáp án
a)
Áp dụng công thức: ![]() \(v^2\;-\;v_0^2\;=\;2ad\)
\(v^2\;-\;v_0^2\;=\;2ad\)
Gia tốc của vận động viên trong đoạn đường sau khi qua vạch đích (khi dừng lại v = 0) là
![]() \(a\;=\;\frac{v^2\;-\;v_0^2}{2d}\;=\;\frac{0^2\;-\;10^2}{2\;.\;20}\;=\;-\;2,5\;m/s^2\)
\(a\;=\;\frac{v^2\;-\;v_0^2}{2d}\;=\;\frac{0^2\;-\;10^2}{2\;.\;20}\;=\;-\;2,5\;m/s^2\)
b) Thời gian vận động viên cần để dựng lại kể từ khi cán đích là:
![]() \(t\;=\;\frac{v\;-\;v_0}a\;=\;\frac{0\;-\;10}{-\;2,5}\;=\;4s\)
\(t\;=\;\frac{v\;-\;v_0}a\;=\;\frac{0\;-\;10}{-\;2,5}\;=\;4s\)
c) Vận tốc trung bình của người đó trên quãng đường dừng xe là:
![]() \(v_{tb}\;=\;\frac{v\;+\;v_0}2\;=\;\frac{0\;+\;10}2\;=\;5\;m/s\)
\(v_{tb}\;=\;\frac{v\;+\;v_0}2\;=\;\frac{0\;+\;10}2\;=\;5\;m/s\)
Hoặc có thể áp dụng công thức: ![]() \(v_{tb}\hspace{0.278em}=\;\frac dt\;=\;\frac{20}4\;=\;5\;m/s\hspace{0.278em}\)
\(v_{tb}\hspace{0.278em}=\;\frac dt\;=\;\frac{20}4\;=\;5\;m/s\hspace{0.278em}\)
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:












 Toán 10 Kết nối tri thức
Toán 10 Kết nối tri thức
 Toán 10 Chân trời sáng tạo
Toán 10 Chân trời sáng tạo
 Toán 10 Cánh Diều
Toán 10 Cánh Diều
 Soạn văn 10 Chân trời sáng tạo
Soạn văn 10 Chân trời sáng tạo
 Soạn văn 10 Cánh Diều
Soạn văn 10 Cánh Diều
 Soạn văn 10 Kết nối tri thức
Soạn văn 10 Kết nối tri thức
 Tiếng Anh 10 Global Success
Tiếng Anh 10 Global Success
 Tiếng anh 10 Friends Global
Tiếng anh 10 Friends Global
 Tiếng Anh 10 Explore New Worlds
Tiếng Anh 10 Explore New Worlds









