Vật lí 10 Bài 13: Tổng hợp và phân tích lực. Cân bằng lực Soạn Lý 10 trang 56 sách Kết nối tri thức
Giải Vật lí 10 Bài 13: Tổng hợp và phân tích lực - Cân bằng lực sách Kết nối tri thức với cuộc sống giúp các em học sinh lớp 10 có thêm nhiều gợi ý tham khảo để biết cách trả lời các câu hỏi bài học Bài 13 trang 56 →59 thuộc chương 3: Động lực học.
Giải bài tập Vật lý 10 Bài 13: Tổng hợp và phân tích lực - Cân bằng lực giúp các em hiểu được kiến thức về phân tích lực, cân bằng lực ngang, từ đó sẽ trả lời toàn bộ các câu hỏi của Bài 13 chương III trong sách giáo khoa Vật lí 10 Kết nối tri thức với cuộc sống. Vậy sau đây là nội dung chi tiết bài Soạn Vật lí 10 Bài 13: Tổng hợp và phân tích lực - Cân bằng lực, mời các bạn cùng tải tại đây.
Vật lí 10 Bài 13: Tổng hợp và phân tích lực. Cân bằng lực
I. Tổng hợp lực – hợp lực tác dụng
Câu hỏi trang 56
Tại sao lực đẩy của người bố trong Hình 13.1b có tác dụng như lực đẩy của hai anh em?
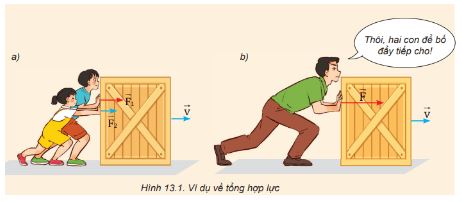
Gợi ý đáp án
Ở hình a: hai bé đẩy thùng với các lực ![]() \(\underset{F_{1} }{\rightarrow}\) và
\(\underset{F_{1} }{\rightarrow}\) và ![]() \(\underset{F_{2} }{\rightarrow}\) làm cho thùng chuyển động với vận tốc
\(\underset{F_{2} }{\rightarrow}\) làm cho thùng chuyển động với vận tốc ![]() \(\underset{v}{\rightarrow}\)
\(\underset{v}{\rightarrow}\)
Ở hình b: bố cũng đẩy chiếc thùng đó với lực ![]() \(\underset{F}{\rightarrow}\) và làm cho thùng cũng chuyển động với cùng vận tốc
\(\underset{F}{\rightarrow}\) và làm cho thùng cũng chuyển động với cùng vận tốc ![]() \(\underset{v}{\rightarrow}\).
\(\underset{v}{\rightarrow}\).
⇒ Lực đẩy của người bố có tác dụng như lực đẩy của hai anh em vì lực tác dụng của người bố làm cho chiếc thùng chuyển động cùng hướng với cùng vận tốc giống y hệt như trường hợp hai con đẩy thùng.
Câu hỏi 1 trang 57
Dựa vào Hình 13.2, hãy nêu cách xác định độ lớn và chiều của hợp lực trong hai trường hợp.
a) Vật chịu tác dụng của hai lực cùng phương, cùng chiều (Hình 13.2a).
b) Vật chịu tác dụng của hai lực cùng phương, ngược chiều (Hình 13.2b).
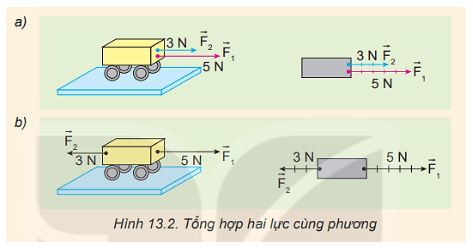
a) Vật chịu tác dụng của hai lực cùng phương, cùng chiều thì hợp lực có:
- Độ lớn bằng tổng hai lực thành phần F = F1 + F2
- Cùng chiều với hai lực thành phần.
b) Vật chịu tác dụng của hai lực cùng phương, ngược chiều thì hợp lực có:
- Độ lớn bằng trị tuyệt đối hiệu hai lực thành phần F = |F1 - F2|
- Cùng chiều với lực thành phần lớn hơn.
Câu hỏi 2 trang 57
Nêu quy tắc tổng hợp hai lực cùng phương.
Gợi ý đáp án
Lực tổng hợp của hai lực ![]() \(\underset{F_{1} }{\rightarrow}\) và
\(\underset{F_{1} }{\rightarrow}\) và ![]() \(\underset{F_{2} }{\rightarrow}\) là một lực
\(\underset{F_{2} }{\rightarrow}\) là một lực ![]() \(\underset{F}{\rightarrow}\) có:
\(\underset{F}{\rightarrow}\) có:
Trường hợp: hai lực thành phần cùng phương, cùng chiều
- Phương: cùng phương với hai lực thành phần.
- Chiều: cùng chiều với hai lực thành phần
- Độ lớn: F = F1 + F2
Trường hợp: hai lực thành phần cùng phương, ngược chiều
- Phương: cùng phương với hai lực thành phần.
- Chiều: ![]() \(\underset{F}{\rightarrow}\) cùng chiều với lực thành phần lớn hơn.
\(\underset{F}{\rightarrow}\) cùng chiều với lực thành phần lớn hơn.
- Độ lớn: F = |F1 - F2|
Câu hỏi 1 trang 58
Cho hai lực đồng quy có độ lớn F1 = 6 N và F2 = 8 N.
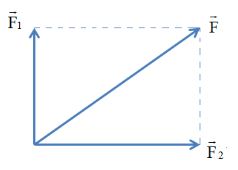
Nếu hợp lực có độ lớn F = 10 N thì góc giữa hai lực ![]() \(\underset{F_{1} }{\rightarrow}\) và
\(\underset{F_{1} }{\rightarrow}\) và ![]() \(\underset{F_{2} }{\rightarrow}\) bằng bao nhiêu? Vẽ hình minh họa.
\(\underset{F_{2} }{\rightarrow}\) bằng bao nhiêu? Vẽ hình minh họa.
Gợi ý đáp án
Để xác định được mối liên hệ về phương, chiều của các lực thành phần và hợp lực ta sẽ dựa vào các trường hợp đặc biệt:
- Hai lực thành phần cùng phương, cùng chiều thì: F = F1 + F2 nhưng 10 ≠ 6 + 8
- Hai lực thành phần cùng phương, ngược chiều thì: F = |F1 - F2| nhưng 10 ≠ |6 - 8|
- Hai lực thành phần hợp với nhau một góc nào đó, ta sẽ thường để ý đến các góc đặc biệt như góc 60°; 90°
Ta có: 10 = ![]() \(\sqrt{6^{2} + 8^{2} }\) hay F =
\(\sqrt{6^{2} + 8^{2} }\) hay F =![]() \(\sqrt{F_{1}^{2} + F_{2}^{2} }\)
\(\sqrt{F_{1}^{2} + F_{2}^{2} }\)
⇒ ![]() \(\underset{F_{1} }{\rightarrow}\)
\(\underset{F_{1} }{\rightarrow}\) ![]() \(\perp\)
\(\perp\) ![]() \(\underset{F_{2} }{\rightarrow}\) hay góc giữa hai lực
\(\underset{F_{2} }{\rightarrow}\) hay góc giữa hai lực ![]() \(\underset{F_{1} }{\rightarrow}\) và
\(\underset{F_{1} }{\rightarrow}\) và ![]() \(\underset{F_{2} }{\rightarrow}\) bằng 90°
\(\underset{F_{2} }{\rightarrow}\) bằng 90°
Câu hỏi 2 trang 57
Giả sử lực kéo của mỗi tàu kéo ở đầu bài đều có độ lớn bằng 8000 N và góc giữa hai dây cáp bằng 30o.
a) Biểu diễn các lực kéo của mỗi tàu và hợp lực tác dụng vào tàu chở hàng.
b) Tính độ lớn của hợp lực của hai lực kéo.
c) Xác định phương và chiều của hợp lực.
d) Nếu góc giữa hai dây cáp bằng 90o thì hợp lực của hai lực kéo có phương, chiều và độ lớn như thế nào?
Gợi ý đáp án
a.
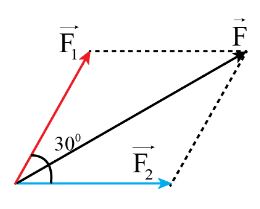
b) Áp dụng quy tắc hình bình hành ta có:
F = ![]() \(\sqrt{F_{1}^{2} + F_{2}^{2} + 2F_{1} F_{2} cos\alpha }\)
\(\sqrt{F_{1}^{2} + F_{2}^{2} + 2F_{1} F_{2} cos\alpha }\)
= ![]() \(\sqrt{8000^{2} + 8000^{2} + 2.8000.8000.cos 30^{0} }\)
\(\sqrt{8000^{2} + 8000^{2} + 2.8000.8000.cos 30^{0} }\)
c) Đặt tên các đỉnh cho hình trên
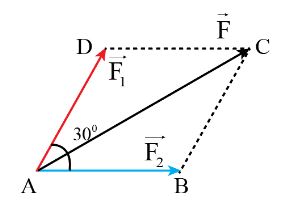
Xét ∆ABC có AB = BC (do hai lực thành phần F1 = F2 = 8000N) nên ∆ABC là tam giác cân tại B. Suy ra ![]() \(\widehat{CAB}\) =
\(\widehat{CAB}\) = ![]() \(\widehat{ACB}\)
\(\widehat{ACB}\)
Mặt khác ![]() \(\widehat{DAC\;}=\;\widehat{ACB}\) tính chất góc so le trong ở trong hình bình hành ABCD.
\(\widehat{DAC\;}=\;\widehat{ACB}\) tính chất góc so le trong ở trong hình bình hành ABCD.
⇒ ![]() \(\widehat{DAC}=\;\widehat{ACB}\;=\;\frac12\widehat{DAB}\;=\;15^0\)
\(\widehat{DAC}=\;\widehat{ACB}\;=\;\frac12\widehat{DAB}\;=\;15^0\)
Nên:
- Phương của hợp lực là phương xiên, hợp với phương nằm ngang một góc 15o
- Chiều của hợp lực hướng về phía trước.
Hoặc có thể sử dụng định lí hàm số cosin trong tam giác ABC cũng có thể tính được.
d) Nếu góc giữa hai dây cáp bằng 90o thì hợp lực của hai dây kéo có:
- Phương: phương xiên, hợp với phương nằm ngang một góc 45o
- Chiều: hướng về phía trước
- Độ lớn: ![]() \(F = \sqrt{F_{1}^{2} + F_{2}^{2} } = \sqrt{8000^{2} + 8000^{2} } \approx 1114N\)
\(F = \sqrt{F_{1}^{2} + F_{2}^{2} } = \sqrt{8000^{2} + 8000^{2} } \approx 1114N\)
II. Các lực cân bằng và không cân bằng
Câu hỏi trang 58
Quan sát quyển sách đang nằm yên trên mặt bàn (Hình 13.5)
a) Có những lực nào tác dụng lên quyển sách?
b) Các lực này có cân bằng không? Vì sao?

Gợi ý đáp án:
a) Các lực tác dụng lên quyển sách gồm: Trọng lực ![]() \(\vec{P}\) , phản lực
\(\vec{P}\) , phản lực ![]() \(\vec{N}\) của bàn.
\(\vec{N}\) của bàn.
b) Các lực này có cân bằng vì quyển sách nằm yên.
Câu hỏi 1 trang 58
Một ô tô chịu một lực F1 = 400N hướng về phía trước và một lực F2 = 300N hướng về phía sau (Hình 13.6). Hỏi hợp lực tác dụng lên ô tô có độ lớn bằng bao nhiêu và hướng về phía nào?
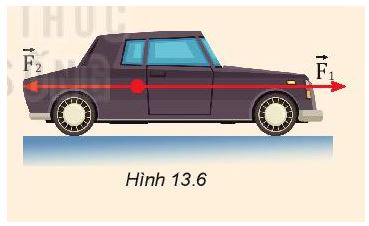
Gợi ý đáp án:
Ta thấy: ![]() \(\vec{F_{1} }\) ↑↓
\(\vec{F_{1} }\) ↑↓ ![]() \(\vec{F_{2} }\) ⇒ F = |F1− F2| = |400−300| = 100N
\(\vec{F_{2} }\) ⇒ F = |F1− F2| = |400−300| = 100N
Và có chiều hướng về phía trước.
Câu hỏi 2 trang 58
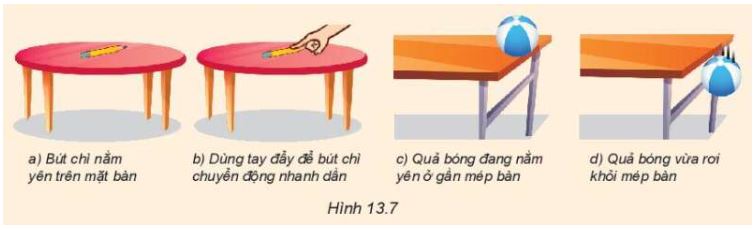
Quan sát cặp tình huống ở Hình 13.7.
a) Tình huống nào có hợp lực khác 0?
b) Mô tả sự thay đổi vận tốc (độ lớn, hướng) của mỗi vật trong hình, nếu có.
Gợi ý đáp án:
a)
Tình huống có hợp lực khác 0 là:
- Dùng tay đẩy để bút chì chuyển động nhanh dần
- Qủa bóng vừa rơi khỏi mép bàn.
b)
- Dùng tay đẩy để bút chì chuyển động nhanh dần: độ lớn vận tốc sẽ tăng dần, hướng chuyển động về phía trước.
- Quả bóng vừa rơi khỏi mép bàn: độ lớn vận tốc tăng dần, hướng chuyển động theo phương thẳng đứng hướng xuống.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:












 Toán 10 Kết nối tri thức
Toán 10 Kết nối tri thức
 Toán 10 Chân trời sáng tạo
Toán 10 Chân trời sáng tạo
 Toán 10 Cánh Diều
Toán 10 Cánh Diều
 Soạn văn 10 Chân trời sáng tạo
Soạn văn 10 Chân trời sáng tạo
 Soạn văn 10 Cánh Diều
Soạn văn 10 Cánh Diều
 Soạn văn 10 Kết nối tri thức
Soạn văn 10 Kết nối tri thức
 Tiếng Anh 10 Global Success
Tiếng Anh 10 Global Success
 Tiếng anh 10 Friends Global
Tiếng anh 10 Friends Global
 Tiếng Anh 10 Explore New Worlds
Tiếng Anh 10 Explore New Worlds









