Đề cương ôn tập học kì 1 môn Toán 7 sách Kết nối tri thức với cuộc sống Ôn tập cuối kì 1 Toán 7 năm 2024 - 2025 (Có đáp án)
Đề cương ôn tập học kì 1 Toán 7 Kết nối tri thức năm 2024 - 2025 gồm tóm tắt kiến thức kèm theo các dạng bài tập trọng tâm. Qua đó giúp các em học sinh hệ thống toàn bộ kiến thức trọng tâm trong chương trình học kì 1 giúp các em dễ dàng ôn tập.
Đề cương ôn tập Toán 7 học kì 1 có đáp án Kết nối tri thức bao gồm 10 trang có đáp án chi tiết kèm theo, giúp các bạn làm quen với các dạng bài tập, nâng cao kỹ năng làm bài để không còn bỡ ngỡ khi bước vào kì thi chính thức. Bên cạnh đó các bạn xem thêm đề cương ôn tập học kì 1 Khoa học tự nhiên 7 Kết nối tri thức, đề cương ôn tập học kì 1 Lịch sử Địa lí 7 Kết nối tri thức.
Đề cương ôn tập Toán 7 học kì 1 Kết nối tri thức 2024
|
PHÒNG GD&ĐT........... TRƯỜNG THCS............. |
ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 1 NĂM 2024 - 2025 MÔN TOÁN 7 KNTTVCS |
I. Lý thuyết ôn tập học kì 1
1. Số hữu tỉ Là số viết được dưới dạng ![]() \(\frac{a}{b}\)với
\(\frac{a}{b}\)với ![]() \(a, b \in Z, b \neq 0\). Tập hợp các số hữu tỉ được kí hiệu là Q .
\(a, b \in Z, b \neq 0\). Tập hợp các số hữu tỉ được kí hiệu là Q .
2. Số vô tỉ
* Căn bậc hai số học của số a không âm là số x không âm sao cho ![]() \(x^2=a.\)
\(x^2=a.\)
Ta đùng kí hiệu \sqrt{a} để chỉ căn bậc hai số học của số a .
Ví dụ:![]() \(\sqrt{4}=2 ; \sqrt{100}=10 ; \sqrt{0}=0\)
\(\sqrt{4}=2 ; \sqrt{100}=10 ; \sqrt{0}=0\)
* Một số không âm a có đúng một căn bậc hai số học.
Chú ý:
* Số âm không có căn bậc hai số học.
* Ta có ![]() \(\sqrt{a} \geq 0\) với mọi số không âm.
\(\sqrt{a} \geq 0\) với mọi số không âm.
* Với mọi số không âm a, ta luôn có ![]() \((\sqrt{a})^2=a.\)
\((\sqrt{a})^2=a.\)
Ví dụ: ![]() \((\sqrt{3})^2=3\)
\((\sqrt{3})^2=3\)
3. Lũy thừa bậc n của một số hữu tỉ x, kí hiệu ![]() \(x^n\), là tích của n thừa số x.
\(x^n\), là tích của n thừa số x.
![]() \(x^n=\underset{n \text { thas } s 0}{x x x_0} x(x \in Q, n \in N, n>1)\)
\(x^n=\underset{n \text { thas } s 0}{x x x_0} x(x \in Q, n \in N, n>1)\)
Quy ước: ![]() \(x^1=x ; x^0=1(x \neq 0)\)
\(x^1=x ; x^0=1(x \neq 0)\)
* Khi viết số hữu tỉ x dưới dạng ![]() \(\frac{a}{b}\) với
\(\frac{a}{b}\) với ![]() \(a, b \in Z, b \neq 0\), ta có:
\(a, b \in Z, b \neq 0\), ta có: ![]() \(\left(\frac{a}{b}\right)^n=\frac{a^n}{b^n}\)
\(\left(\frac{a}{b}\right)^n=\frac{a^n}{b^n}\)
4. Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng hai số mũ.
![]() \(x^m \cdot x^n=x^{m+n}\)
\(x^m \cdot x^n=x^{m+n}\)
5. Khi chia hai lũy thừa cùng cơ số khác 0 , ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị trừ đi số mũ của lũy thừa chia.
![]() \(x^m: x^n=x^{m-n}(x \neq 0 ; \mathrm{m} \geq \mathrm{n})\)
\(x^m: x^n=x^{m-n}(x \neq 0 ; \mathrm{m} \geq \mathrm{n})\)
.............
II. Các dạng bài tập trọng tâm
PHẦN I. TRẮC NGHIỆM
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:
Câu 1. Trong các câu sau, câu nào đúng?
A. Số hữu tỉ âm nhỏ hơn số hữu tỉ dương;
B. Số 0 là số hữu tỉ dương;
C.Số nguyên âm không phải là số hữu tỉ âm;
D. Tập hợp Q gồm các số hữu tỉ dương và các số hữu tỉ âm.
Câu 2. Trong các số sau, số nào biểu diễn số đối của số hữu tỉ –0,5?
A. 1/2;
B. −1/2;
C. 2;
D. –2.
Câu 3. Số ![]() \(-\frac{1}{3}\) là số:
\(-\frac{1}{3}\) là số:
A. Số thập phân vô hạn không tuần hoàn;
B. Số thập phân hữu hạn;
C. Số thập phân vô hạn tuần hoàn;
D. Số vô tỉ.
Câu 4. ![]() \(\sqrt{64}\) bằng:
\(\sqrt{64}\) bằng:
A. ± 8;
B. –8;
C. 8;
D. 64.
Câu 5. Nếu |x| = 2 thì:
A. x = 2;
B. x = –2;
C. x = 2 hoặc x = –2;
D. Không có giá trị nào của x thỏa mãn.
Câu 6. Quan sát hình vẽ.
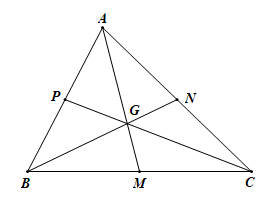
Có tất cả bao nhiêu góc kề bù với ![]() \(\hat{NGC}\)?
\(\hat{NGC}\)?
A. 1;
B. 2;
C. 3;
D. 4.
Câu 7. Trong các câu sau, câu nào không phải định lí?
A. Nếu hai góc bằng nhau thì chúng đối đỉnh;
B. Nếu hai góc kề bù thì tổng số đo của chúng bằng 180°;
C. Nếu hai góc bù nhau thì tổng số đo của chúng bằng 180°;
D. Nếu hai góc đối đỉnh thì chúng bằng nhau.
Câu 8. Tổng số đo ba góc của một tam giác là
A. 45°;
B. 60°;
C. 90°;
D. 180°.
Câu 9. Phát biểu nào dưới đây là sai?
A. Hai tam giác có các góc tương ứng bằng nhau là hai tam giác bằng nhau;
B. Hai tam giác bằng nhau thì có các góc tương ứng bằng nhau;
C. Hai tam giác có các góc tương ứng bằng nhau, các cạnh tương ứng bằng nhau thì hai tam giác đó bằng nhau.
D. Hai tam giác bằng nhau là hai tam giác có các cạnh bằng nhau và có các góc bằng nhau.
Câu 10. Cho các hình vẽ sau:
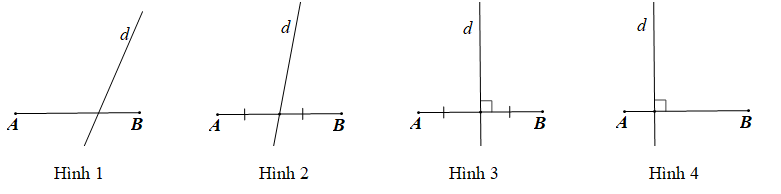
Hình vẽ nào minh họa đường thẳng d là đường trung trực của đoạn thẳng AB?
A. Hình 1;
B. Hình 2;
C. Hình 3;
D. Hình 4.
Câu 11. Thân nhiệt (°C) của bạn An trong cùng khung giờ 7h sáng các ngày trong tuần được ghi lại trong bảng sau:

Bạn An đã thu được dữ liệu trên bằng cách nào?
A. Xem tivi;
B. Lập bảng hỏi;
C. Ghi chép số liệu thống kê hằng ngày;
D. Thu thập từ các nguồn có sẵn như: sách, báo, web.
Câu 12. Kết quả tìm hiểu về khả năng chơi cầu lông của các bạn học sinh nam lớp 7C cho bởi bảng thống kê sau:

Kết quả tìm hiểu về khả năng chơi bóng đá của các bạn học sinh nữ của lớp 7C được cho bởi bảng thống kê sau:

Khẳng định nào dưới đây là đúng?
A. Dữ liệu về khả năng chơi cầu lông của các bạn học sinh nam lớp 7C đại diện cho khả năng chơi cầu lông học sinh cả lớp 7C;
B. Dữ liệu về khả năng chơi bóng đá của các bạn học sinh nữ lớp 7C đại diện cho khả năng chơi cầu lông học sinh cả lớp 7C;
C. Dữ liệu về khả năng chơi cầu lông và bóng đá được thống kê chưa đủ đại diện cho khả năng chơi thể thao của các bạn lớp 7C;
D. Lớp 7C có 35 học sinh.
Câu 13. Số hữu tỉ là số viết được dưới dạng phân số a/b với:
A. a = 0, b ≠ 0;
B. a, b ∈ ℤ; b ≠ 0;
C. a, b ∈ ℕ;
D. a ∈ ℕ; ; b ≠ 0.
Câu 14: Trong các số sau, số nào viết được dưới dạng số thập phân vô hạn tuần hoàn?
|
A. 10 |
B. |
|
C. |
D. |
Câu 15: Phát biểu nào dưới đây sai?
|
A. Số |
B. Số -2 là một số nguyên âm |
|
C. Số 19 là một số tự nhiên |
D. |
Câu 16. Căn bậc hai số học của số a không âm là:
A. √ a ;
B. − √ a ;
C. √ a và − √ a
D. Không có đáp án.
Câu 17. Nhận định nào sau đây là đúng?
A. 1,516 < 1,(516);
B. 1,516 = 1,(516);
C. 1,516 > 1,(516);
D. 1,516 ≈ 1,(516).
Câu 18: Tính số đo của góc x trong hình vẽ dưới đây:
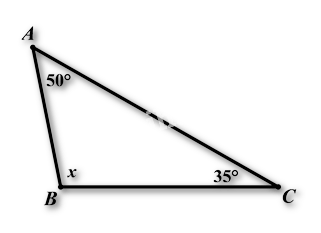
A. x = ![]() \({85^0}\)
\({85^0}\)
B. x = ![]() \({110^0}\)
\({110^0}\)
C. x = ![]() \({115^0}\)
\({115^0}\)
D. x = ![]() \({95^0}\)
\({95^0}\)
Câu 19: Cho ![]() \(\Delta ABC = \Delta DEF\). Biết
\(\Delta ABC = \Delta DEF\). Biết ![]() \(\angle A = {33^0}\). Khi đó:
\(\angle A = {33^0}\). Khi đó:
A. ![]() \(\angle D = {33^0}\)
\(\angle D = {33^0}\)
B. ![]() \(\angle D = {42^0}\)
\(\angle D = {42^0}\)
C. ![]() \(\angle E = {32^0}\)
\(\angle E = {32^0}\)
D. ![]() \(\angle D = {66^0}\)
\(\angle D = {66^0}\)
Câu 20: Số tam giác cân trong hình vẽ dưới đây là:
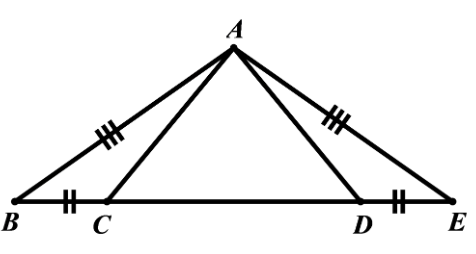
A. 2
B. 1
C. 4
D. 3
Câu 21 Đường trung trực của đoạn thẳng AB là đường thẳng …
A. song song với đoạn thẳng AB.
B. vuông góc với đoạn thẳng AB.
C. đi qua trung điểm của đoạn thẳng AB.
D. vuông góc với đoạn thẳng AB tại trung điểm của nó.
Câu 22. Điền vào chỗ chấm:
Đường thẳng … một đoạn thẳng tại … của nó được gọi là đường trung trực của đoạn thẳng ấy.
A. vuông góc với, một điểm;
B. cắt, một điểm;
C. cắt, trung điểm;
D. vuông góc với, trung điểm.
Câu 23 Dãy dữ liệu về cân nặng (đơn vị: kilôgam) của 7 học sinh lớp 7A: 25; 30; 32; 28; 29; 31; 27 thuộc loại dữ liệu nào?
A. Dữ liệu không là số;
B. Dữ liệu định tính;
C. Dữ liệu định lượng;
D. Dữ liệu kilôgam.
Câu 24 Thầy giáo muốn điều tra môn thể thao yêu thích của học sinh khối lớp 7 (gồm ba lớp 7A, 7B, 7C). Cách điều tra nào sau đây đảm bảo được tính đại diện?
A. Lấy ý kiến của các bạn nam;
B. Lấy ý kiến của các bạn nữ;
C. Lấy ý kiến của các bạn lớp 7A;
D. Lấy ý kiến ngẫu nhiên của các bạn trong cả ba lớp 7A, 7B, 7C.
Phần II. Tự luận
Bài 1:
Thực hiện phép tính:
a) ![]() \(\left( { - \dfrac{3}{4} + \dfrac{2}{3}} \right):\dfrac{5}{{11}} + \left( { - \dfrac{1}{4} + \dfrac{1}{3}} \right):\dfrac{5}{{11}}\)
\(\left( { - \dfrac{3}{4} + \dfrac{2}{3}} \right):\dfrac{5}{{11}} + \left( { - \dfrac{1}{4} + \dfrac{1}{3}} \right):\dfrac{5}{{11}}\)
b) ![]() \(\dfrac{{{{27}^{10}}{{.16}^{25}}}}{{{6^{30}}{{.32}^{15}}}}\)
\(\dfrac{{{{27}^{10}}{{.16}^{25}}}}{{{6^{30}}{{.32}^{15}}}}\)
c)  \(\left| {\dfrac{3}{5} - \dfrac{1}{{10}}} \right| - \sqrt {\dfrac{{36}}{{25}}} + {\left( {\dfrac{3}{{10}}} \right)^5}:{\left( {\dfrac{3}{{10}}} \right)^4}\)
\(\left| {\dfrac{3}{5} - \dfrac{1}{{10}}} \right| - \sqrt {\dfrac{{36}}{{25}}} + {\left( {\dfrac{3}{{10}}} \right)^5}:{\left( {\dfrac{3}{{10}}} \right)^4}\)
d) ![]() \(\sqrt {144} + \sqrt {49} - 10\sqrt {\dfrac{4}{{25}}}\)
\(\sqrt {144} + \sqrt {49} - 10\sqrt {\dfrac{4}{{25}}}\)
Bài 2:
Tìm x, biết:
a) ![]() \(\left( { - \dfrac{1}{2}} \right) + \left( {\dfrac{4}{5} + x} \right) = 1\dfrac{1}{2}\)
\(\left( { - \dfrac{1}{2}} \right) + \left( {\dfrac{4}{5} + x} \right) = 1\dfrac{1}{2}\)
b)  \({\left( {x - \dfrac{1}{3}} \right)^2} = \dfrac{1}{9}\)
\({\left( {x - \dfrac{1}{3}} \right)^2} = \dfrac{1}{9}\)
c) ![]() \(5.\sqrt x - \sqrt {\dfrac{1}{{25}}} = 0\)
\(5.\sqrt x - \sqrt {\dfrac{1}{{25}}} = 0\)
d) ![]() \(\left| {0,3 - x} \right| = \dfrac{1}{3}\)
\(\left| {0,3 - x} \right| = \dfrac{1}{3}\)
Bài 3:
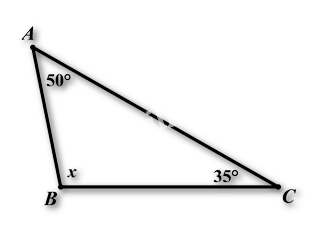
Tính số đo của góc x trong hình vẽ dưới đây:
Bài 4
Cho tam giác ABC cân tại A có ![]() \(\widehat {A{\rm{ }}} = 120^\circ\). Trên cạnh BC lấy hai điểm M, N sao cho MA, NA lần lượt vuông góc với AB, AC. Chứng minh rằng:
\(\widehat {A{\rm{ }}} = 120^\circ\). Trên cạnh BC lấy hai điểm M, N sao cho MA, NA lần lượt vuông góc với AB, AC. Chứng minh rằng:
a) ![]() \(\Delta BAM = \Delta CAN\);
\(\Delta BAM = \Delta CAN\);
b) Các tam giác ANB, AMC lần lượt cân tại N, M.
Bài 5:
Tìm số thực x, biết: ![]() \(\left| x \right| + \left| {x + 2} \right| = 0\).
\(\left| x \right| + \left| {x + 2} \right| = 0\).
ĐÁP ÁN ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 1 TOÁN 7
PHẦN I. TRẮC NGHIỆM
|
Câu |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Đáp án |
A |
A |
C |
C |
B |
B |
A |
D |
A |
C |
C |
C |
|
Câu |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
|
Đáp án |
B |
D |
A |
A |
A |
D |
A |
A |
D |
C |
C |
D |
Phần II. Tự luận:
Bài 1
a) ![]() \(\left( { - \dfrac{3}{4} + \dfrac{2}{3}} \right):\dfrac{5}{{11}} + \left( { - \dfrac{1}{4} + \dfrac{1}{3}} \right):\dfrac{5}{{11}}\)
\(\left( { - \dfrac{3}{4} + \dfrac{2}{3}} \right):\dfrac{5}{{11}} + \left( { - \dfrac{1}{4} + \dfrac{1}{3}} \right):\dfrac{5}{{11}}\)
![\begin{array}{l} = \left( { - \dfrac{3}{4} + \dfrac{2}{3}} \right).\dfrac{{11}}{5} + \left( { - \dfrac{1}{4} + \dfrac{1}{3}} \right).\dfrac{{11}}{5}\\ = \left( { - \dfrac{3}{4} + \dfrac{2}{3} + \dfrac{{ - 1}}{4} + \dfrac{1}{3}} \right).\dfrac{{11}}{5}\\ = \left[ {\left( { - \dfrac{3}{4} + \dfrac{{ - 1}}{4}} \right) + \left( {\dfrac{2}{3} + \dfrac{1}{3}} \right)} \right].\dfrac{{11}}{5}\\ = \left( {\dfrac{{ - 4}}{4} + \dfrac{3}{3}} \right).\dfrac{{11}}{5}\\ = \left( { - 1 + 1} \right).\dfrac{{11}}{5}\\ = 0.\dfrac{{11}}{5} = 0\end{array}](https://st.download.vn/data/image/blank.png) \(\begin{array}{l} = \left( { - \dfrac{3}{4} + \dfrac{2}{3}} \right).\dfrac{{11}}{5} + \left( { - \dfrac{1}{4} + \dfrac{1}{3}} \right).\dfrac{{11}}{5}\\ = \left( { - \dfrac{3}{4} + \dfrac{2}{3} + \dfrac{{ - 1}}{4} + \dfrac{1}{3}} \right).\dfrac{{11}}{5}\\ = \left[ {\left( { - \dfrac{3}{4} + \dfrac{{ - 1}}{4}} \right) + \left( {\dfrac{2}{3} + \dfrac{1}{3}} \right)} \right].\dfrac{{11}}{5}\\ = \left( {\dfrac{{ - 4}}{4} + \dfrac{3}{3}} \right).\dfrac{{11}}{5}\\ = \left( { - 1 + 1} \right).\dfrac{{11}}{5}\\ = 0.\dfrac{{11}}{5} = 0\end{array}\)
\(\begin{array}{l} = \left( { - \dfrac{3}{4} + \dfrac{2}{3}} \right).\dfrac{{11}}{5} + \left( { - \dfrac{1}{4} + \dfrac{1}{3}} \right).\dfrac{{11}}{5}\\ = \left( { - \dfrac{3}{4} + \dfrac{2}{3} + \dfrac{{ - 1}}{4} + \dfrac{1}{3}} \right).\dfrac{{11}}{5}\\ = \left[ {\left( { - \dfrac{3}{4} + \dfrac{{ - 1}}{4}} \right) + \left( {\dfrac{2}{3} + \dfrac{1}{3}} \right)} \right].\dfrac{{11}}{5}\\ = \left( {\dfrac{{ - 4}}{4} + \dfrac{3}{3}} \right).\dfrac{{11}}{5}\\ = \left( { - 1 + 1} \right).\dfrac{{11}}{5}\\ = 0.\dfrac{{11}}{5} = 0\end{array}\)
b)![]() \(\dfrac{{{{27}^{10}}{{.16}^{25}}}}{{{6^{30}}{{.32}^{15}}}}\)
\(\dfrac{{{{27}^{10}}{{.16}^{25}}}}{{{6^{30}}{{.32}^{15}}}}\)
 \(\begin{array}{l} = \dfrac{{{{\left( {{3^3}} \right)}^{10}}.{{\left( {{2^4}} \right)}^{25}}}}{{{{\left( {2.3} \right)}^{30}}.{{\left( {{2^5}} \right)}^{15}}}} = \dfrac{{{3^{3.10}}{{.2}^{4.25}}}}{{{2^{30}}{{.3}^{30}}{{.2}^{5.15}}}}\\ = \dfrac{{{3^{30}}{{.2}^{100}}}}{{{2^{30}}{{.3}^{30}}{{.2}^{75}}}} = \dfrac{{{2^{100}}}}{{{2^{30 + 75}}}}\\ = \dfrac{{{2^{100}}}}{{{2^{105}}}} = \dfrac{1}{{{2^5}}} = \dfrac{1}{{32}}\end{array}\)
\(\begin{array}{l} = \dfrac{{{{\left( {{3^3}} \right)}^{10}}.{{\left( {{2^4}} \right)}^{25}}}}{{{{\left( {2.3} \right)}^{30}}.{{\left( {{2^5}} \right)}^{15}}}} = \dfrac{{{3^{3.10}}{{.2}^{4.25}}}}{{{2^{30}}{{.3}^{30}}{{.2}^{5.15}}}}\\ = \dfrac{{{3^{30}}{{.2}^{100}}}}{{{2^{30}}{{.3}^{30}}{{.2}^{75}}}} = \dfrac{{{2^{100}}}}{{{2^{30 + 75}}}}\\ = \dfrac{{{2^{100}}}}{{{2^{105}}}} = \dfrac{1}{{{2^5}}} = \dfrac{1}{{32}}\end{array}\)
c)  \(\left| {\dfrac{3}{5} - \dfrac{1}{{10}}} \right| - \sqrt {\dfrac{{36}}{{25}}} + {\left( {\dfrac{3}{{10}}} \right)^5}:{\left( {\dfrac{3}{{10}}} \right)^4}\)
\(\left| {\dfrac{3}{5} - \dfrac{1}{{10}}} \right| - \sqrt {\dfrac{{36}}{{25}}} + {\left( {\dfrac{3}{{10}}} \right)^5}:{\left( {\dfrac{3}{{10}}} \right)^4}\)
 \(\begin{array}{l} = \left| {\dfrac{6}{{10}} - \dfrac{1}{{10}}} \right| - \dfrac{6}{5} + {\left( {\dfrac{3}{{10}}} \right)^{5 - 4}}\\ = \left| {\dfrac{5}{{10}}} \right| - \dfrac{6}{5} + {\left( {\dfrac{3}{{10}}} \right)^1}\\ = \dfrac{5}{{10}} - \dfrac{{12}}{{10}} + \dfrac{3}{{10}}\\ = \dfrac{{ - 4}}{{10}} = \dfrac{{ - 2}}{5}\end{array}\)
\(\begin{array}{l} = \left| {\dfrac{6}{{10}} - \dfrac{1}{{10}}} \right| - \dfrac{6}{5} + {\left( {\dfrac{3}{{10}}} \right)^{5 - 4}}\\ = \left| {\dfrac{5}{{10}}} \right| - \dfrac{6}{5} + {\left( {\dfrac{3}{{10}}} \right)^1}\\ = \dfrac{5}{{10}} - \dfrac{{12}}{{10}} + \dfrac{3}{{10}}\\ = \dfrac{{ - 4}}{{10}} = \dfrac{{ - 2}}{5}\end{array}\)
d) ![]() \(\sqrt {144} + \sqrt {49} - 10\sqrt {\dfrac{4}{{25}}}\)
\(\sqrt {144} + \sqrt {49} - 10\sqrt {\dfrac{4}{{25}}}\)
 \(\begin{array}{l} = 12 + 7 - 10.\dfrac{2}{5}\\ = 19 - 4\\ = 15\end{array}\)
\(\begin{array}{l} = 12 + 7 - 10.\dfrac{2}{5}\\ = 19 - 4\\ = 15\end{array}\)
Bài 2
a) ![]() \(\left( { - \dfrac{1}{2}} \right) + \left( {\dfrac{4}{5} + x} \right) = 1\dfrac{1}{2}\)
\(\left( { - \dfrac{1}{2}} \right) + \left( {\dfrac{4}{5} + x} \right) = 1\dfrac{1}{2}\)
 \(\begin{array}{l} - \dfrac{1}{2} + \dfrac{4}{5} + x = \dfrac{3}{2}\\x = \dfrac{3}{2} - \left( { - \dfrac{1}{2}} \right) - \dfrac{4}{5}\\x = \dfrac{3}{2} + \dfrac{1}{2} - \dfrac{4}{5}\\x = \dfrac{4}{2} - \dfrac{4}{5}\\x = 2 - \dfrac{4}{5}\\x = \dfrac{{10}}{5} - \dfrac{4}{5}\\x = \dfrac{6}{5}\end{array}\)
\(\begin{array}{l} - \dfrac{1}{2} + \dfrac{4}{5} + x = \dfrac{3}{2}\\x = \dfrac{3}{2} - \left( { - \dfrac{1}{2}} \right) - \dfrac{4}{5}\\x = \dfrac{3}{2} + \dfrac{1}{2} - \dfrac{4}{5}\\x = \dfrac{4}{2} - \dfrac{4}{5}\\x = 2 - \dfrac{4}{5}\\x = \dfrac{{10}}{5} - \dfrac{4}{5}\\x = \dfrac{6}{5}\end{array}\)
Vậy ![]() \(x = \dfrac{6}{5}\)
\(x = \dfrac{6}{5}\)
b)  \({\left( {x - \dfrac{1}{3}} \right)^2} = \dfrac{1}{9}\)
\({\left( {x - \dfrac{1}{3}} \right)^2} = \dfrac{1}{9}\)
 \({\left( {x - \dfrac{1}{3}} \right)^2} = {\left( {\dfrac{1}{3}} \right)^2} = {\left( { - \dfrac{1}{3}} \right)^2}\)
\({\left( {x - \dfrac{1}{3}} \right)^2} = {\left( {\dfrac{1}{3}} \right)^2} = {\left( { - \dfrac{1}{3}} \right)^2}\)
|
Trường hợp 1:
|
Trường hợp 2:
|
Vậy ![]() \(x \in \left\{ {\dfrac{2}{3};0} \right\}\)
\(x \in \left\{ {\dfrac{2}{3};0} \right\}\)
c) ![]() \(5.\sqrt x - \sqrt {\dfrac{1}{{25}}} = 0\)
\(5.\sqrt x - \sqrt {\dfrac{1}{{25}}} = 0\)
 \(\begin{array}{l}5.\sqrt x - \dfrac{1}{5} = 0\\5.\sqrt x = \dfrac{1}{5}\\\sqrt x = \dfrac{1}{5}:5 = \dfrac{1}{5}.\dfrac{1}{5} = \dfrac{1}{{25}}\end{array}\)
\(\begin{array}{l}5.\sqrt x - \dfrac{1}{5} = 0\\5.\sqrt x = \dfrac{1}{5}\\\sqrt x = \dfrac{1}{5}:5 = \dfrac{1}{5}.\dfrac{1}{5} = \dfrac{1}{{25}}\end{array}\)
 \(\begin{array}{l}\sqrt x = \sqrt {{{\left( {\dfrac{1}{{25}}} \right)}^2}} \\ \Rightarrow x = \dfrac{1}{{625}}\end{array}\)
\(\begin{array}{l}\sqrt x = \sqrt {{{\left( {\dfrac{1}{{25}}} \right)}^2}} \\ \Rightarrow x = \dfrac{1}{{625}}\end{array}\)
Vậy ![]() \(x = \dfrac{1}{{625}}\)
\(x = \dfrac{1}{{625}}\)
d) ![]() \(\left| {0,3 - x} \right| = \dfrac{1}{3}\)
\(\left| {0,3 - x} \right| = \dfrac{1}{3}\)
![]() \(\left| {\dfrac{3}{{10}} - x} \right| = \dfrac{1}{3}\)
\(\left| {\dfrac{3}{{10}} - x} \right| = \dfrac{1}{3}\)
|
Trường hợp 1:
Vậy |
Trường hợp 2:
|
Bài 3:
Xét ![]() \(\Delta ABC có: \angle A + \angle B + \angle C = {180^0}\) (định lý tổng ba góc trong một tam giác)
\(\Delta ABC có: \angle A + \angle B + \angle C = {180^0}\) (định lý tổng ba góc trong một tam giác)
 \(\begin{array}{l} \Rightarrow {50^0} + x + {35^0} = {180^0}\\ \Rightarrow x + {85^0} = {180^0}\\ \Rightarrow x = {180^0} - {85^0}\\ \Rightarrow x = {95^0}\end{array}\)
\(\begin{array}{l} \Rightarrow {50^0} + x + {35^0} = {180^0}\\ \Rightarrow x + {85^0} = {180^0}\\ \Rightarrow x = {180^0} - {85^0}\\ \Rightarrow x = {95^0}\end{array}\)
Vậy ![]() \(x = {95^0}\)
\(x = {95^0}\)
Bài 4
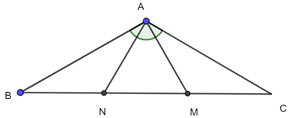
a) Xét 2 tam giác vuông BAM và CAN có:
AB=AC (Do tam giác ABC cân tại A)
![]() \(\widehat B = \widehat C\) (Do tam giác ABC cân tại A)
\(\widehat B = \widehat C\) (Do tam giác ABC cân tại A)
![]() \(=>\Delta BAM = \Delta CAN(g.c.g)\)
\(=>\Delta BAM = \Delta CAN(g.c.g)\)
b)
Xét tam giác ABC cân tại A, có ![]() \(\widehat {A{\rm{ }}} = 120^\circ\)có:
\(\widehat {A{\rm{ }}} = 120^\circ\)có:
![]() \(\widehat B = \widehat C = \frac{{{{180}^o} - {{120}^o}}}{2} = {30^o}\).
\(\widehat B = \widehat C = \frac{{{{180}^o} - {{120}^o}}}{2} = {30^o}\).
Xét tam giác ABM vuông tại A có:
 \(\begin{array}{l}\widehat B + \widehat {BAM} + \widehat {AMB} = {180^o}\\ \Rightarrow {30^o} + {90^o} + \widehat {AMB} = {180^o}\\ \Rightarrow \widehat {AMB} = {60^o}\\ \Rightarrow \widehat {AMC} = {180^o} - \widehat {AMB} = {180^o} - {60^o} = {120^o}\end{array}\)
\(\begin{array}{l}\widehat B + \widehat {BAM} + \widehat {AMB} = {180^o}\\ \Rightarrow {30^o} + {90^o} + \widehat {AMB} = {180^o}\\ \Rightarrow \widehat {AMB} = {60^o}\\ \Rightarrow \widehat {AMC} = {180^o} - \widehat {AMB} = {180^o} - {60^o} = {120^o}\end{array}\)
Xét tam giác MAC có:
 \(\begin{array}{l}\widehat {AMC} + \widehat {MAC} + \widehat C = {180^o}\\ \Rightarrow {120^o} + \widehat {MAC} + {30^o} = {180^o}\\ \Rightarrow \widehat {MAC} = {30^o} = \widehat C\end{array}\)
\(\begin{array}{l}\widehat {AMC} + \widehat {MAC} + \widehat C = {180^o}\\ \Rightarrow {120^o} + \widehat {MAC} + {30^o} = {180^o}\\ \Rightarrow \widehat {MAC} = {30^o} = \widehat C\end{array}\)
![]() \(\Rightarrow\)Tam giác AMC cân tại M.
\(\Rightarrow\)Tam giác AMC cân tại M.
Vì ![]() \(\Delta BAM = \Delta CAN=>BM=CN => BN=MC\)
\(\Delta BAM = \Delta CAN=>BM=CN => BN=MC\)
Xét 2 tam giác ANB và AMC có:
AB=AC
![]() \(AN = AM(do \Delta BAM = \Delta CAN)\)
\(AN = AM(do \Delta BAM = \Delta CAN)\)
BN=MC
![]() \(=>\Delta ANB = \Delta AMC(c.c.c)\)
\(=>\Delta ANB = \Delta AMC(c.c.c)\)
Mà tam giác AMC cân tại M.
=> Tam giác ANB cân tại N.
Bài 5
Do ![]() \(\left| x \right| \ge 0;\left| {x + 2} \right| \ge 0\) với mọi số thực x nên
\(\left| x \right| \ge 0;\left| {x + 2} \right| \ge 0\) với mọi số thực x nên ![]() \(\left| x \right| + \left| {x + 2} \right| \ge 0\) với mọi số thực x.
\(\left| x \right| + \left| {x + 2} \right| \ge 0\) với mọi số thực x.
Do đó, ![]() \(\left| x \right| + \left| {x + 2} \right| = 0\) khi
\(\left| x \right| + \left| {x + 2} \right| = 0\) khi ![]() \(\left| x \right| = 0\) và
\(\left| x \right| = 0\) và ![]() \(\left| {x + 2} \right| = 0\).
\(\left| {x + 2} \right| = 0\).
Suy ra x đồng thời bằng 0 và bằng - 2 (vô lí).
Vậy không có giá trị nào của x thỏa mãn yêu cầu của đề bài.
Chọn file cần tải:
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
-
 hcjkhfbThích · Phản hồi · 0 · 16/12/22
hcjkhfbThích · Phản hồi · 0 · 16/12/22-
 Thảo NhiThích · Phản hồi · 0 · 17/12/22
Thảo NhiThích · Phản hồi · 0 · 17/12/22
-












 Toán 7 Kết nối tri thức
Toán 7 Kết nối tri thức
 Toán 7 Chân trời sáng tạo
Toán 7 Chân trời sáng tạo
 Toán 7 Cánh Diều
Toán 7 Cánh Diều
 Soạn Văn 7 Chân trời sáng tạo
Soạn Văn 7 Chân trời sáng tạo
 Soạn Văn 7 Cánh Diều
Soạn Văn 7 Cánh Diều
 Soạn Văn 7 Kết nối tri thức
Soạn Văn 7 Kết nối tri thức
 Tiếng Anh 7 Global Success
Tiếng Anh 7 Global Success
 Tiếng Anh 7 Explore English
Tiếng Anh 7 Explore English
 Tiếng Anh 7 - iLearn Smart World
Tiếng Anh 7 - iLearn Smart World









