Công thức tính thể tích khối tròn xoay Công thức thể tích khối tròn xoay

Tải về

Khối tròn xoay là gì? Công thức tính khối tròn xoay như thế nào? Đây là câu hỏi được rất nhiều bạn học sinh quan tâm? Vì thế hãy cùng Eballsviet.com theo dõi bài viết dưới đây.

Trong bài viết dưới đây Eballsviet.com sẽ giới thiệu đến các bạn toàn bộ kiến thức về cách tính thể tích khối tròn xoay kèm theo một số ví dụ minh họa có đáp án giải chi tiết. Thông qua tài liệu này giúp các bạn học sinh có thêm nhiều tư liệu ôn tập, củng cố kiến thức làm quen với các dạng bài tập Hình học. Bên cạnh đó các bạn xem thêm công thức tính chu vi hình chữ nhật, công thức tính diện tích hình vuông.

Công thức tính thể tích khối tròn xoay

1. Khối tròn xoay là gì?

Trong không gian, khối tròn xoay là một khối hình được tạo bằng cách quay một mặt phẳng quanh một trục cố định.

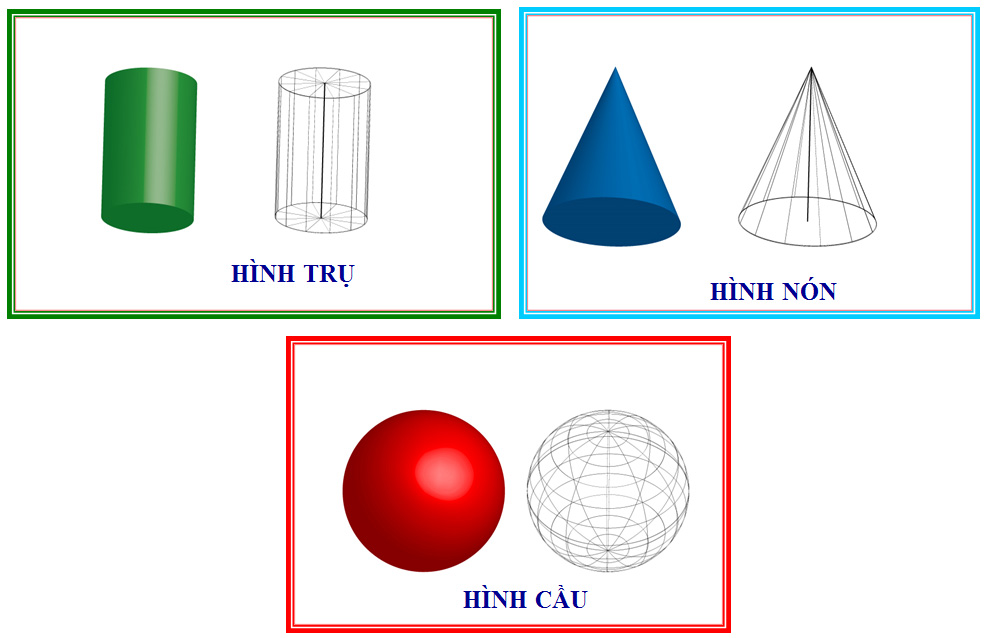
Trong chương trình toán học phổ thông các bạn sẽ được tiếp xúc với một số khối tròn xoay như khối nón tròn xoay, khối trụ tròn xoay, khối cầu tròn xoay,...

2. Tính thể tích khối tròn xoay quanh trục ox

Nếu khối tròn xoay quanh trục Ox thì để tính thể tích khối tròn xoay có thể áp dụng các công thức sau:

Trường hợp 1: Khối tròn xoay tạo bởi

Đường thẳng y=f(x)
Trục hoành $\mathrm{y}=0$ $\mathrm{y}=0$
x=a ; x=b

Khi đó công thức tính thể tích sẽ là:

$V=\pi \int_{a}^{b} f^{2}(x) d x$ $V=\pi \int_{a}^{b} f^{2}(x) d x$

Trường hợp 2: Khối tròn xoay được tạo bởi:

Đường thẳng y=f(x)
Đường thẳng y=g(x)
x=a ; x=b

Khi đó công thức tính thể tích khối tròn xoay sẽ là

$V=\pi \int_{a}^{b}\left[f^{2}(x)-g^{2}(x)\right] d x(g(x) \leq f(x) \text { với } \forall x \in[a ; b])$ $V=\pi \int_{a}^{b}\left[f^{2}(x)-g^{2}(x)\right] d x(g(x) \leq f(x) \text { với } \forall x \in[a ; b])$

3. Tính thể tích khối tròn xoay quanh trục Oy

Nếu khối tròn xoay quanh trục Oy thì để tính thể tích khối tròn xoay có thể áp dụng các công thức sau:

Trường hợp 1: Khối tròn xoay được tạo bởi:

Đường x=g(y)
Trục tung $(\mathrm{x}=0)$ $(\mathrm{x}=0)$
$\mathrm{y}=\mathrm{c} ; \mathrm{y}=\mathrm{d}$ $\mathrm{y}=\mathrm{c} ; \mathrm{y}=\mathrm{d}$

Khi đó công thức tính thể tích khối tròn xoay sẽ là:

$V=\pi \int_{c}^{d} g^{2}(y) d y$ $V=\pi \int_{c}^{d} g^{2}(y) d y$

Trường hợp 2 : Khối tròn xoay được tạo bởi:

Đường x=f(y)
Đường x=g(y)
$\mathrm{y}=\mathrm{c} ; \mathrm{y}=\mathrm{d}$ $\mathrm{y}=\mathrm{c} ; \mathrm{y}=\mathrm{d}$

Khi đó thể tích khối tròn xoay sẽ được tính theo công thức sau:

$V=\pi \int_{c}^{d}\left[f^{2}(y)-g^{2}(y)\right] d y \quad(g(y) \leq f(y) v \text { ới } \forall y \in[c ; d])$ $V=\pi \int_{c}^{d}\left[f^{2}(y)-g^{2}(y)\right] d y \quad(g(y) \leq f(y) v \text { ới } \forall y \in[c ; d])$

4. Ví dụ tích thể tích khối tròn xoay

Ví dụ 1: Cho khối tròn xoay được tạo bởi đường thẳng $y=\sqrt{x}$ $y=\sqrt{x}$ ; y=x và quay quanh trục Ox, hãy tính thể tích khối tròn xoay thu được.

Giải:

Giải phương trình: $\sqrt{x}=x \Leftrightarrow x \in\{0 ; 1\}$ $\sqrt{x}=x \Leftrightarrow x \in\{0 ; 1\}$

Thể tích khối tròn xoay là:

$V=\pi \int_{0}^{1} \int(\sqrt{x})^{2} d x-\pi \int_{0}^{1} \int(x)^{2} d x=\frac{\pi}{6}(d v t t)$ $V=\pi \int_{0}^{1} \int(\sqrt{x})^{2} d x-\pi \int_{0}^{1} \int(x)^{2} d x=\frac{\pi}{6}(d v t t)$

Ví dụ 2: Tính thể tích khối tròn xoay được tạo bởi các đường $y=\frac{2}{y}$ $y=\frac{2}{y}$; trục tung, $\mathrm{y}= 1 ; \mathrm{y}=4$ $\mathrm{y}= 1 ; \mathrm{y}=4$

Giải:

Thể tích khối tròn xoay được tạo bởi các đường $y=\frac{2}{y}$ $y=\frac{2}{y}$; trục tung, $\mathrm{y}= 1 ; \mathrm{y}=4$ $\mathrm{y}= 1 ; \mathrm{y}=4$ là

$V=\pi \int_{1}^{4}\left(\frac{2}{y}\right)^{2} d y=\int_{1}^{4} \frac{4}{y^{2}} d y=-\frac{4}{y} l_{1}^{4}=3(\mathrm{~d} v t t)$ $V=\pi \int_{1}^{4}\left(\frac{2}{y}\right)^{2} d y=\int_{1}^{4} \frac{4}{y^{2}} d y=-\frac{4}{y} l_{1}^{4}=3(\mathrm{~d} v t t)$

Ví dụ 3: Tính thể tích khối tròn xoay được tạo bởi $y=\sqrt{x} ; y=-x+2 ; y=0$ $y=\sqrt{x} ; y=-x+2 ; y=0$quanh quanh trục Oy

Giải

Ta viết lại các đường $\left\{\begin{array}{l}y \geq 0 \\ x=y^{2}\end{array}, x=2-y, y=0\right.$ $\left\{\begin{array}{l}y \geq 0 \\ x=y^{2}\end{array}, x=2-y, y=0\right.$

Khi đó thể tích khối tròn xoay được tính như sau

$V=\left|\pi \int_{0}^{1}(2-y)^{2}-\left(y^{2}\right)^{2} d y\right|=\frac{32 \pi}{15}(\mathrm{~d} v t t)$ $V=\left|\pi \int_{0}^{1}(2-y)^{2}-\left(y^{2}\right)^{2} d y\right|=\frac{32 \pi}{15}(\mathrm{~d} v t t)$

Ví dụ 4

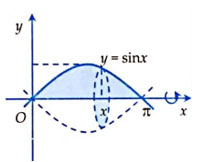
Tính thể tích của khối tròn xoay thu được khi quay hình phẳng được giới hạn bởi đường cong y = sinx, trục hoành và hai đường thẳng x=0, x=π (hình vẽ) quanh trục Ox.

Lời giải

Áp dụng công thức ở định lý trên ta có

$V=\pi \int_0^\pi \sin ^2 x d x=\frac{\pi}{2} \int_0^\pi(1-\cos 2 x) d x$ $V=\pi \int_0^\pi \sin ^2 x d x=\frac{\pi}{2} \int_0^\pi(1-\cos 2 x) d x$

$=\left.\frac{\pi}{2}\left(x-\frac{1}{2} \sin 2 x\right)\right|_0 ^\pi$ $=\left.\frac{\pi}{2}\left(x-\frac{1}{2} \sin 2 x\right)\right|_0 ^\pi$

$=\frac{\pi}{2}\left(\pi-\frac{1}{2} \sin 2 \pi\right)-\frac{\pi}{2}\left(0-\frac{1}{2} \sin 0\right)$ $=\frac{\pi}{2}\left(\pi-\frac{1}{2} \sin 2 \pi\right)-\frac{\pi}{2}\left(0-\frac{1}{2} \sin 0\right)$

$=\frac{\pi^2}{2}$ $=\frac{\pi^2}{2}$

Ví dụ 5

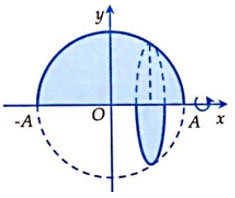
Tính thể tích khối tròn xoay thu được khi quay hình phẳng được giới hạn bởi đường cong $y=\sqrt{A^2-x^2}$ $y=\sqrt{A^2-x^2}$ và trục hoành quanh trục hoành.

Giải:

Ta thấy:

$y=\sqrt{A^2-x^2}<=>\ y^2=A^2\ -x^2\ \ <=>\ y^2\ +x^2\ =\ A^2$ $y=\sqrt{A^2-x^2}<=>\ y^2=A^2\ -x^2\ \ <=>\ y^2\ +x^2\ =\ A^2$

Do $\sqrt{A^2-x^2}\ge\ 0$ $\sqrt{A^2-x^2}\ge\ 0$ với mọi x, do vậy đây là phương trình nửa đường tròn tâm O, bán kính R = A nằm phía trên trục Ox. Khi quay quanh trục Ox thì hình phẳng sẽ tạo nên một khối cầu tâm O, bán kính R = A (hình vẽ). Do vậy ta có luôn

$V=\frac{4}{3}\pi A^3$ $V=\frac{4}{3}\pi A^3$

Vậy với bài toán dạng này, ta không cần viết công thức tích phân mà kết luận luôn theo công thức tính thể tích khối cầu.

Ví dụ 6

Tính thể tích của vật thể nằm giữa hai mặt phẳng x = 0 và x = 1, biết thiết diện của vật thể cắt bởi mặt phẳng (P) vuông góc với trục Ox tại điểm có hoành độ x(0≤x≤1) là một hình chữ nhật có độ dài hai cạnh là x và ln(x²+1).

Giải:

Do thiết diện là hình chữ nhật nên diện tích thiết diện là:

$S(x)=x\ln(x2^{ }+1)$ $S(x)=x\ln(x2^{ }+1)$

Ta có thể tích cần tính là

$\mathrm{V}=\int_0^1 \mathrm{x} \ln \left(\mathrm{x}^2+1\right) \mathrm{dx}$ $\mathrm{V}=\int_0^1 \mathrm{x} \ln \left(\mathrm{x}^2+1\right) \mathrm{dx}$

$\mathrm{V}=\frac{1}{2} \int_0^1 \ln \left(\mathrm{x}^2+1\right) \mathrm{d}\left(\mathrm{x}^2+1\right)$ $\mathrm{V}=\frac{1}{2} \int_0^1 \ln \left(\mathrm{x}^2+1\right) \mathrm{d}\left(\mathrm{x}^2+1\right)$

$=\left.\frac{1}{2}\left(\mathrm{x}^2+1\right) \ln \left(\mathrm{x}^2+1\right)\right|_0 ^1-\frac{1}{2} \int_0^1\left(\mathrm{x}^2+1\right) \mathrm{d}\left(\ln \left(\mathrm{x}^2+1\right)\right)$ $=\left.\frac{1}{2}\left(\mathrm{x}^2+1\right) \ln \left(\mathrm{x}^2+1\right)\right|_0 ^1-\frac{1}{2} \int_0^1\left(\mathrm{x}^2+1\right) \mathrm{d}\left(\ln \left(\mathrm{x}^2+1\right)\right)$

$=\ln 2-\frac{1}{2} \int_0^1 2 x d x=\ln 2-\frac{1}{2}$ $=\ln 2-\frac{1}{2} \int_0^1 2 x d x=\ln 2-\frac{1}{2}$

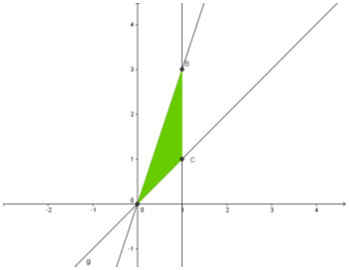
Ví dụ 7: Cho hình phẳng giới hạn bởi các đường y = 3x; y = x; x = 0; x = 1 quay xung quanh trục Ox. Tính thể tích của khối tròn xoay tạo thành.

Giải:

Tọa độ giao điểm của đường x = 1 với y = x và y = 3x là các điểm C(1;1) và B(3;1). Tọa độ giao điểm của đường y = 3x với y = x là O(0;0).

Vậy thể tích của khối tròn xoay cần tính là:

$V=\pi \int_0^1\left|9 x^2-x^2\right| d x=\pi \int_0^1 8 x^2 d x$ $V=\pi \int_0^1\left|9 x^2-x^2\right| d x=\pi \int_0^1 8 x^2 d x$

$\Leftrightarrow V=\left.\pi \frac{8 x^3}{3}\right|_0 ^1=\frac{8}{3} \pi$ $\Leftrightarrow V=\left.\pi \frac{8 x^3}{3}\right|_0 ^1=\frac{8}{3} \pi$

Ví dụ 8 Cho hình phẳng giới hạn bởi các đường y = 2x²; y² = 4x quay xung quanh trục Ox. Tính thể tích của khối tròn xoay tạo thành.

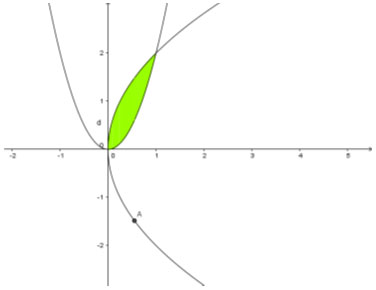
Giải:

Với $x\in[0;2]$ $x\in[0;2]$ thì $y^2=4x$ tương đương $y=2\sqrt{x}$ $y=2\sqrt{x}$. Tọa độ giao điểm của đường $\mathrm{y}=2 \mathrm{x}^2$ $\mathrm{y}=2 \mathrm{x}^2$ với $\mathrm{y}^2=4 \mathrm{x}$ $\mathrm{y}^2=4 \mathrm{x}$ là các điểm O(0;0) và A(1;2).

Vậy thể tích của khối tròn xoay cần tính là:

$V=\pi \int_0^1\left|4 x-4 x^4\right| d x=\pi \int_0^1\left(4 x-4 x^4\right) d x$ $V=\pi \int_0^1\left|4 x-4 x^4\right| d x=\pi \int_0^1\left(4 x-4 x^4\right) d x$

$V=\left.\pi \cdot\left(2 x^2-\frac{4 x^5}{5}\right)\right|_0 ^1=\frac{6}{5} \pi$ $V=\left.\pi \cdot\left(2 x^2-\frac{4 x^5}{5}\right)\right|_0 ^1=\frac{6}{5} \pi$

Tải về

Liên kết tải về

Công thức tính thể tích khối tròn xoay 392,8 KB

Tải về

Tìm thêm: Toán 12

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!