Bài tập sự đồng biến và nghịch biến của hàm số Chuyên đề sự đồng biến nghịch biến của hàm số
Bài tập sự đồng biến và nghịch biến của hàm số là nguồn tư liệu vô cùng hay, hữu ích dành cho các bạn học sinh lớp 12 ôn tập chuẩn bị thi THPT Quốc gia 2023.
Bài tập về đồng biến và nghịch biến của hàm số tổng hợp toàn bộ kiến thức lý thuyết, cách giải ví dụ minh họa kèm theo rất nhiều bài tập về đồng biến, nghịch biến có đáp án. Qua tài liệu này giúp học sinh có thể hiểu sâu được hướng suy luận, đồng thời có thể giải quyết được các bài toán tương tự. Ngoài ra các bạn xem thêm: phương pháp tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm nhiều biến, bộ công thức giải nhanh Toán 12, Công thức tính thể tích khối tròn xoay.
Bài tập sự đồng biến và nghịch biến của hàm số
A. Lý thuyết
1. Định nghĩa
+ Hàm số ![]() \(y=f\left( x \right)\) đồng biến trên khoảng
\(y=f\left( x \right)\) đồng biến trên khoảng ![]() \(\left( a,b \right)\) khi và chỉ khi
\(\left( a,b \right)\) khi và chỉ khi ![]() \(f'\left( x \right)\ge 0\) với mọi giá trị x thuộc khoảng
\(f'\left( x \right)\ge 0\) với mọi giá trị x thuộc khoảng ![]() \(\left( a,b \right)\). Dấu bằng xảy ra tại hữu hạn điểm.
\(\left( a,b \right)\). Dấu bằng xảy ra tại hữu hạn điểm.
+ Hàm số ![]() \(y=f\left( x \right)\) nghịch biến trên khoảng
\(y=f\left( x \right)\) nghịch biến trên khoảng ![]() \(\left( a,b \right)\) khi và chỉ khi
\(\left( a,b \right)\) khi và chỉ khi ![]() \(f'\left( x \right)\le 0\) với mọi giá trị x thuộc khoảng
\(f'\left( x \right)\le 0\) với mọi giá trị x thuộc khoảng ![]() \(\left( a,b \right)\). Dấu bằng xảy ra tại hữu hạn điểm.
\(\left( a,b \right)\). Dấu bằng xảy ra tại hữu hạn điểm.
2. Định lí
Cho hàm số y=f(x) có đạo hàm trên K.
a) Nếu ![]() \(f^{\prime}(x)>0\) với mọi x thuộc K thì hàm số f(x) đồng biến trên K.
\(f^{\prime}(x)>0\) với mọi x thuộc K thì hàm số f(x) đồng biến trên K.
b) Nếu ![]() \(f^{\prime}(x)<0\) với mọi x thuộc K thì hàm số f(x) nghịch biến trên K.
\(f^{\prime}(x)<0\) với mọi x thuộc K thì hàm số f(x) nghịch biến trên K.
c) Nếu ![]() \(f^{\prime}(x)=0\) với mọi x thuộc K thì hàm số f(x) không đổi trên K.
\(f^{\prime}(x)=0\) với mọi x thuộc K thì hàm số f(x) không đổi trên K.
Chú ý: Nếu hàm số f liên tục trên đoạn [a ; b] và có đạo hàm ![]() \(f^{\prime}(x)>0\) trên khoảng (a ; b) thì hàm số f đồng biến trên đoạn [a ; b]. Nếu hàm số f liên tục trên đoạn [a ; b] và có đạo hàm
\(f^{\prime}(x)>0\) trên khoảng (a ; b) thì hàm số f đồng biến trên đoạn [a ; b]. Nếu hàm số f liên tục trên đoạn [a ; b] và có đạo hàm ![]() \(f^{\prime}(x)<0\) trên khoảng (a ; b) thì hàm số f nghịch biến trên đoạn [a ; b].
\(f^{\prime}(x)<0\) trên khoảng (a ; b) thì hàm số f nghịch biến trên đoạn [a ; b].
3. Định lí mở rộng:
Cho hàm số y=f(x) có đạo hàm trên K.
a) Nếu ![]() \(f^{\prime}(x) \geq 0\) với mọi x thuộc K và
\(f^{\prime}(x) \geq 0\) với mọi x thuộc K và ![]() \(f^{\prime}(x)=0\) xảy ra tại một số hữu hạn điểm của K thì hàm số f(x) đồng biến trên K.
\(f^{\prime}(x)=0\) xảy ra tại một số hữu hạn điểm của K thì hàm số f(x) đồng biến trên K.
b) Nếu ![]() \(f^{\prime}(x) \leq 0\) với mọi x thuộc K và
\(f^{\prime}(x) \leq 0\) với mọi x thuộc K và ![]() \(f^{\prime}(x)=0\) xảy ra tại một số hữu hạn điểm của K thì hàm số f(x) nghịch biến trên K.
\(f^{\prime}(x)=0\) xảy ra tại một số hữu hạn điểm của K thì hàm số f(x) nghịch biến trên K.
4. Quy tắc xét tính đơn điệu của hàm số
Bước 1: Tìm tập xác định.
Bước 2: Tính đạo hàm ![]() \(f^{\prime}(x)\). Tìm các điểm
\(f^{\prime}(x)\). Tìm các điểm ![]() \(x_{i}(i=1,2, \ldots, n)\) mà tại đó đạo hàm bằng 0 hoặc không xác định.
\(x_{i}(i=1,2, \ldots, n)\) mà tại đó đạo hàm bằng 0 hoặc không xác định.
Bước 3: Sắp xếp các điểm ![]() \(x_{i}\) theo thứ tự tăng dần và lập bảng biến thiên.
\(x_{i}\) theo thứ tự tăng dần và lập bảng biến thiên.
Bước 4: Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.
5. Ví dụ minh họa
Vi dụ 1: Xét tính đơn điệu của mỗi hàm số sau:
a. ![]() \(y=x^{3}-3 x^{2}+2\)
\(y=x^{3}-3 x^{2}+2\)
b. ![]() \(y=-x^{3}+3 x^{2}-3 x+2\)
\(y=-x^{3}+3 x^{2}-3 x+2\)
c![]() \(. y=x^{3}+2 x\)
\(. y=x^{3}+2 x\)
Hướng dẫn giải
a. ![]() \(y=x^{3}-3 x^{2}+2\)
\(y=x^{3}-3 x^{2}+2\)
- Hàm số xác định với mọi ![]() \(x \in \mathbb{R}.\)
\(x \in \mathbb{R}.\)
- Ta có: ![]() \(y^{\prime}=3 x^{2}-6 x\), cho
\(y^{\prime}=3 x^{2}-6 x\), cho ![]() \(y^{\prime}=0 \Rightarrow 3 x^{2}-6 x=0 \Leftrightarrow x=0, x=2.\)
\(y^{\prime}=0 \Rightarrow 3 x^{2}-6 x=0 \Leftrightarrow x=0, x=2.\)
- Bảng biến thiên:
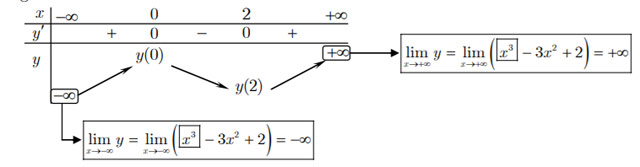
- Dựa vào bảng biến thiên suy ra:
' Hàm số đồng biến trên các khoảng ![]() \((-\infty ; 0) và (2 ;+\infty).\)
\((-\infty ; 0) và (2 ;+\infty).\)
ㄴ Hàm số nghịch biến trên khoảng (0 ; 2).
Chú![]() \(\dot{y}\) : Không được kết luận: "Hàm số đồng biến trên khoảng
\(\dot{y}\) : Không được kết luận: "Hàm số đồng biến trên khoảng ![]() \((-\infty ; 0) \cup(2 ;+\infty)\)"
\((-\infty ; 0) \cup(2 ;+\infty)\)"
![]() \(b. y=-x^{3}+3 x^{2}-3 x+2\)
\(b. y=-x^{3}+3 x^{2}-3 x+2\)
- Hàm số xác định với mọi ![]() \(x \in \mathbb{R}.\)
\(x \in \mathbb{R}.\)
- Ta có: ![]() \(y^{\prime}=-3 x^{2}+6 x-3\), cho
\(y^{\prime}=-3 x^{2}+6 x-3\), cho ![]() \(y^{\prime}=0 \Rightarrow-3 x^{2}+6 x-3=0 \Rightarrow x=1\) (nghiệm kép)
\(y^{\prime}=0 \Rightarrow-3 x^{2}+6 x-3=0 \Rightarrow x=1\) (nghiệm kép) ![]() \(\Rightarrow y^{\prime} \leq 0, \forall x \in \mathbb{R} \Rightarrow\) hàm số luôn nghịch biến trên tập xác định
\(\Rightarrow y^{\prime} \leq 0, \forall x \in \mathbb{R} \Rightarrow\) hàm số luôn nghịch biến trên tập xác định ![]() \(\mathbb{R}.\)
\(\mathbb{R}.\)
![]() \(c. y=x^{3}+2 x.\)
\(c. y=x^{3}+2 x.\)
- Hàm số xác định với mọi ![]() \(x \in \mathbb{R}.\)
\(x \in \mathbb{R}.\)
- ![]() \(y^{\prime}=3 x^{2}+2, cho y^{\prime}=0 \Rightarrow 3 x^{2}+2=0\) (vô nghiệm)
\(y^{\prime}=3 x^{2}+2, cho y^{\prime}=0 \Rightarrow 3 x^{2}+2=0\) (vô nghiệm)![]() \(\Rightarrow y^{\prime}>0, \forall x \in \mathbb{R} \Rightarrow\) hàm số luôn đồng biến trên tập xác định R
\(\Rightarrow y^{\prime}>0, \forall x \in \mathbb{R} \Rightarrow\) hàm số luôn đồng biến trên tập xác định R
..................
Tải File tài liệu để xem thêm nội dung chi tiết tài liệu
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:












 Đề thi học kì 1 Lớp 12
Đề thi học kì 1 Lớp 12
 Đề thi giữa học kì 1 Lớp 12
Đề thi giữa học kì 1 Lớp 12
 Đề thi giữa học kì 2 Lớp 12
Đề thi giữa học kì 2 Lớp 12
 Đề thi học kì 2 Lớp 12
Đề thi học kì 2 Lớp 12
 Soạn Văn 12 KNTT
Soạn Văn 12 KNTT
 Soạn Văn 12 CTST
Soạn Văn 12 CTST
 Soạn Văn 12 Cánh Diều
Soạn Văn 12 Cánh Diều
 Văn 12
Văn 12
 Toán 12 Chân trời sáng tạo
Toán 12 Chân trời sáng tạo









