Thể tích khối lăng trụ: Công thức và bài tập Công thức tính thể tích khối lăng trụ

Khối lăng trụ là gì? Công thức tính khối lăng trụ như thế nào? Đây là câu hỏi được rất nhiều bạn học sinh quan tâm? Vì thế hãy cùng Eballsviet.com theo dõi bài viết dưới đây.

Trong bài học hôm nay chúng tôi sẽ giới thiệu đến các bạn học sinh toàn bộ kiến thức về hình lăng trụ, cách tính thể tích khối lăng trụ kèm theo một số dạng bài tập có đáp án giải chi tiết kèm theo. Hi vọng đây sẽ là nguồn tư liệu hữu ích, giúp các em củng cố kỹ năng giải toán để đạt được kết quả cao trong các bài kiểm tra, bài thi sắp tới. Ngoài ra các bạn xem thêm công thức tính chu vi hình chữ nhật, công thức tính diện tích hình vuông.

Thể tích khối lăng trụ: Công thức và bài tập

1. Hình lăng trụ là gì?

Một đa giác có hai mặt đáy song song và bằng nhau, mặt bên là hình bình hành thì đa giác đó gọi là hình lăng trụ.

Tên gọi hình lăng trụ

Tên của hình lăng trụ người ta đặt tên theo mặt đáy.

Ví dụ:

- Mặt đáy hình tam giác đều thì gọi là hình lăng trụ tam giác đều.

- Mặt đáy hình tứ giác đều thì gọi là hình lăng trụ tứ giác đều.

Hình lăng trụ đứng

Nếu như hình lăng trụ mà có các cạnh bên vuông góc với mặt đáy thì người ta gọi là hình lăng trụ đứng.

Lưu ý:

- Nếu mặt đáy là hình chữ nhật thì hình trụ đứng của tứ giác có tên gọi khác là hình hộp chữ nhật.

- Nếu hình trụ đứng tứ giác có 12 cạnh đều có độ dài là a thì tên gọi của nó là hình lập phương.

2. Một số dạng lăng trụ

a) Hình lăng trụ đứng: là hình lăng trụ có cạnh bên vuông góc với đáy. Độ dài cạnh bên được gọi là chiều cao của hình lăng trụ. Lúc đó các mặt bên của hình lăng trụ đứng là các hình chữ nhật

b) Hình lăng trụ đều: là hình lăng trụ đứng có đáy là đa giác đều. Các mặt bên của lăng trụ đều là các hình chữ nhật bằng nhau. Ví dụ: hình lăng trụ tam giác đều, tứ giác đều... thì ta hiểu là hình lăng trụ đều

c) Hình hộp: Là hình lăng trụ có đáy là hình bình hành

d) Hình hộp đứng: là hình lăng trụ đứng có đáy là hình bình hành

e) Hình hộp chữ nhật: là hình hộp đứng có đáy là hình chữ nhật

f) Hình lăng trụ đứng có đáy là hình vuông và các mặt bên đều là hình vuông được gọi là hình lập phương (hay hình chữ nhật có ba kích thước bằng nhau được gọi là hình lập phương)

Nhận xét:

• Hình hộp chữ nhật là hình lăng trụ đứng (Có tất cả các mặt là hình chữ nhật
• Hình lập phương là hình lăng trụ đều (tất cả các cạnh bằng nhau)
• Hình hộp đứng là hình lăng trụ đứng (mặt bên là hình chữ nhật, mặt đáy là hình bình hành)

3. Thể tích khối lăng trụ đứng

Công thức tính thể tích hình lăng trụ đứng:

V=S.h

Trong đó:

• S là diện tích đáy
• h là chiều cao của khối lăng trụ.

Chú ý: Lăng trụ đều là hình lăng trụ đứng có đáy là đa giác đều.

4. Ví dụ tính thể tích khối lăng trụ

Ví dụ 1:

Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh bằng a = 2 cm và chiều cao là h = 3 cm. Hãy tính thể tích hình lăng trụ này?

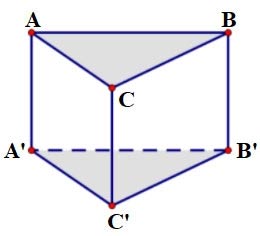
Giải:

Vì đáy là tam giác đều cạnh a nên diện tích: \(S_{A B C}=a^2 \cdot \frac{\sqrt{3}}{4}=2^2 \cdot \frac{\sqrt{3}}{4}=\sqrt{3}\left(m^2\right)\)

Khi này, thể tích hình lăng trụ là:

\(V=S_{A B C} \cdot h=\sqrt{3} \cdot 3=3 \sqrt{3}\left(m^3\right)\)

Ví dụ 2:

Cho hình hộp đứng có các cạnh AB = 3a, AD = 2a, AA’= 2a. Tính thể tích của khối A’.ACD’

Hướng dẫn:

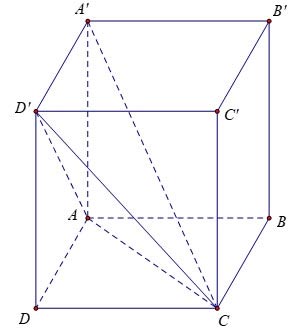
Do mặt bên ADD’A’ là hình chữ nhật nên ta có:

\(S_{A A^{\prime} D^{\prime}}=\frac{1}{2} S_{A A^{\prime} D^{\prime} D}\)

\(V_{A^{\prime} \cdot A C D^{\prime}}=V_{C \cdot A A^{\prime} D^{\prime}}=\frac{1}{2} V_{C \cdot A A^{\prime} D^{\prime} D}\)

\(=\frac{1}{2} \cdot \frac{1}{3} V_{A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}}\)

\(=\frac{1}{6} \cdot 3 a \cdot 2 a \cdot 2 a=2 a^3\)

Ví dụ 3: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh a√3, góc giữa và đáy là 60º. Gọi M là trung điểm của BB'. Tính thể tích của khối chóp M.A’B’C’.

Giải:

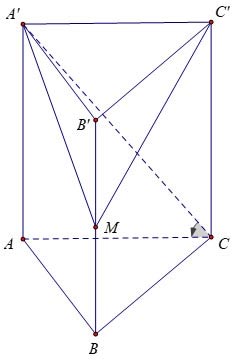
Do \(A A^{\prime} \perp(A B C)\) nên suy ra

\(\left(\mathrm{A}^{\prime} \mathrm{C},(\mathrm{ABC})\right)=\widehat{A^{\prime} C A}=60^{\circ}\)

Ta có: \(A A^{\prime}=A C \cdot \tan \widehat{A^{\prime} C A}\) \(=a \sqrt{3} \cdot \tan 60^{\circ}=3 a\)

\(S_{A^{\prime B}{ }^{\prime \prime} C^{\prime}}=\frac{(a \sqrt{3})^2 \sqrt{3}}{4}=\frac{3 a^2 \sqrt{3}}{4}\)

\(M B^{\prime}=\frac{A A^{\prime}}{2}=\frac{3 a}{2}\)

\(\Rightarrow V_{M \cdot A^{\prime} B^{\prime} C^{\prime}}=\frac{1}{3} M B^{\prime} \cdot S_{A^{\prime} B^{\prime} C^{\prime}}=\frac{3 a^2 \sqrt{3}}{8}\)

Ví dụ 4:

Cho lăng trụ tứ giác đều ABCD.A’B’C’D’ có cạnh đáy bằng a và mặt (DBC’) với đáy ABCD một góc 60º. Tính thể tích khối lăng trụ ABCD.A’B’C’D?

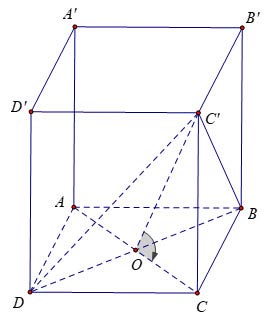
Ta có: \(AC ⊥ BD\) tại tâm O của hình vuông ABCD.

Mặt khác \(CC' ⊥ BD\) do đó \(BD ⊥ (COC')\)

Suy ra \(((C'BD),(ABCD)) = ∠(C'OD) = 60º\)

Lại có:

\(O C=\frac{A C}{2}=\frac{a \sqrt{2}}{2}\)

\(\Rightarrow C C^{\prime}=O C \cdot \tan \widehat{C^{\prime} O D}\) \(=\frac{a \sqrt{2}}{2} \cdot \tan 60^{\circ}=\frac{a \sqrt{6}}{2}\)

\(V_{A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}}=S_{A B C D} \cdot C C^{\prime}\)

\(=a^2 \cdot \frac{a \sqrt{6}}{2}=\frac{a^3 \sqrt{6}}{2}\)

5. Bài tập thể tích khối lăng trụ 

Bài 1. Một bể nước hình trụ có diện tích mặt đáy B = 2 m² và đường cao h = 1 m. Thể tích của bể nước này bằng bao nhiêu?

Lời giải

Áp dụng công thức V = B.h = 2.1 = 2 m³.

Bài 2: Cho hình lăng trụ đứng \(ABC \cdot A^{\prime} B^{\prime} C^{\prime}\) có đáy là tam giác vuông tại B, \(\mathrm{AB}=\mathrm{a}, \mathrm{BC}=2 \mathrm{a}, \mathrm{AA}^{\prime}=3 \mathrm{a}\). Mặt phẳng \((\alpha)\)qua A vuông góc với \(\mathrm{CA}^{\prime}\) lần lượt cắt các đoạn thẳng \(\mathrm{CC}^{\prime}\) và \(\mathrm{BB}^{\prime}\) tại M và N. Diện tích tam giác \(\mathrm{AMN}\) là

\(A. \frac{a^{2} \sqrt{14}}{6}\)

\(B. \frac{a^{2} \sqrt{14}}{3}\)

\(C. \frac{a^{2} \sqrt{14}}{9}\)

\(D. \frac{a^{2} \sqrt{14}}{7}\)

Câu 3: Cho hình lăng trụ tứ giác đều có tất cả các cạnh bằng a. Thể tích khối lăng trụ này:

\(A. \frac{{{a}^{3}}}{2}\)	\(B. {{a}^{3}}\)
\(C. \frac{{{a}^{3}}}{3}\)	\(D. \frac{\sqrt{3}{{a}^{3}}}{4}\)

Câu 4 Cho lăng trụ tứ giác đều ABCD.A’B’C’D’ có cạnh bên bằng 4a và đường chéo 5a. Tính thể tích của khối lăng trụ này là:

\(A. 9{{a}^{3}}\)	\(C. 3{{a}^{3}}\)
\(B. 12{{a}^{3}}\)	\(D. 18{{a}^{3}}\)

Câu 5: Cho lăng trụ đứng ABC. A’B’C’ có đáy ABC là tam giác vuông tại B. AB = 2a, BC = a, \(AA'=2a\sqrt{3}\). Tính theo a thể tích khối lăng trụ ABC.A’B’C’.

\(A. \frac{2{{a}^{3}}\sqrt{3}}{3}\)	\(B. \frac{{{a}^{3}}\sqrt{3}}{3}\)
\(C. 2{{a}^{3}}\sqrt{3}\)	\(D. 4{{a}^{3}}\sqrt{3}\)

Câu 6: Cho hình lăng trụ tam giác đều có cạnh đáy bằng a, diện tích một mặt bên là \(2{{a}^{2}}\). Thể tích của khối lăng trụ đó là:

\(A. \frac{{{a}^{3}}\sqrt{3}}{2}\)	\(B. \frac{{{a}^{3}}\sqrt{3}}{3}\)
\(C. {{a}^{3}}\sqrt{3}\)	\(D. \frac{\sqrt{3}{{a}^{3}}}{6}\)

Câu 7 Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, AD = _{\(a\sqrt{2}\)}, SA = a, SA vuông góc với mặt phẳng đáy. Gọi M, N lần lượt là trung điểm của AD và SC, I là giao điểm của BM và AC. Thể tích khối tứ diện ANIB tính theo a là:

\(A. \frac{{{a}^{3}}\sqrt{2}}{72}\)	\(B. \frac{{{a}^{3}}\sqrt{2}}{32}\)
\(C. \frac{{{a}^{3}}\sqrt{2}}{24}\)	\(D. \frac{{{a}^{3}}\sqrt{2}}{36}\)

Ngoài ra để vận dụng tốt công thức tính thể tính khối lăng trụ, các bạn xem thêm bài tập thể tích khối lăng trụ nhé.