Cách tính số đường chéo của đa giác Đường chéo của đa giác

Tải về

Cách tính số đường chéo của đa giác dưới đây là những công thức quan trọng giúp các em lớp 12 cần ghi nhớ để vận dụng tính toán nhanh nhất các bài toán liên quan đến đường chéo của đa giác và cho ra kết quả chính xác.

Trong kì thi THPT Quốc gia môn Toán thì số lượng công thức cần ghi nhớ là không hề nhỏ. Đối với các bài thi trắc nghiệm, điều cần thiết là các em học sinh cần nắm kiến thức rộng và có phương pháp giải nhanh hiệu quả để có thể ghi điểm nhiều nhất. Bên cạnh cách tính đường chéo của đa giác các bạn xem thêm bộ đề ôn thi THPT Quốc gia môn Toán, phân dạng câu hỏi và bài tập trong đề thi THPT Quốc gia môn Toán.

Cách tính số đường chéo của đa giác

1. Đa giác

Khi áp dụng vào đa giác, đường chéo là một đoạn thẳng nối hai đỉnh bất kỳ không liền kề. Do vậy, một tứ giác có hai đường chéo, nối hai cặp đỉnh đối diện nhau. Đối với bất kỳ đa giác lồi nào, tất cả các đường chéo đều nằm trong đa giác, nhưng đối với đa giác lõm, một số đường chéo nằm ngoài đa giác.

Bất kì đa giác nào với n - cạnh (n≥ 3), lồi hoặc lõm có $\frac{n\ \left(n-3\right)}{2}$ $\frac{n\ \left(n-3\right)}{2}$ đường chéo, vì mỗi đỉnh có đường chéo tới tất cả các đỉnh khác trừ bản thân nó và hai đỉnh liền kề, hoặc n - 3 đường chéo, và mỗi đường chéo được hai đỉnh chia sẻ.

2. Cách tính số đường chéo của đa giác?

Phương pháp giải

+) Số đường chéo của đa giác lồi n đỉnh là

$\frac{n\ \left(n-3\right)}{2}$ $\frac{n\ \left(n-3\right)}{2}$

+) Để tìm số cạnh của đa giác khi biết số đường chéo, ta dùng công thức trên.

3. Số miền do đường chéo tạo ra

Trong một đa giác lồi, nếu không có ba đường chéo đồng quy nào, thì số vùng mà các đường chéo chia bên trong đa giác là

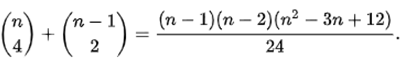
Với n=3. 4,... số vùng tạo ra là

1, 4, 11, 25, 50, 91, 154, 246...

Đây là chuỗi OEIS A006522.

4. Ví dụ tính số đường chéo đa giác

Câu 1: Cho đa giác 8 cạnh, số đường chéo của đa giác đó là:

A. 40
B. 28
C. 20
D. 16

Lời giải:

Số đường chéo của đa giác lồi n cạnh là:

áp dụng công thức: $\frac{n\ \left(n-3\right)}{2} = \frac{8\ \left(8-3\right)}{2} = 20$ $\frac{n\ \left(n-3\right)}{2} = \frac{8\ \left(8-3\right)}{2} = 20$

Câu 2: Một đa giác 7 cạnh thì số đường chéo của đa giác đó là ?

A. 12.
B. 13.
C. 14.
D. Kết quả khác.

Lời giải:

Số đường chéo của đa giác n cạnh là $\frac{n\ \left(n-3\right)}{2}$ $\frac{n\ \left(n-3\right)}{2}$

Khi đó số đường chéo của đa giác 7 cạnh là $\frac{7\ \left(7-3\right)}{2} = 14$ $\frac{7\ \left(7-3\right)}{2} = 14$ (đường chéo)

Câu 3 Số đường chéo xuất phát từ 1 đỉnh của đa giác 20 cạnh là?

A. 15
B. 16
C. 17
D. 18

Lời giải:

Số đường chéo xuất phát từ 1 đỉnh của đa giác n cạnh là n – 3

Do đó, Số đường chéo xuất phát từ 1 đỉnh của đa giác 20 cạnh là: 20 – 3 = 17

Câu 4: Số đường chéo của đa giác 10 cạnh?

A. 50
B. 60
C. 70
D. 80