Đường cao trong tam giác cân Ôn tập Toán 8

Đường cao trong tam giác cân là một trong những kiến thức cơ bản trong chương trình Toán lớp 8, lớp 9 và thường xuất hiện trong các bài thi vào lớp 10.

Đường cao trong tam giác cân là đoạn thẳng kẻ từ đỉnh của tam giác xuống cạnh đáy và vuông góc với cạnh đáy đó. Trong tam giác cân, đường cao cũng đồng thời là đường trung tuyến và đường phân giác của góc tại đỉnh, chia tam giác thành hai tam giác vuông bằng nhau. Vậy sau đây là toàn bộ kiến thức về cách tính đường cao trong tam giác cân mời các bạn cùng theo dõi nhé. Bên cạnh đó các bạn xem thêm công thức tính đường cao trong tam giác.

1. Đường cao trong tam giác là gì?

Đoạn vuông góc kẻ từ 1 đỉnh đến đường thẳng chứa cạnh đối diện gọi là đường cao của tam giác đó. Mỗi tam giác có 3 đường cao

Ba đường cao của tam giác đi qua một điểm, điểm đó gọi là trực tâm của tam giác

2. Tính chất đường cao trong tam giác cân

Trong tam giác cân, đường cao có những tính chất đặc biệt như sau:

1. Đường cao trong tam giác cân cắt nhau tại một điểm duy nhất là giao điểm của các đường cao. Điều này có nghĩa là trong tam giác cân, các đường cao đồng dạng và đồng quy, tạo thành một điểm gọi là trung điểm Schiffler.

2. Đường cao trong tam giác cân chia tam giác thành hai tam giác vuông cân với các cạnh đáy tương ứng có độ dài bằng nhau. Điều này có nghĩa là đường cao là đường trung tuyến cũng như là đường phân giác của các tam giác vuông cân này.

3. Đường cao trong tam giác cân cũng là trung tuyến của tam giác gốc, chia tam giác thành hai nửa có diện tích bằng nhau.

4. Một tính chất đặc biệt khác là đường cao trong tam giác cân cũng là đường đối xứng của đường phân giác đi qua đỉnh tam giác. Điều này có nghĩa là đường cao trong tam giác cân có thể được coi là một trục bảo toàn năng lượng và góc quay.

Tóm lại, đường cao trong tam giác cân không chỉ đáng chú ý vì thành phần kỳ diệu của nó, mà còn vì những tính chất đặc biệt và liên quan của nó với các yếu tố khác trong tam giác.

3. Công thức tính đường cao trong tam giác cân

Giả sử các bạn có tam giác ABC cân tại A, đường cao AH vuông góc tại H như sau:

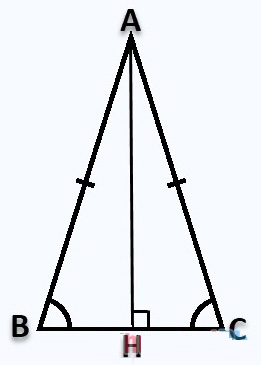
Công thức tính đường cao AH:

Vì tam giác ABC cân tại A nên đường cao AH đồng thời là đường trung tuyến nên:

\(\Rightarrow HB = HC = \frac{{BC}}{2}\)

Áp dụng định lý Pytago trong tam giác vuông ABH vuông tại H ta có:

\(A{H^2} + B{H^2} = A{B^2}\)

\(\Rightarrow A{H^2} = A{B^2} - B{H^2}\)

4. Tương quan giữa đường cao và cạnh đáy trong tam giác cân là gì?

Trong tam giác cân, đường cao và cạnh đáy có một mối quan hệ đặc biệt. Đường cao trong tam giác cân là một đường thẳng từ đỉnh của tam giác đến đường thẳng chứa cạnh đáy, vuông góc với cạnh đáy.

Mối quan hệ này có thể được mô tả như sau:

1. Đường cao trong tam giác cân cắt cạnh đáy tại trung điểm. Điều này có nghĩa là đường cao chia cạnh đáy thành hai phần có cùng độ dài.

2. Đường cao trong tam giác cân cũng là đường trung tuyến của tam giác. Điều này có nghĩa là đường cao chia tam giác thành hai nửa có diện tích bằng nhau.

3. Đường cao và cạnh đáy trong tam giác cân tạo thành một hình vuông khi kết hợp với cạnh đáy và hai cạnh còn lại của tam giác.

Với các tính chất đặc biệt này, đường cao và cạnh đáy trong tam giác cân tạo ra một sự cân đối đẹp và quan trọng trong tam giác.

5. Ví dụ tính đường cao trong tam giác cân

Ví dụ: Cho tam giác ABC cân tại A, đường cao AH vuông góc tại H như sau. Tính đường cao AH.

Hướng dẫn

Vì tam giác ABC cân tại A, đường cao AH đồng thời là đường trung tuyến nên:

Áp dụng định lý Pythagore trong tam giác vuông ABH vuông tại H ta có:

AH² + BH² = AB²

=> AH² = AB² − BH²

6. Bài tập đường cao trong tam giác cân

Câu 1: Cho tam giác MNP, 2 đường cao MH và ME cắt nhau tại G. Chọn đáp án đúng:

A. G là trọng tâm của tam giác MNP.
B. G là tâm đường tròn nội tiếp tam giác MNP.
C. PG là đường cao của tam giác MNP.
D. PG là đường trung trực của tam giác MNP.

Câu 2: Cho tam giác MNP cân tại M biết MH là đường trung tuyến khi đó:

A. MHNP vuông góc.
B. MH là đường trung trực của NP.
C. MH là đường phân giác của góc NMP.
D. A, B, C đều đúng.

Câu 3: Cho 2 đường thẳng xx’ và yy’ cách nhau tạo G. Trên Gx, Gx’ lần lượt lấy các điểm B, D sao cho GA = GB, GC = GD. Gọi M, N lần lượt là trung điểm của cạnh AB và CD. Chứng minh M, G, N thẳng hàng.

Câu 4: Cho tam giác ABC vuông tại A, có đường cao AH, biết AB : AC = 3; AB + AC = 21cm.

1. Tính độ dài các cạnh của tam giác ABC.

2. Tính đường cao AH.

7. Ứng dụng của đường cao trong giải toán và thực tế

Đường cao trong tam giác cân không chỉ quan trọng trong lĩnh vực hình học mà còn có nhiều ứng dụng thực tế. Dưới đây là một số ứng dụng nổi bật:

• Trong giáo dục: Đường cao là một công cụ cơ bản được sử dụng để dạy và học về các tính chất của tam giác, giúp học sinh hiểu sâu hơn về cấu trúc hình học.
• Trong kiến trúc: Các kiến trúc sư sử dụng kiến thức về đường cao để thiết kế mái nhà và các cấu trúc khác, đảm bảo tính cân bằng và ổn định của công trình.
• Trong kỹ thuật: Đường cao giúp các kỹ sư xác định trọng tâm của các cấu trúc, từ đó tính toán sức chịu tải và phân bổ lực một cách chính xác.

Bên cạnh đó, việc hiểu biết về đường cao còn có ích trong việc giải các bài toán liên quan đến diện tích và thể tích, đặc biệt trong các dự án xây dựng và thiết kế mô hình.

Ví dụ cụ thể:

Trong thiết kế mái nhà: Sử dụng đường cao để tính toán độ dốc mái nhà, đảm bảo mái nhà có độ dốc phù hợp để thoát nước mưa hiệu quả.

Trong phân tích cấu trúc: Kỹ sư sử dụng đường cao để xác định các điểm chịu lực trong cầu và các công trình khác, giúp tối ưu hóa thiết kế và đảm bảo an toàn.