Tam giác vuông cân Tính chất tam giác vuông cân
Tam giác vuông cân bao gồm tóm tắt lý thuyết kèm theo nhiều dạng câu hỏi khác nhau có đáp án giải chi tiết kèm theo bài tự luyện. Qua đó các bạn học sinh củng cố và mở rộng kiến thức giải toán về tam giác vuông cân.
Tính chất tam giác vuông cân là một trong những dạng bài tập quan trọng nằm trong chương trình SGK Toán 9. Chính vì thế qua tài liệu mà Eballsviet.com đăng tải dưới đây sẽ giúp các em tự tin kiểm tra và nắm vững kiến thức mình đã học về tính chất cách giải bài tập tam giác vuông cân. Vậy sau đây là trọn bộ kiến thức về tam giác vuông cân mời các bạn cùng theo dõi tại đây. Ngoài ra để nâng cao kiến thức môn Toán thật tốt các em xem thêm một số tài liệu như: chứng minh phương trình luôn có nghiệm với mọi m, chuyên đề Giải phương trình bậc 2 chứa tham số, bài tập hệ thức Vi-et và các ứng dụng.
Tam giác vuông cân
1. Tam giác vuông cân là gì
- Tam giác vuông cân vừa là tam giác vuông, vừa là tam giác cân hay nói cách khác tam giác vuông là tam giác có 2 cạnh vuông góc và bằng nhau.
– Tam giác ABC có AB = AC, AB ⊥ AC thì tam giác ABC vuông cân tại A.
2. Tính chất tam giác vuông cân
Tam giác vuông cân đồng thời là một tam giác vuông và cũng là tam giác cân. Ở tam giác vuông cân sẽ có hai góc nhọn, 1 góc vuông và có hai cạnh góc vuông bằng nhau. Mỗi góc nhọn trong tam giác vuông cân có độ lớn là 45 độ.
Với định nghĩa trên, tam giác vuông cân có những tính chất sau đây:
- Tam giác vuông cân sẽ có 2 góc đáy bằng nhau, đều bằng 45 độ.
- Tam giác vuông có 3 đường là đường cao, đường phân giác tính từ đỉnh góc vuông và đường trung tuyến sẽ trùng với nhau và 2 đường thẳng này sẽ có độ dài bằng nửa cạnh huyền.
3. Đường cao tam giác vuông cân
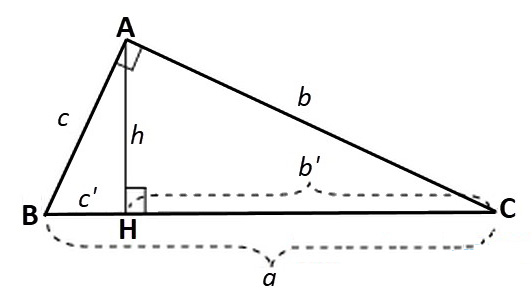
Công thức tính cạnh và đường cao trong tam giác vuông cân
![]() \(1.\ {a^2} = {b^2} + {c^2}\)
\(1.\ {a^2} = {b^2} + {c^2}\)
![]() \(2.\ {b^2} = a.b' và {c^2} = a.c'\)
\(2.\ {b^2} = a.b' và {c^2} = a.c'\)
![]() \(3.\ ah = bc\)
\(3.\ ah = bc\)
![]() \(4.\ {h^2} = b'.c'\)
\(4.\ {h^2} = b'.c'\)
![]() \(5.\ \frac{1}{{{h^2}}} = \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}\)
\(5.\ \frac{1}{{{h^2}}} = \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}\)
Trong đó: a, b, c lần lượt là các cạnh của tam giác vuông như hình trên;
b’ là đường chiếu của cạnh b trên cạnh huyền; c’ là đường chiếu của cạnh c trên cạnh huyền;
h là chiều cao của tam giác vuông được kẻ từ đỉnh góc vuông A xuống cạnh huyền BC.
Như vậy các bạn có thể dựa vào các công thức cạnh và đường cao trong tam giác vuông ở trên để giải quyết các bài toán.
Công thức tính cạnh huyền tam giác vuông cân
Theo định lý pitago, công thức tính cạnh huyền tam giác vuông cân bằng căn bậc hai của bình phương hai cạnh còn lại
![]() \(c\ =\sqrt{a^2+\ b^2}\)
\(c\ =\sqrt{a^2+\ b^2}\)
Trong đó:
c là cạnh huyền của tam giác vuông cân
a, b lần lượt là 2 cạnh còn lại
Như vậy các bạn có thể dựa vào các công thức cạnh và đường cao trong tam giác vuông ở trên để giải quyết các bài toán
4. Tính diện tích tam giác vuông cân
Tam giác ABC vuông cân tại A, a là độ dài hai cạnh góc vuông:
Áp dụng công thức tính diện tích tam giác vuông cho diện tích tam giác vuông cân với chiều cao và cạnh đáy bằng nhau, ta có công thức:
![]() \(S_{ABC}=\frac{1}{2}a^{2}\)
\(S_{ABC}=\frac{1}{2}a^{2}\)
5. Cách chứng minh tam giác vuông cân
Từ định nghĩa về tam giác vuông cân ta có các cách chứng minh tam giác vuông cân như sau:

- Tam giác có 1 góc vuông và 2 cạnh góc vuông bằng nhau là tam giác vuông cân
- Tam giác vuông có 1 góc nhọn bằng 45 độ
- Tam giác có 2 cạnh bằng nhau và 1 góc đáy bằng 45 độ
6. Ví dụ tam giác vuông cân
Ví dụ 1: Vẽ tam giác ABC vuông cân tại A.
Giải:
- Vẽ góc vuông xAy
- Trên tia Ax lấy điểm B, trên tia Ay lấy điểm C sao cho AB = AC
- Nối B với C
- Khi đó ta được tam giác ABC vuông cân tại A.
Ví dụ 2: Chọn đáp án đúng cho câu hỏi dưới đây
Tam giác ABC có hai góc B và góc C = 45o, Vậy tam giác ABC là tam giác gì?
A. Tam giác cân
B. Tam giác vuông
C. Tam giác đều
D. Tam giác vuông cân
Đáp án đúng: D- ABC là tam giác vuông cân
Giải thích:
Tam giác có hai góc B và C bằng 45o, tức là góc B = góc C = 45o.
Vì tổng ba góc trong một tam giác là 180o, ta có: A + B + C = 180o.
Thay vào giá trị góc B = C = 45o, ta có: A + 45o + 45o = 180o.
Từ đó, ta tính được góc A là: A = 180o - 45o - 45o = 90o.
Vậy tam giác ABC có một góc bằng 90o (góc A = 90o) và hai góc bằng nhau (góc B = góc C = 45o), nên đây là tam giác vuông cân.
Ví dụ 3:
Cho tam giác vuông cân ABC tại A, tia phân giác của các góc B và C cắt AC và AB lần lượt tại E và D
a, Chứng minh rằng BE = CD, AD = AE
b, Gọi I là giao điểm của BE và CD, AI cắt BC tại M. Chứng minh rằng các tam giác MAB và MAC là tam giác vuông cân
Gợi ý đáp án
a, Vì tam giác ABC cân tại A nên AB = AC và ![]() \(\widehat B = \widehat C\)
\(\widehat B = \widehat C\)
Vì BE là tia phân giác của góc B nên ![]() \(\widehat {ABE} = \widehat {EBC}\)
\(\widehat {ABE} = \widehat {EBC}\)
Và CD là tia phân giác của góc C nên ![]() \(\widehat {ACD} = \widehat {DCB}\)
\(\widehat {ACD} = \widehat {DCB}\)
Và ![]() \(\widehat B = \widehat C\) nên
\(\widehat B = \widehat C\) nên ![]() \(\widehat {ABE} = \widehat {ACD}\)
\(\widehat {ABE} = \widehat {ACD}\)
Xét tam giác BEA và tam giác CDA có:
![]() \(\widehat A\)chung
\(\widehat A\)chung
AB = AC (gt)
![]() \(\widehat {ABE} = \widehat {ACD}\)
\(\widehat {ABE} = \widehat {ACD}\)
Suy ra tam giác BEA bằng với tam giác CDA (theo trường hợp g-c-g)
Suy ra BE = CD và AD = AE (cặp cạnh tương ứng)
b, Có ![]() \(\Delta BEA = \Delta CDE \Rightarrow \widehat {AEB} = \widehat {ADC}\)
\(\Delta BEA = \Delta CDE \Rightarrow \widehat {AEB} = \widehat {ADC}\)
Xét tam giác AID và tam giác AIE có:
![]() \(\begin{array}{l} \widehat {AEB} = \widehat {ADC}\\ AD = AE \end{array}\)
\(\begin{array}{l} \widehat {AEB} = \widehat {ADC}\\ AD = AE \end{array}\)
AI chung
Suy ra tam giác AID bằng tam giác AIE (theo trường hợp c-g-c)
Suy ra ![]() \(\widehat {AMB} = \widehat {AMC}\)(hai góc tương ứng)
\(\widehat {AMB} = \widehat {AMC}\)(hai góc tương ứng)
Lại có ![]() \(\widehat {AMB} + \widehat {AMC} = {180^0} \Rightarrow \widehat {AMB} = {90^0}\)
\(\widehat {AMB} + \widehat {AMC} = {180^0} \Rightarrow \widehat {AMB} = {90^0}\)
Suy ra hai tam giác AMB và AMC là hai tam giác vuông cân
7. Bài tập về tam giác vuông cân
Trước khi đi trực tiếp đến giải các bài tập liên quan đến tam giác vuông cân các bạn tham khảo một số dạng bài cơ bản và phổ biến nhất:
Dạng 1: Nhận biết một tam giác cho trước bất kỳ là tam giác cân, tam giác đều hoặc vuông cân
Cách giải: Dựa theo dấu hiệu nhận biết / cách chứng minh từng loại tam giác. Trước hết nên phán đoán để tìm ra cách giải nhanh nhất
Dạng 2: Chứng minh các tính chất của tam giác được cho ví dụ là: tính độ dài của cạnh, độ dài của góc, chứng minh sự bằng nhau của tam giác,....
Cách giải: Để giải dạng toán này, bạn cần vận dụng kiến thức là tính chất của các tam giác này cùng với dữ liệu đề bài là có thể tìm ra đáp án.
Bài 1:
a. Một tam giác cân có một góc là 800. Số đo của hai góc còn lại là bao nhiêu?
b. Một tam giác cân có một góc là 1000. Số đo của hai góc còn lại là bao nhiêu?
Bài 2: Cho tam giác ABC nhọn (AB < AC), gọi M là trung điểm của đoạn thẳng BC. Kẻ AH ⊥ AM (H ∈ AM). Trên tia đối của tia AM lấy điểm N sao cho AN = 2MH. Chứng minh rằng BN = AC.
Bài 3: Cho tam giác ABC vuông tại A. Trên cạnh AC lấy điểm E sao cho ![]() \(\widehat {EBC} = 2\widehat {ABE}\). Trên tia BE lấy điểm M sao cho EM = BC. So sánh hai góc
\(\widehat {EBC} = 2\widehat {ABE}\). Trên tia BE lấy điểm M sao cho EM = BC. So sánh hai góc ![]() \(\widehat {MBC},\widehat {BMC}\).
\(\widehat {MBC},\widehat {BMC}\).
Bài 4: Cho tam giác ABC cân tại A có góc B = 60 độ và AB = 5 cm. Tia phân giác của góc B cắt AC tại D. Kẻ DE vuông góc với BC (E thuộc BC).
a. Chứng minh tam giác ABD = tam giác EBD.
b. Chứng minh tam giác ABE là tam giác đều.
c. Chứng minh tam giác AEC là tam giác cân.
d. Tính độ dài cạnh AC.
Bài 5: Cho tam giác ABC có số đo góc A là 1200. Trên đờng phân giác AD của góc A lấy điểm I. Trên tia đối của AC và AB lấy điểm E và F sao cho AE = AF = AI.
a. Chứng minh rằng: AB và AC là trung trực của IE và IF.
b. Chứng minh rằng tam giác IEF đều.
c. Chứng minh rằng AI ⊥ EF.
Bài 6: Cho tam giác ABC cân tại A có góc A < 900. Kẻ BD vuông góc với AC. Trên AB lấy điểm E sao cho AE = AD. Chứng minh rằng:
a) DE // BC
b) CE vuông góc với AB.
Bài 7: Cho tam giác ABC có BC < BA. Qua C kẻ đường thẳng vuông góc với tia phân giác BE của góc ABC và đường thẳng này cắt BE tại F và cắt trung tuyến BD tại G. Chứng minh rằng đoạn thẳng EG bị đoạn thẳng DF chia làm hai phần bằng nhau.
Bài 8
Hãy cho biết cần thêm điều kiện gì để
a, Tam giác vuông trở thành tam giác vuông cân
b, Tam giác cân trở thành tam giác vuông cân
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:












 Lớp 2
Lớp 2
 Lớp 4
Lớp 4
 Lớp 5
Lớp 5
 Thi vào 6
Thi vào 6
 Lớp 6
Lớp 6
 Lớp 7
Lớp 7
 Lớp 9
Lớp 9









