Bài tập GTLN - GTNN của Số Phức Tài liệu ôn tập môn Toán lớp 12
Với mong muốn đem đến cho các bạn đọc có thêm nhiều tài liệu học tập môn Toán lớp 12, Eballsviet.com giới thiệu Bài tập GTLN - GTNN của Số phức.
Bài tập giá trị lớn nhất và giá trị nhỏ nhất (viết tắt là GTLN – GTNN hoặc min – max) của biểu thức số phức là một dạng toán vận dụng cao thường gặp trong các đề thi thử THPT Quốc gia môn Toán trong những năm gần đây. Đây là dạng toán ít được đề cập đến trong sách giáo khoa Giải tích 12, do đó đã gây không ít bỡ ngỡ và khó khăn cho các bạn học sinh trong quá trình tiếp cận và tìm hướng giải quyết bài toán. Nội dung chi tiết mời các bạn cùng tham khảo và tải tại đây.
Bài tập GTLN - GTNN của Số Phức
https://toanmath.com/
GTLN - GTNN CỦA MÔĐUN SỐ PHỨC
A. BÀI TOÁN CỰC TRỊ CỦA SỐ PHỨC
I. CÁC BÀI TOÁN QUI VỀ BÀI TOÁN TÌM GIÁ TRỊ LỚN NHẤT, NHỎ NHẤT CỦA HÀM
MỘT BIẾN
1. PHƯƠNG PHÁP
Bài toán: Trong các số phức
z
thoả mãn điều kiện T. Tìm số phức z để biểu thức P đạt giá trị nhỏ
nhất, lớn nhất
Từ điều kiện T, biến đổi để tìm cách rút ẩn rồi thế vào biểu thức P để được hàm một biến.
Tìm giá trị lớn nhất (hoặc nhỏ nhất) tuỳ theo yêu cầu bài toán của hàm số một biến vừa tìm được.
II. CÁC BÀI TOÁN QUI VỀ BÀI TOÁN TÌM GIÁ TRỊ LỚN NHẤT, NHỎ NHẤT CỦA MỘT
BIỂU THỨC HAI BIẾN MÀ CÁC BIẾN THOẢ MÃN ĐIỀU KIỆN CHO TRƯỚC.
1. PHƯƠNG PHÁP:
Để giải được lớp bài toán này, chúng tôi cung cấp cho học sinh các bất đẳng thức cơ bản như: Bất đẳng
thức liên hệ giữa trung bình cộng và trung bình nhân, bất đẳng thức Bunhia- Cốpxki, bất đẳng thức hình
học và một số bài toán công cụ sau:
U
BÀI TOÁN CÔNG CỤ 1:
U
Cho đường tròn
()T
cố định có tâm I bán kính R và điểm A cố định. Điểm M di động trên đường
tròn
()T
. Hãy xác định vị trí điểm M sao cho AM lớn nhất, nhỏ nhất.
UGiải:
TH1: A thuộc đường tròn (T)
Ta có: AM đạt giá trị nhỏ nhất bằng 0 khi M trùng với A
AM đạt giá trị lớn nhất bằng 2R khi M là điểm đối xứng với A qua I
TH2: A không thuộc đường tròn (T)
Gọi B, C là giao điểm của đường thẳng qua A,I và đường tròn (T);
Giả sử AB < AC.
+) Nếu A nằm ngoài đường tròn (T) thì với điểm M bất kì trên (T), ta có:
AM AI IM AI IB AB≥− =−=
.
Đẳng thức xảy ra khi
MB≡
AM AI IM AI IC AC≤+ =+=
.
Đẳng thức xảy ra khi
MC≡
+) Nếu A nằm trong đường tròn (T) thì với điểm M bất kì trên (T),
ta có:
AM IM IA IB IA AB≥ −=−=
.
Đẳng thức xảy ra khi
MB≡
AM AI IM AI IC AC≤+ =+=
.
Đẳng thức xảy ra khi
MC≡
Vậy khi M trùng với B thì AM đạt gía trị nhỏ nhất.
Vậy khi M trùng với C thì AM đạt gía trị lớn nhất.
U
BÀI TOÁN CÔNG CỤ 2:
U
Cho hai đường tròn
1
()T
có tâm I, bán kính RR
1
R; đường tròn
2
()T
có tâm J, bán kính RR
2
R. Tìm vị trí
của điểm M trên
1
()T
, điểm N trên
2
()T
sao cho MN đạt giá trị lớn nhất, nhỏ nhất.
https://toanmath.com/
UGiải:
Gọi d là đường thẳng đi qua I, J;
d cắt đường tròn
1
()T
tại hai điểm phân biệt A, B (giả sử JA > JB) ; d cắt
2
()T
tại hai điểm phân biệt C, D
( giả sử ID > IC).
Với điểm M bất khì trên
1
()T
và điểm N bất kì trên
2
()T
.
Ta có:
12
MN IM IN IM IJ JN R R IJ AD≤+≤++=++=
.
Đẳng thức xảy ra khi M trùng với A và N trùng với D
12
MN IM IN IJ IM JN IJ R R BC≥ − ≥ − − = −+ =
.
Đẳng thức xảy ra khi M trùng với B và N trùng với C.
Vậy khi M trùng với A và N trùng với D thì MN đạt
giá trị lớn nhất.
khi M trùng với B và N trùng với C thì MN đạt giá trị nhỏ nhất.
U
BÀI TOÁN CÔNG CỤ 3:
U
Cho hai đường tròn
()
T
có tâm I, bán kính R; đường thẳng
∆
không có điểm chung với
()T
. Tìm vị
trí của điểm M trên
()T
, điểm N trên
∆
sao cho MN đạt giá trị nhỏ nhất.
UGiải:
Gọi H là hình chiếu vuông góc của I trên d
Đoạn IH cắt đường tròn
()T
tại J
Với M thuộc đường thẳng
∆
, N thuộc đường tròn
()T
, ta có:
MN IN IM IH IJ JH const≥ − ≥ −= =
.
Đẳng thức xảy ra khi
;M HN I≡≡
Vậy khi M trùng với H; N trùng với J thì MN đạt giá trị nhỏ nhất.
B – BÀI TẬP
Câu 1. Trong các số phức thỏa mãn điều kiện
3 2.
ziz i+ = +−
Tìm số phức có môđun nhỏ nhất?
A.
12
55
zi=−+
. B.
12
55
zi= −
. C.
12zi=−+
. D.
12zi= −
.
Câu 2. Trong các số phức
z
thỏa mãn
24 2z izi−− = −
. Số phức
z
có môđun nhỏ nhất là
A.
32zi= +
B.
1zi=−+
C.
22zi=−+
D.
22zi= +
Câu 3. Cho số phức
z
thỏa mãn
1−= −z zi
. Tìm mô đun nhỏ nhất của số phức
w2 2= +−zi
.
A.
32
2
. B.
3
2
. C.
32
. D.
3
22
.
Câu 4. Cho số phức
z
thỏa mãn
34 1zi−− =
. Tìm giá trị nhỏ nhất của
z
.
A.
6
. B.
4
. C.
3
. D.
5
.
https://toanmath.com/
Câu 5. Cho hai số phức
1
z
,
2
z
thỏa mãn
1
352zi−+=
và
2
12 4iz i−+ =
. Tìm giá trị lớn nhất của biểu
thức
12
23T iz z= +
.
A.
313 16+
. B.
313
. C.
313 8+
. D.
313 2 5+
.
Câu 6. Trong các số phức
z
thỏa mãn điều kiện
23 12z iz i+ − = +−
, hãy tìm phần ảo của số phức có
môđun nhỏ nhất?
A.
10
13
. B.
2
5
. C.
2−
. D.
2
13
−
.
Câu 7. Xét các số phức
1
34zi= −
và
2
2z mi= +
,
( )
m∈
. Giá trị nhỏ nhất của môđun số phức
2
1
z
z
bằng?
A.
2
5
. B.
2
. C.
3
. D.
1
5
.
Câu 8. Số phức
z
nào sau đây có môđun nhỏ nhất thỏa
| || 3 4|zz i= −+
:
A.
3
2
2
zi=−−
. B.
7
3
8
zi= −
.
C.
3
2
2
zi= +
.
D.
3–4zi= −
.
Câu 9. Có tất cả bao nhiêu giá trị nguyên của
m
để có đúng hai số phức
z
thỏa mãn
( )
18zm i− − +=
và
1 23
z iz i−+ = − +
.
A.
66
. B.
130
. C.
131
. D.
63
.
Câu 10. Cho các số phức
z
thoả mãn
2=z
. Đặt
( )
12 12= + −+w iz i
. Tìm giá trị nhỏ nhất của
w
.
A.
2
. B.
35
. C.
25
. D.
5
.
Câu 11. Cho số phức
z
thỏa mãn
11zi−− =
, số phức
w
thỏa mãn
23 2wi−− =
. Tìm giá trị nhỏ nhất
của
zw−
.
A.
17 3
+
B.
13 3+
C.
13 3−
D.
17 3−
Câu 12. Cho số phức
( )
,
12
mi
zm
mm i
−+
= ∈
−−
. Tìm môđun lớn nhất của
.z
A. 2. B. 1. C. 0. D.
1
2
.
Câu 13. Cho số phức
z
thỏa mãn
13z izi+− = −
. Tính môđun nhỏ nhất của
zi−
.
A.
35
10
. B.
45
5
. C.
35
5
. D.
75
10
.
Câu 14. Cho số phức
z
thoả mãn
34 5zi−− =
. Gọi
M
và
m
là giá trị lớn nhất và giá trị nhỏ nhất của
biểu thức
22
2P z zi
=+ −−
. Tính môđun của số phức
.w M mi= +
A.
2 309w
=
. B.
2315w =
. C.
1258w =
. D.
3 137w =
.
Câu 15. Cho số phức
z
thỏa mãn
12 3zi−+ =
. Tìm môđun lớn nhất của số phức
2.zi−
A.
+26 8 17
. B.
−26 4 17
. C.
+26 6 17
. D.
−26 6 17
.
Câu 16. Giả sử
1
z
,
2
z
là hai trong số các số phức
z
thỏa mãn
21iz i+ −=
và
12
2zz−=
. Giá trị lớn
nhất của
12
zz+
bằng
Chia sẻ bởi: 
Trịnh Thị Thanh
Trịnh Thị Thanh Liên kết tải về
Bài tập GTLN - GTNN của Số Phức 1,4 MB Tải về
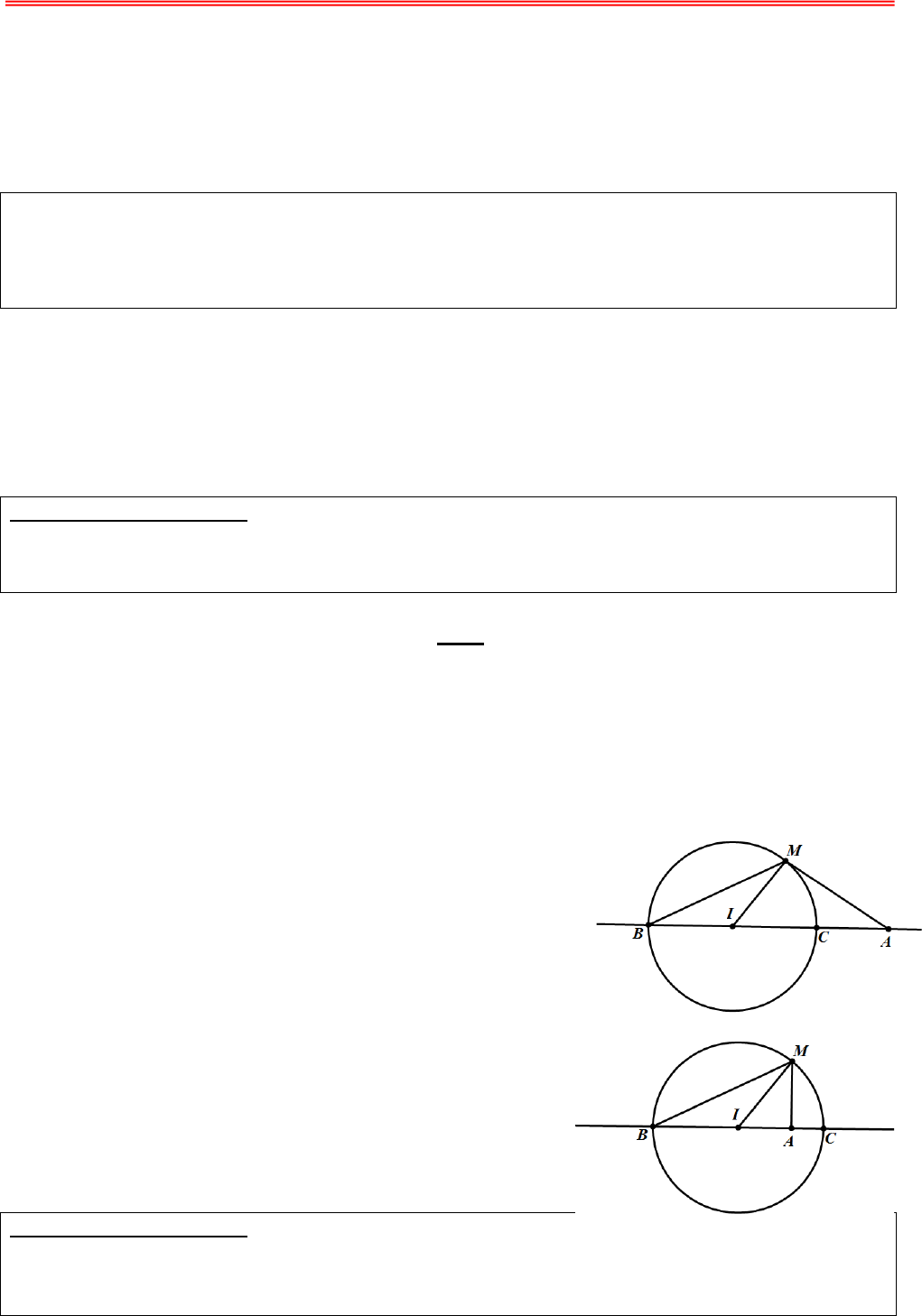
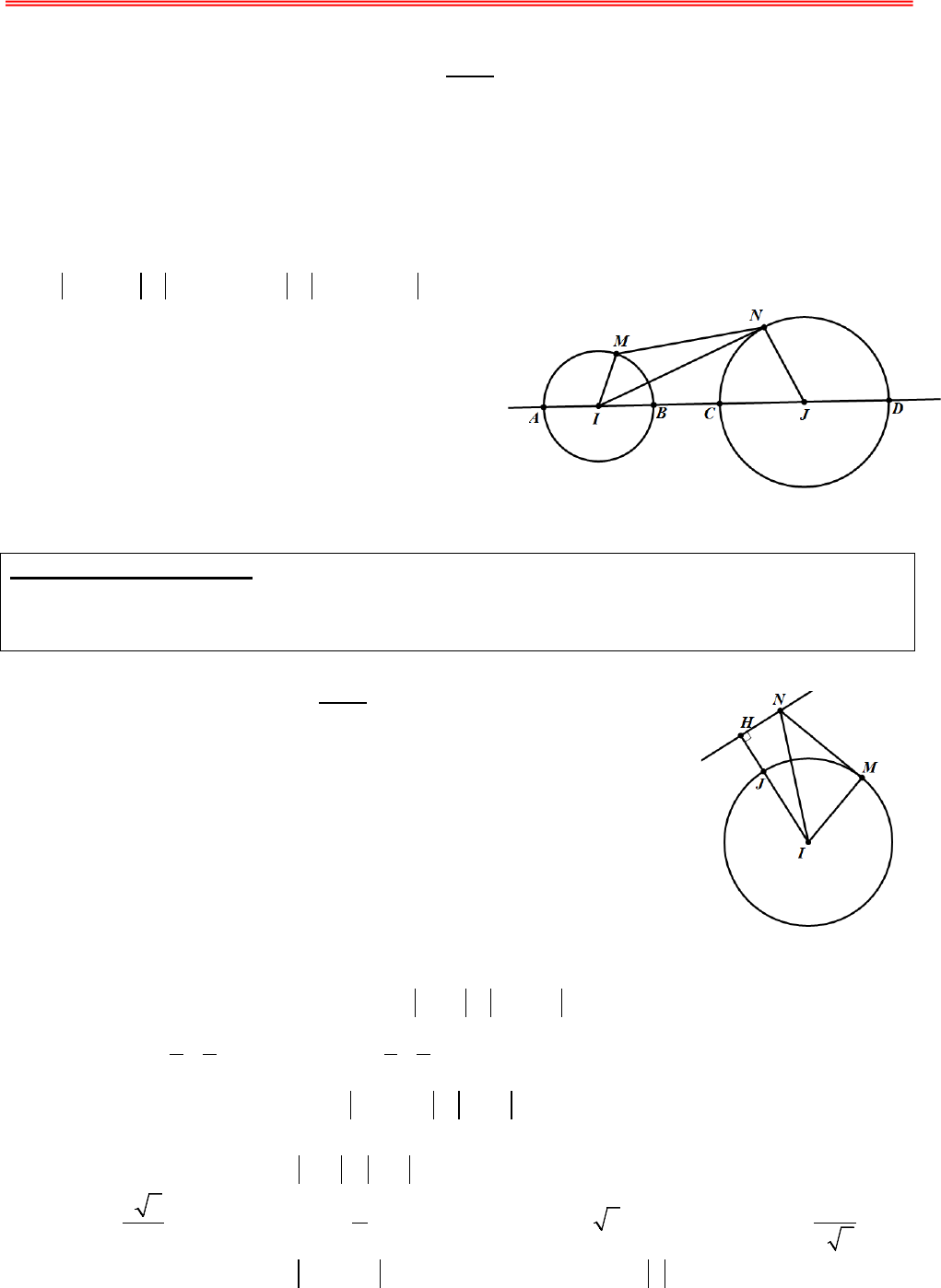
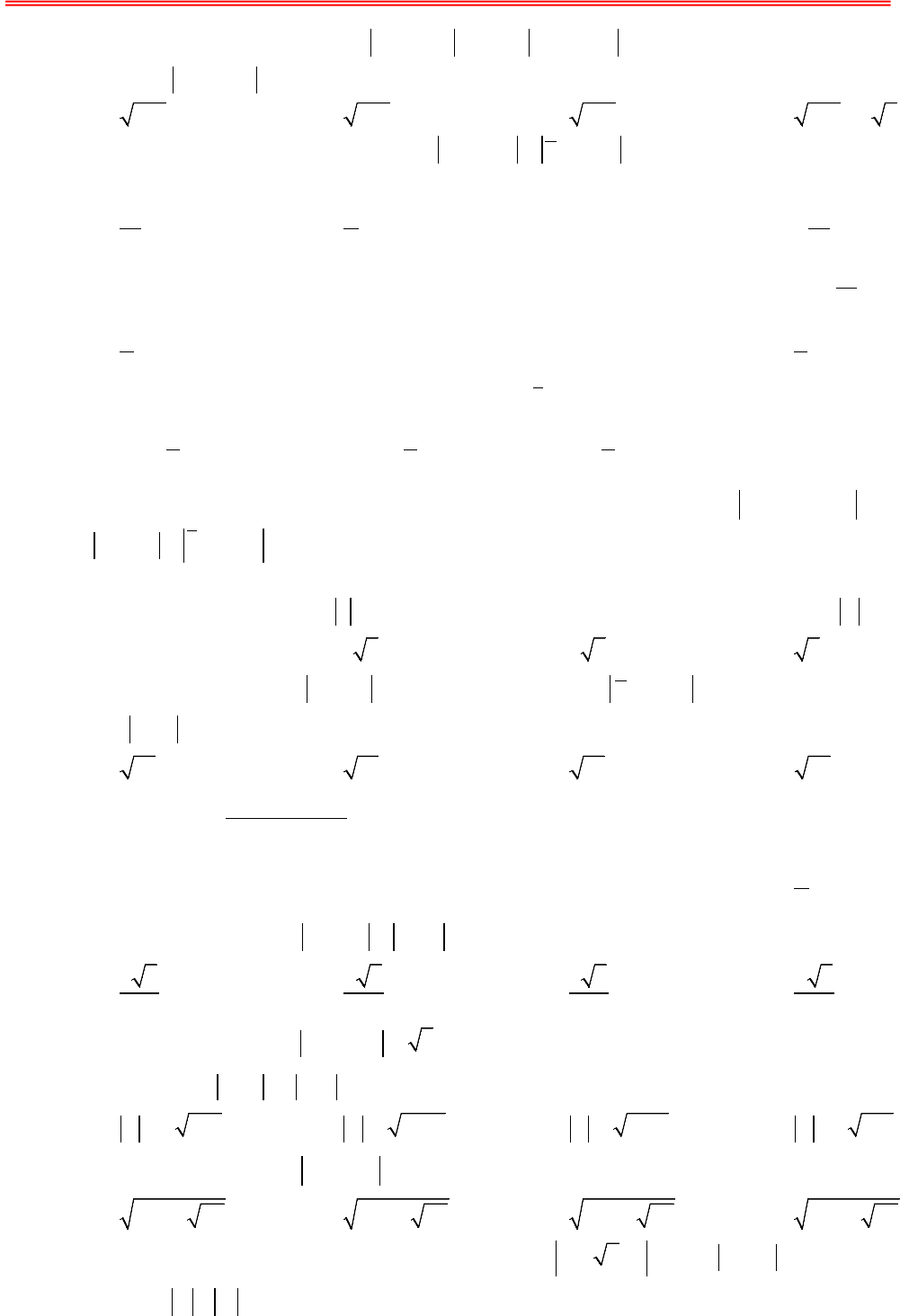
Có thể bạn quan tâm
-
Văn mẫu lớp 9: Dàn ý Nghị luận về hiện tượng nói tục chửi thề của học sinh
-
Bộ câu hỏi thi Tìm hiểu dịch vụ công trực tuyến năm 2019
-
Văn mẫu lớp 7: Đoạn văn ghi lại cảm xúc về bài thơ Con chim chiền chiện
-
Phân biệt phản xạ có điều kiện và phản xạ không điều kiện
-
Bộ đề thi giữa học kì 2 lớp 7 năm 2023 - 2024 (Sách mới)
-
Thuyết minh về cách làm một món ăn mà em yêu thích (Dàn ý + 18 mẫu)
-
Đoạn văn tiếng Anh viết về hệ thống giáo dục ở Việt Nam (Dàn ý + 10 Mẫu)
-
Tập làm văn lớp 4: Tả cây cam mà em yêu thích
-
Mẫu kế hoạch công tác chủ nhiệm năm học 2024 - 2025 (Cách viết + 12 Mẫu)
-
Hợp đồng mua bán máy móc, thiết bị
Xác thực tài khoản!
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
Số điện thoại chưa đúng định dạng!
Sắp xếp theo
