Thủ thuật tính đạo hàm của một hàm cơ bản bằng Casio Tài liệu ôn tập môn Toán lớp 11
Thủ thuật tính đạo hàm của một hàm cơ bản bằng Casio là tài liệu rất hữu ích mà Eballsviet.com muốn giới thiệu đến các bạn học sinh lớp 11 cùng tham khảo.
Tài liệu giới thiệu một số thủ thuật tính nhanh đạo hàm các hàm số cơ bản bằng cách sử dụng máy tính Casio. Các hàm được giới thiệu gồm: Tính đạo hàm của một đa thức; Tính đạo hàm của một phân thức; Tính đạo hàm của hàm 1 căn; Tính đạo hàm của hàm 2 căn. Sau đây là nội dung chi tiết, mời bạn đọc cùng tham khảo và tải tài liệu tại đây.
Thủ thuật tính đạo hàm của một hàm cơ bản bằng Casio
Thủ thuật tính đạo hàm của một số hàm cơ bản bằng casio
THỦ THUẬT TÍNH ĐẠO HÀM
CỦA MỘT SỐ HÀM CƠ BẢN BẰNG CASIO
Nguyễn Minh Tuấn – THPT Bình Minh
Tham khảo thêm tại blog Casioer team:
https://drive.google.com/file/d/0BzdhLKdFcFCvUHh6TnFpdnFadTg/view?usp=sharing
A. TÍNH ĐẠO HÀM CỦA MỘT ĐA THỨC.
Để tận dụng tốt phím
d
dx
ở trong máy tính trong việc tình đạo hàm ta sẽ cî cách để
tình đạo hàm của các hàm số đa thức như sau:
Bước 1: Nhập vào máy
xX
d
fx
dx
Bước 2:
CALC X 1000
sau đî ta tiến hành biểu diễn số đî qua
X
và thế là
xong!
Ví dụ 1: Tính đạo hàm của hàm số sau:
23
3 2 2
f x x 3x 2 x 1 x 2 x x 1 x 2
Bước 1: Nhập vào máy:
23
3 2 2
xX
d
X 3X 2 X 1 X 2 X X 1 X 2
dx
Bước 2:
CALC X 1000
ta được kết quả:
8036042017
Tuy nhiên đây là kết quả tính của máy VINACAL còn máy
VN sẽ ra kết quả khác hình ảnh như sau:
Đî là hënh ảnh kết quả tëm được của máy Casio 570 Vn. Cái đuïi của kết quả là 36 còn của
VINACAL là 17. Bằng thực nghiệm ta thấy kết quả 17 của máy VINACAL là đúng. Những
bạn nào đang dùng VN hay dùng máy CASIO thë đừng quá quan trọng lỗi này, ta vẫn có
thể khắc phục bằng cách sau:
Sau khi tëm được kết quả của
2
x
ta sẽ
CALC X 0
để tìm hệ số tự do, sau đî trừ đi hệ số
tự do rồi
CALC X 1
để tìm hệ số của X thế là kết quả là đúng. Ngoài ra khi bậc của đạo
hàm quá cao thì ta vẫn có thể dùng cách
CALC X 0.001
để tìm lần lượt các hệ số từ bậc
nhỏ đến lớn.
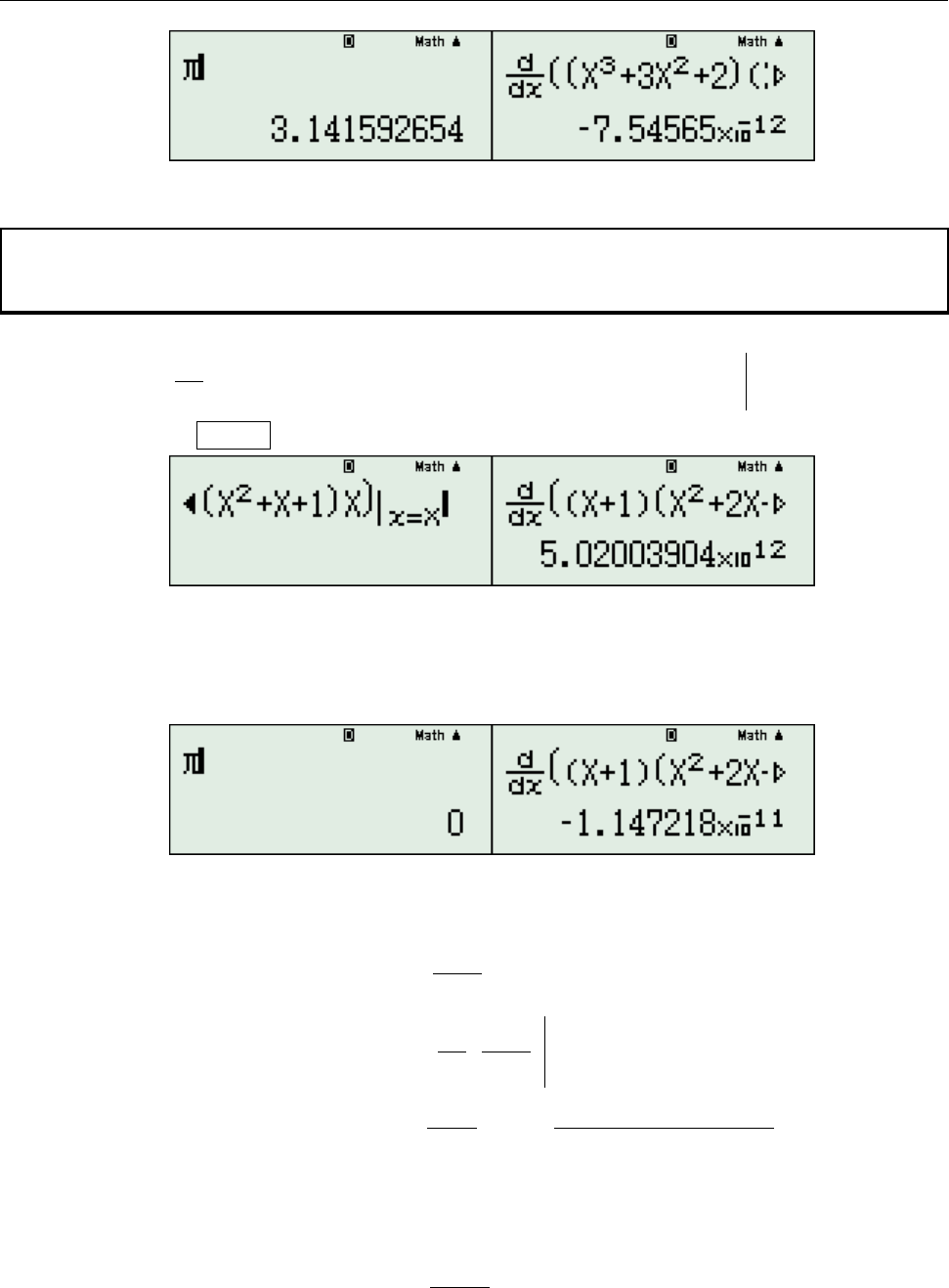
+ Tiến hành rút gọn ta được kết quả như sau:
32
8036042017 8x 36x 42x 17
+ Ghi vào sau:
32
8X 36X 42X 17, CALC X
ta được:
Thủ thuật tính đạo hàm của một số hàm cơ bản bằng casio
Vậy kết quả tình đạo hàm là đúng!
Ví dụ 2: Tính đạo hàm của hàm số sau:
2
22
f x x 1 x 2x 3 x 1 x 2 x x 1 x
Bước 1: Nhập vào máy:
2
22
xX
d
X 1 X 2X 3 X 1 X 2 X X 1 X
dx
Bước 2:
CALC X 1000
ta được kết quả:
12
5.02003904 10
+ Tiến hành rút gọn ta được kết quả như sau:
12 4 3 2
5.02003904 10 5x 20x 39x 40x 21
+ Ghi vào sau:
4 3 2
5X 20X 39X 40X 21,CALC X
ta được kết quả bằng 0 tức là
kết quả tình đúng!
B. TÍNH ĐẠO HÀM CỦA MỘT PHÂN THỨC.
Giả sử ta phải tình đạo hàm của hàm
fx
y
gx
thì gồm những bước sau:
Bước 1: Nhập vào máy:
2
xX
fx
d
gx
dx g x
Do công thức tình đạo hàm của hàm
2
f x f' x g x g' x f x
y y'
gx
gx
nên ta phải
nhân vào trước biểu thức
2
gx
để làm mất mẫu.
Bước 2: Sau đî tiến hành rút gọn ta được tử của
y'
là đa thức
hx
. Cuối cùng
chỉ việc ghi vào bài làm là
2
hx
y'
gx
, và thế là xong!
Thủ thuật tính đạo hàm của một số hàm cơ bản bằng casio
Ví dụ 1: Tính đạo hàm của hàm số sau:
3 2 2
2
x x x x 1 x 2
fx
x1
Bước 1: Nhập vào máy biểu thức sau:
3 2 2
2
2
2
xX
X X X X 1 X 2
d
X1
dx X 1
Bước 2:
CALC X 1000
ta được kết quả
12
2.000005 10
+ Tiến hành rút gọn biểu thức trên ta được kết quả:
12 4 2
2.000005 10 2x 5x 1
+ Ghi vào sau:
42
2 X 5X 1
,
CALC X
được kết quả:
Vậy kết quả tình đạo hàm là đúng!
Như vậy kết quả của bài toán là:
3 2 2
42
2
2
2
x x x x 1 x 2
2x 5x 1
f x f ' x
x1
x1
Ví dụ 2: Tính đạo hàm của hàm số sau:
4
3
x1
fx
2x 4
Nhận xét: Theo như các bước làm ở trên, ta sẽ nhập vào màn hình biểu thức
4
6
3
xX
x1
d
2x 4
dx
2x 4
Nhưng tuy nhiên với phương pháp
CALC X 1000
ta thì bắt
đầu có vấn đề vì máy tính chỉ tính chính xác trong khoảng
15 15
10 ;10
mà
6
x
đã lên tới
18
10
, cho nên cách này làm chắc chắn thất bại. Mà cho dù bạn nào có
CALC X 100
để
giảm số mũ thë chắc chắn cũng sai vë bài này hệ số rất lớn! Do đî ta làm như sau, nhập vào
máy biểu thức sau
4
4
3
xX
x1
d
2x 4
dx
2x 4
. Mënh đoán rằng sau khi tôi viết thế này
chắc có nhiều bạn sẽ đặt câu hỏi là tại sau dưới mẫu là
4
2x 4
mà không phải là
6
2x 4
theo như cïng thức tình đạo hàm. Sau đây là chứng minh:
+ Ta có:
n n n n 1
2
n 2n
n
g' x .h x g x h x ' g' x h x g x n.hx x .h' x
gx
f x f' x
h x h x
hx
n1
2n n 1
h x g' x .h x ng x .h' x
g' x .h x n.g x .h' x
h x h x
Chia sẻ bởi: 
Trịnh Thị Thanh
Trịnh Thị Thanh Liên kết tải về
Link Download chính thức:
Thủ thuật tính đạo hàm của một hàm cơ bản bằng Casio Download
Có thể bạn quan tâm
-
Giáo án Toán lớp 1 (Sách mới) - Giáo án Toán lớp 1 (trọn bộ 5 sách)
-
Tuyển tập đề thi học sinh giỏi môn Toán lớp 3
-
Thuyết minh về Thành Cổ Loa (2 Dàn ý + 5 mẫu)
-
Bộ tranh tô màu chủ đề gia đình cho bé
-
Văn mẫu lớp 10: Phân tích tác phẩm Hiền tài là nguyên khí của quốc gia (2 Dàn ý + 10 Mẫu)
-
Những vần thơ hay - Tuyển tập những bài thơ hay
-
Văn mẫu lớp 9: Nghị luận về hiện tượng học tủ, học vẹt
-
File luyện viết chữ in hoa - Mẫu chữ hoa cho học sinh Tiểu học
-
Đề kiểm tra học kì II môn Toán lớp 1
-
Văn mẫu lớp 7: Phân tích bài Ngẫu nhiên viết nhân buổi mới về quê
Sắp xếp theo
