Tài liệu dạy thêm Toán 11 sách Kết nối tri thức với cuộc sống Tài liệu dạy thêm Toán 11 (Tập 1)

Giới thiệu Tải về Bình luận

Tài liệu dạy thêm Toán 11 Kết nối tri thức với cuộc sống là tài liệu tham khảo hữu ích nhằm giúp thầy cô giáo chuẩn bị tốt hơn cho tiết dạy của mình.

Dạy thêm Toán 11 Kết nối tri thức được biên soạn rất chi tiết theo từng bài học của cả năm. Tài liệu dạy thêm Toán 11 được thiết kế đầy đủ lý thuyết, các dạng bài tập trọng tâm có đáp án kèm theo. Hi vọng giáo án dạy thêm Toán lớp 11 này sẽ góp phần hỗ trợ các thầy cô giáo giảng dạy tốt hơn môn Toán. Vậy sau đây là trọn bộ Tài liệu dạy thêm Toán 11 Kết nối tri thức, bạn đọc cùng tham khảo và tải tài liệu tại đây.

Tài liệu dạy thêm Toán 11 Kết nối tri thức

CHƯƠNG 1: HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC

BÀI 1: GÓC LƯỢNG GIÁC

A. TÓM TẮT KIẾN THỨC CƠ BẢN CẦN NẮM.

1. Góc lượng giác

Khái niệm góc lượng giác

Khi xét chuyển động quay của một tia O m quanh gốc O của nó tính từ vị trí ban đầu O a theo một chiều cố định, người ta quy ước chiều quay ngược chiều kim đồng hồ là chiều dương và chiều quay cùng chiều kim đồng hồ là chiều âm.

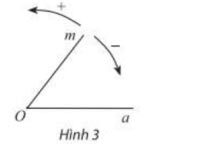
Một vòng quay theo chiều dương tương ứng với góc quay $-360^{\circ}$ $-360^{\circ}$, một vòng quay theo chiều âm tương ứng với góc quay $-360^{\circ}$ $-360^{\circ}$. Khi tia Om quay:

- nửa vòng theo chiều dương thì ta nói O m quay góc $\frac{1}{2} \cdot 360^{\circ}=180^{\circ};$ $\frac{1}{2} \cdot 360^{\circ}=180^{\circ};$

- $\frac{1}{6}$ $\frac{1}{6}$ vòng theo chiều dương thì ta nói Om quay góc $\frac{1}{6} \cdot 360^{\circ}=60^{\circ};$ $\frac{1}{6} \cdot 360^{\circ}=60^{\circ};$

- $\frac{5}{4}$ $\frac{5}{4}$ vòng theo chiều âm thì ta nói O m quay góc $\frac{5}{4} \cdot\left(-360^{\circ}\right)=-450^{\circ}.$ $\frac{5}{4} \cdot\left(-360^{\circ}\right)=-450^{\circ}.$

Cho hai tia $\mathrm{Oa}, \mathrm{Ob}.$ $\mathrm{Oa}, \mathrm{Ob}.$

- Nếu một tia O m quay quanh gốc O của nó theo một chiều cố định bắt đầu từ vị trí tia O a và dừng ở vị trí tia O b thì ta nói tia O m quét một góc lượng giác có tia đầu O a, tia cuối O b, kí hiệu $(\mathrm{Oa}, \mathrm{Ob}).$ $(\mathrm{Oa}, \mathrm{Ob}).$

- Khi tia O m quay một góc $\alpha$ $\alpha$, ta nói số đo của góc lượng giác (O a, O b) bằng $\alpha$ $\alpha$, kí hiệu $\mathrm{sđ}(\mathrm{Oa}, \mathrm{Ob})=\alpha.$ $\mathrm{sđ}(\mathrm{Oa}, \mathrm{Ob})=\alpha.$

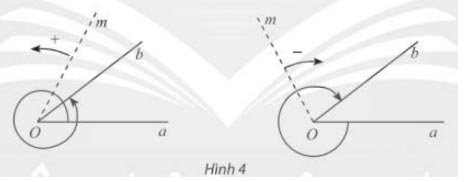
Chú ý: Với hai tia O a và O b cho trước, có vô số góc lượng giác tia đầu O a và tia cuối O b. Ta dùng chung kí hiệu (Oa, Ob) cho tất cả các góc lượng giác này.

Nhận xét: Số đo của các góc lượng giác có cùng tia đầu O a và tia cuối O b sai khác nhau một bội nguyên của $360^{\circ}$ $360^{\circ}$ nên có công thức tổng quát là:

$sđ (\mathrm{Oa}, \mathrm{Ob})=\alpha^{\circ}+k 360^{\circ}(k \in \mathrm{Z}$ $sđ (\mathrm{Oa}, \mathrm{Ob})=\alpha^{\circ}+k 360^{\circ}(k \in \mathrm{Z}$), thường viết là $(O a, O b)=\alpha^{\circ}+k 360^{\circ}$ $(O a, O b)=\alpha^{\circ}+k 360^{\circ}$ với $\alpha^{\circ}$ $\alpha^{\circ}$ là số đo của một góc lượng giác bất kì có tia đầu O a và tia cuối O b.

Hệ thức Chasles (Sa-lơ)

Ta thừa nhận hệ thức sau về số đo của góc lượng giác, gọi là hệ thức Chasles:

Với ba tia O a, O b và O c bất kì, ta có

$(O a, O b)+(O b, O c)=(O a, O c)+k 360^{\circ}(k \in Z)$ $(O a, O b)+(O b, O c)=(O a, O c)+k 360^{\circ}(k \in Z)$

2. Đơn vị radian

-Trên đường tròn bán kính R tuỳ ý, góc ở tâm chắn một cung có độ dài đúng bằng R được gọi là một góc có số đo 1 radian (đọc là 1 ra-đi-an, viết tắt là 1 rad).

...........

Tải file tài liệu để xem trọn bộ Tài liệu dạy thêm Toán 11 sách Kết nối tri thức

Chia sẻ bởi: