Đề thi học sinh giỏi lớp 12 THPT tỉnh Hải Dương năm học 2011 - 2012 môn Toán (Vòng 2) - Có đáp án Sở GD&ĐT Hải Dương

Tải về Bình luận

SỞ GIÁO DỤC VÀ ĐÀO TẠO
HẢI DƯƠNG

(ĐỀ THI CHÍNH THỨC)

KÌ THI CHỌN HỌC SINH GIỎI TỈNH
LỚP 12 THPT NĂM HỌC 2011 - 2012

ĐỀ THI MÔN: TOÁN - VÒNG 2

Thời gian làm bài: 180 phút (không kể thời gian giao đề)

Câu 1 (2 điểm)

a) Cho hàm số y = x² + 2mx - 3m và hàm số y = -2x + 3. Tìm m để đồ thị các hàm số đó cắt nhau tại hai điểm phân biệt và hoành độ của chúng đều dương.

b) Giải bất phương trình:

Câu 2 (2 điểm)

a) Giải phương trình:

b) Giải phương trình:

Câu 3 (2 điểm)

a) Trong mặt phẳng tọa độ Oxy cho điểm M(1; 4). Đường thẳng d qua M, d cắt trục hoành tại A (hoành độ của A dương), d cắt trục tung tại B (tung độ của B dương). Tìm giá trị nhỏ nhất của diện tích tam giác OAB.

b) Trong mặt phẳng tọa độ Oxy cho đường tròn (C): (x - 2)² + (y + 3)² = 9 và điểm A(1; -2). Đường thẳng Δ qua A, Δ cắt (C) tại M và N. Tìm giá trị nhỏ nhất của độ dài đoạn thẳng MN.

Câu 4 (3 điểm)

a) Chứng minh rằng tứ giác lồi ABCD là hình bình hành khi và chỉ khi AB² + BC² + CD² + DA² = AC² + BD²

b) Tìm tất cả các tam giác ABC thỏa mãn: 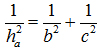(trong đó AB=c; AC=b; đường cao qua A là h_a).

Câu 5 (1 điểm)

Cho a, b, c là các số thực dương. Chứng minh rằng: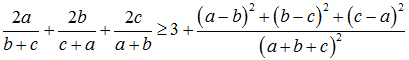
Đề thi học sinh giỏi lớp 12 THPT tỉnh Hải Dương năm học 2011 - 2012 môn Toán

Download tài liệu để xem thêm chi tiết

Chia sẻ bởi:

Nguyễn Thu Ngân

Tải về

Liên kết tải về

Đề thi học sinh giỏi lớp 12 THPT tỉnh Hải Dương năm học 2011 - 2012 môn Toán (Vòng 2) - Có đáp án 286 KB Tải về

Tìm thêm: Toán 12

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!