Eballsviet.com Học tập Lớp 12 Toán 12

Đề thi học sinh giỏi lớp 12 THPT tỉnh Hải Dương năm học 2011 - 2012 môn Toán (Vòng 1) - Có đáp án Sở GD&ĐT Hải Dương

Tải về Bình luận
  • 1

SỞ GIÁO DỤC VÀ ĐÀO TẠO
HẢI DƯƠNG

(ĐỀ THI CHÍNH THỨC)

KÌ THI CHỌN HỌC SINH GIỎI TỈNH
LỚP 12 THPT NĂM HỌC 2011 - 2012

ĐỀ THI MÔN: TOÁN - VÒNG 1

Thời gian làm bài: 180 phút (không kể thời gian giao đề)

Câu 1 (2 điểm)

1. Cho hàm số có đồ thị là (C) và điểm M tùy ý thuộc (C). Tiếp tuyến của (C) tại điểm M cắt hai tiệm cận tại A và B. Gọi I là giao điểm của hai tiệm cận. Chứng minh tam giác IAB có diện tích không phụ thuộc vị trí điểm M.

2. Tìm m để hàm số có cực đại.

Câu 2 (2 điểm)

1. Giải phương trình:

2. Giải hệ phương trình: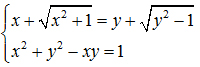

Câu 3 (2 điểm)

1. Chứng minh 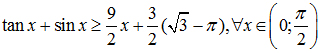. Từ đó suy ra trong mọi tam giác nhọn ABC ta có:

2. Tìm giá trị lớn nhất, nhỏ nhất của hàm số:

Câu 4 (3 điểm)

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA = A√3 và SA vuông góc với mặt phẳng đáy.

1. Mặt phẳng (P) đi qua điểm A và vuông góc với SC cắt SB, SC, SD lần lượt tại B’, C’, D’. Tính thể tích khối chóp S.AB’C’D’ theo a.

2. M và N là hai điểm thay đổi lần lượt thuộc các cạnh BC và DC sao cho góc MAN = 45o. Tìm giá trị lớn nhất và giá trị nhỏ nhất của thể tích khối chóp S.AMN.

Câu 5 (1 điểm)

Cho a, b, c là các số thực dương thỏa mãn a2 + b2 + c2 = 1. Chứng minh: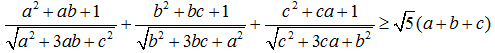

Download tài liệu để xem thêm chi tiết

Chia sẻ bởi: 👨 Nguyễn Thu Ngân
Liên kết tải về
Tìm thêm: Toán 12
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
👨

Tài liệu tham khảo khác

Chủ đề liên quan

Có thể bạn quan tâm

Xem thêm

Mới nhất trong tuần

Đóng
Chỉ thành viên Download Pro tải được nội dung này! Download Pro - Tải nhanh, website không quảng cáo! Tìm hiểu thêm
Mua Download Pro 79.000đ